Programación lineal
1. Definición de programación lineal
Se define como caso particular de la programación diferenciable con restricciones de desigualdad, cuando todas las funciones que intervienen son funciones lineales.
Ejemplo:
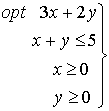
2. Propiedades de los óptimos en problemas lineales
- Todo problema de programación lineal es convexo y cóncavo, en consecuencia:
- Las condiciones de Kuhn-Tucker son necesarias y suficientes para mínimo y para máximo.
- No hay mínimos locales que no sean globales, ni máximos locales que no sean globales (ver teorema local-global).
- Un problema lineal no puede tener soluciones óptimas en puntos interiores del dominio (salvo en el caso de que la función objetivo sea constante).
- Tampoco puede ser óptimo un punto aislado de una arista, si no es óptima toda la arista o si ese punto no es vértice.
Conclusión:
- En un problema lineal las soluciones óptimas estarán en los vértices.
- Si dos vértices son máximos, todos los puntos de la arista que los une serán máximos. Del mismo modo, si dos vértices son mínimos, todos los puntos de la arista que los une serán mínimos.
3. Formulación canónica de los problemas lineales
Distinguiremos dos tipos de enunciado del problema lineal, según se trate de maximizar o de minimizar (Formulación canónica)
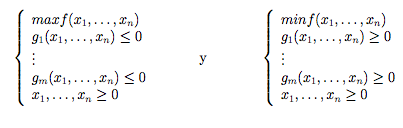
4. Multiplicadores de Kuhn-Tucker en programación lineal
Observemos que en los problemas de maximizar, las restricciones normalmente serán de la forma ≤ y en los de minimizar, de la forma ≥ . La explicación es inmediata: en los problemas de maximizar, beneficios por ejemplo, las restricciones serán del tipo ≤ pues reflejarán limitaciones (capacidad de trabajo limitada, capital inicial limitado, número de recursos limitado, etc...) y en los problemas de minimizar, costes por ejemplo, las restricciones serán del tipo ≥ pues reflejarán requerimientos (necesidad de abastecer un determinado número de clientes, necesidad de utilizar un determinado número de recursos, etc...)
Observemos que si deseamos aplicar las condiciones de Kuhn-Tucker a un problema lineal de maximizar, como las restricciones son ≤ corresponden al planteamiento que hemos hecho al hablar del problema con restricciones de desigualdad y en el óptimo los multiplicadores de K-T serán λi ≥ 0 ∀i. Si en cambio, deseamos aplicar las condiciones de K-T a un problema lineal de minimizar, en vez de multiplicar todas las restricciones por -1 para cambiar su sentido, podemos no hacerlo, sabiendo que en el óptimo los multiplicadores aparecerán con signo cambiado, es decir positivos λi ≥ 0 ∀i, en vez de negativos λi ≤ 0 ∀i. Por tanto:
Condiciones de Kuhn-Tucker en programación lineal

5. Dualidad
-
Sea (P)
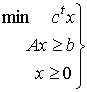 , entonces (D)
, entonces (D) 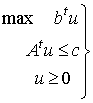
-
Sea (P)
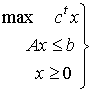 , entonces (D)
, entonces (D) 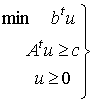
(siendo 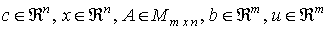 )
)
Propiedades de los problemas en dualidad
- Número de variables no negativas de (P) = Número de restricciones de desigualdad de (D)
- El dual del dual es el primal.
Teorema de dualidad:
Si uno de los dos programas lineales en dualidad posee un óptimo finito, también lo tiene el otro programa y ambos valores óptimos coinciden.
Observación:
Se puede comprobar que la formulación de las condiciones de Kuhn-Tucker coincide para ambos problemas primal y dual, resultando además que los multiplicadores de K-T asociados al punto óptimo del problema primal son justamente los valores de las variables no negativas del optimo del problema dual y viceversa.
Aquí se manifiesta la conveniencia de que en programación lineal, los multiplicadores de K-T se consideren siempre no negativos en el óptimo
Consecuencia:
Cuando el número de variables es más elevado que el de restricciones, resulta cómodo resolver el problema dual y, mediante los multiplicadores, deducir la solución óptima del problema primal.
Ejemplo:
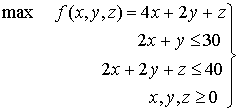 (P)
(P) 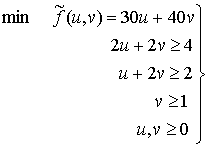 (D)
(D)
Es más cómodo resolver (D) porque tiene únicamente dos variables.
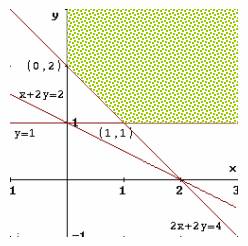
Puesto que 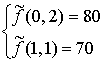 , el posible punto óptimo será el vértice (1,1).
, el posible punto óptimo será el vértice (1,1).
Nótese que el dominio no es compacto y que, por tanto, no puede aplicarse el teorema de Weierstrass. Sin embargo, es posible aplicar las condiciones de K-T al punto (1,1). Los multiplicadores obtenidos son los siguientes:
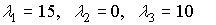
Así pues, se verifica que el punto (1,1) es mínimo global de (D). Además, podemos deducir que el punto óptimo del problema primal es (15,0,10) y que el valor máximo es 70, que coincide con el valor mínimo del problema dual.
