Optimizacion con restricciones de igualdad
1. Formulación del problema
Sea:
ƒ: ℜn → ℜ diferenciable
gi: ℜn → ℜ i = 1…m diferenciables
b1…bm ∈ ℜ
Un problema de optimización con restricciones de igualdad se formula:
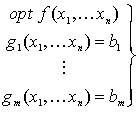
Ejemplo y representación gráfica
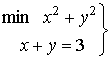 (n=2, m=1)
(n=2, m=1)
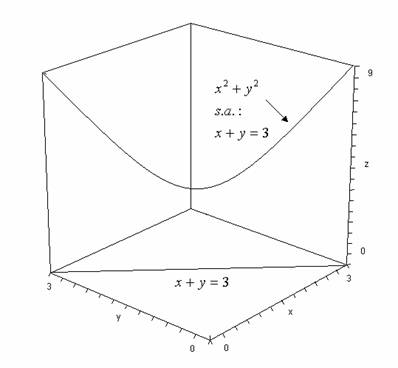
Nota:
- Las restricciones de tipo igualdad no establecen fronteras al conjunto de las soluciones factibles del programa, sino que reducen las dimensiones del espacio donde el programa está definido.
- Los óptimos que obtendremos serán “débiles” en el sentido de que una pequeña variación en las restricciones hará que dejen de ser óptimos. Por este motivo los llamaremos óptimos condicionados o restringidos.
2. Resolución de un problema de optimización con restricciones de igualdad
Métodos:
i. Resolución gráfica por curvas de nivel
Siempre que sea posible será muy cómodo dibujar las curvas de nivel.
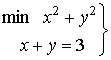
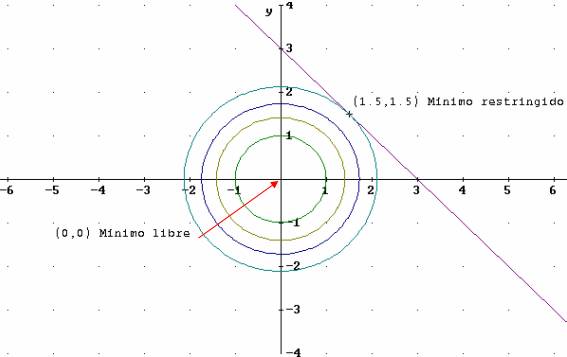 Se trata de determinar el punto de la restricción por el que pasa la curva de nivel más baja.
Se trata de determinar el punto de la restricción por el que pasa la curva de nivel más baja.
ii. Eliminación o sustitución de variables
Ejemplo:
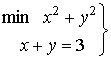 es equivalente a
es equivalente a 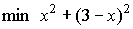
La función objetivo es ahora una función con una variable menos:
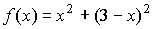
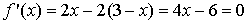
Por tanto, 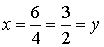
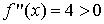
Entonces, 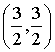 es mínimo restringido o condicionado.
es mínimo restringido o condicionado.
iii. Método de Lagrange
El método consiste en convertir el problema con restricciones de igualdad en uno de óptimos libres, gracias a la incorporación de las restricciones a la función objetivo. Distinguimos dos casos:
En ambos casos, se construye una función, llamada función de Lagrange, y se determina qué puntos cumplen la condición necesaria para ser óptimos del problema y, posteriormente, se estudia si son máximos o mínimos analizando el cumplimiento de la condición suficiente.
Ejemplos de aplicación:
iii.1 Caso de una única restricción
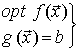 se sustituye por
se sustituye por 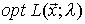
siendo
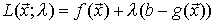 la denominada función de Lagrange que tiene una variable más,
la denominada función de Lagrange que tiene una variable más, 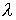 , que recibe el nombre de multiplicador de Lagrange.
, que recibe el nombre de multiplicador de Lagrange.
Observamos que cuando se satisface la restricción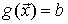 se cumple que
se cumple que 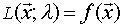
Condición necesaria (Caso m = 1)
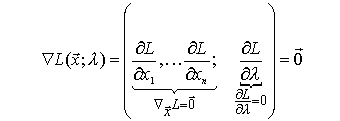
Condición suficiente
Sea un punto 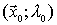 que cumple la condición necesaria; es decir:
que cumple la condición necesaria; es decir:
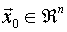 tq
tq 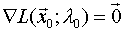
entonces, si denotamos como Hx L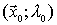 la hessiana de la función de Lagrange en
la hessiana de la función de Lagrange en 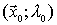 respecto de las variables iniciales (no respecto λ) tenemos:
respecto de las variables iniciales (no respecto λ) tenemos:
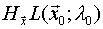 definida positiva
definida positiva 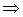
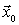 es mínimo condicionado o restringido
es mínimo condicionado o restringido
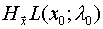 definida negativa
definida negativa 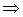
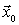 es máximo condicionado o restringido
es máximo condicionado o restringido
en otro caso:
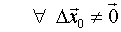 tal que
tal que
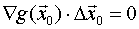
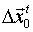
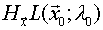
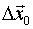 > 0
> 0
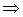
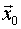 es mínimo condicionado
es mínimo condicionado
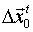
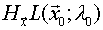
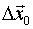 < 0
< 0 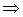
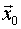 es máximo condicionado
es máximo condicionado
iii.2 Caso de más de una restricción:

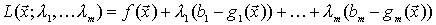
La función L se llama función de Lagrange y los 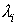 , multiplicadores de Lagrange.
, multiplicadores de Lagrange.
Observamos que se añade un multiplicador 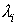 por cada restricción y que cuando se satisfacen todas se cumple que
por cada restricción y que cuando se satisfacen todas se cumple que 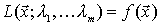
Ejemplo de aplicación 1
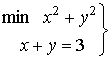
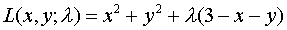
Condición necesaria:
(*)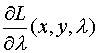 =
= 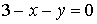
(*)Observemos que la condición 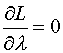 equivale a pedir que se satisfaga la restricción.
equivale a pedir que se satisfaga la restricción.
Resolvemos:
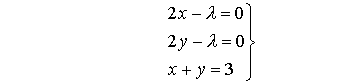
Obtenemos:
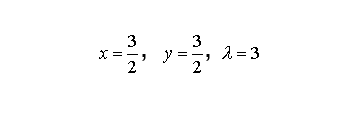
Condición suficiente:
Resultado:
Ejemplo de aplicación 2
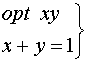
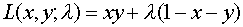
Condición necesaria:
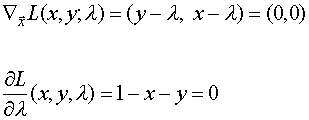
Por lo tanto resolvemos:
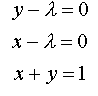
Y obtenemos:
x = ½, y=½ λ=½
Condición suficiente:
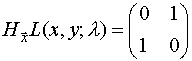 indefinida
indefinida
Veamos qué sucede exactamente sobre la restricción.
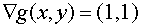
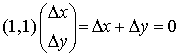
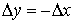
Por tanto, como se comprueba en el gráfico, para mantenernos encima de la restricción es necesario 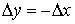
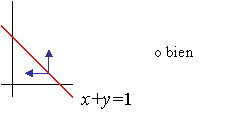 | 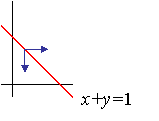 |
Entonces, 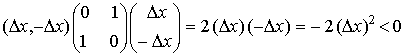
Resultado:
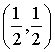
Interpretación de los multiplicadores de Lagrange
Dado un problema con restricciones de igualdad:
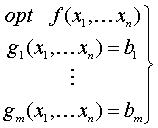
Si se modifica un poco
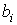 , cambiará también el punto óptimo y, en consecuencia, el valor óptimo.
, cambiará también el punto óptimo y, en consecuencia, el valor óptimo.
Así se entiende que el valor óptimo de un problema es función de cada 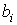 . Pues bien, la derivada de esta función respecto de
. Pues bien, la derivada de esta función respecto de
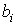 es justamente
es justamente 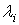
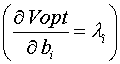 . De aquí se deduce la siguiente fórmula:
. De aquí se deduce la siguiente fórmula:
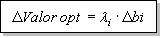
que también se puede escribir como 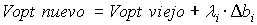
NOTA: Todo esto es cierto para 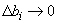 , es decir, cuando se trata de pequeñas variaciones de
, es decir, cuando se trata de pequeñas variaciones de 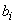 que no afectan al status del problema.
que no afectan al status del problema.

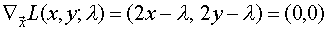
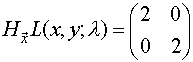
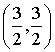 es un
es un