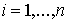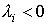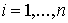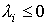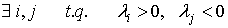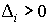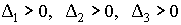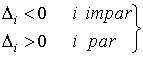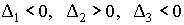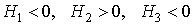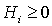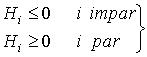Forma Cuadrática
1. Definición de forma cuadrática
Llamamos forma cuadrática a una aplicación Q
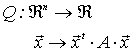
tal que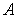 
sea una matriz cuadrada simétrica de orden n.
Una forma cuadrática es un polinomio de 2º grado con n variables:
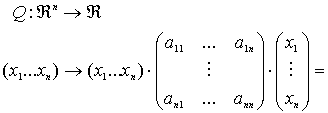
Dado el polinomio es fácil deducir la matriz asociada a la forma cuadrática.
2. Matriz asociada a una forma cuadrática
Resulta muy cómodo, tanto para escribir el polinomio de 2º grado a partir de la matriz, sin tener que hacer la multiplicación:
como para deducir la matriz simétrica asociada a la forma cuadrática a partir del polinomio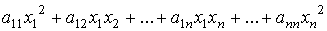 
saber que:
- Los coeficientes de los cuadrados en el polinomio son los elementos de la diagonal de la matriz asociada.
- El elemento
multiplicará a 
y a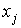 
, es decir, en el polinomio aparecerá: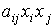 
- El elemento
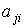multiplicará a 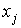y a , es decir, en el polinomio aparecerá: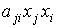 
- Puesto que se trabaja con números reales, se tiene que
(por la propiedad conmutativa) y, por tanto, lo que en realidad aparecerá como consecuencia de los dos apartados anteriores será: 
- Si se desea deducir la matriz simétrica asociada a la forma cuadrática a partir del polinomio, bastará dividir por 2 el coeficiente asociado a cada
y poner el resultado en la fila i, columna 
y en la fila j, columna i
Ejemplos:
Situémonos en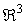 
a) Deducir la forma cuadrática asociada a la matriz
Solución:
Imaginemos la matriz siguiente:
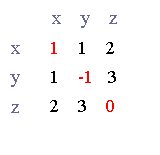
Entonces, la forma cuadrática asociada a esta matriz se expresa como:
b) Deducir la matriz asociada a la siguiente forma cuadrática:
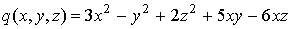
Solución:
,
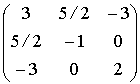
3. Clasificación de una forma cuadrática
Sea 
una forma cuadrática. Se dice que
-
Q es una forma cuadrática definida positiva si
Q es una forma cuadrática definida negativa si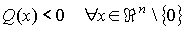
-
Q es una forma cuadrática semidefinida positiva si
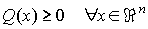
Q es una forma cuadrática semidefinida negativa si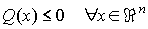
-
Q es una forma cuadrática indefinida si
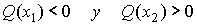
Es fácil clasificar una forma cuadrática cuando sólo aparecen cuadrados en su expresión.
Ejemplo:
Consideremos las siguientes formas cuadráticas:
a)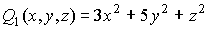 
b) 
c) 
Deducimos cómodamente:
a) 
es
definida positiva
, puesto que en su expresión sólo aparecen cuadrados con coeficientes positivos.
b)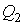 
es
definida negativa
, puesto que en su expresión sólo aparecen cuadrados con coeficientes negativos.
c) 
es
indefinida
, puesto que aunque sólo aparecen cuadrados como en los casos anteriores, los coeficientes son de distinto signo, con lo cual habrá vectores para los que tomará valor positivo y otros para los que tomará valor negativo.
Ejemplo: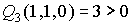 
y 
Cuando no sólo aparecen cuadrados, tenemos que ayudarnos de los distintos métodos de clasificación.
4. Métodos de clasificación de las formas cuadráticas
Se distinguen tres métodos:
i. Por valores propios
Sean 
los valores propios asociados a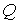 
.
|
1) Q definida positiva (d.p.) |
|
|
1) Q definida negativa (d.n.) |
|
|
2) Q semidefinida positiva (s.d.p.) |
|
|
2) Q semidefinida negativa (s.d.n.) |
|
|
3) Q indefinida |
|
Observación:
Con relación a las formas cuadráticas semidefinidas, nótese que la existencia de un valor propio nulo permite que la imagen por la forma cuadrática de un vector no nulo sea cero.
Ejemplo
Sean los valores propios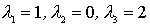 
:
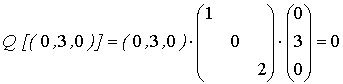
ii. Por menores principales dominantes
Se llama menor principal dominante de A de orden r al determinante de la submatriz formada por las r primeras filas y las r primeras columnas de A.
Escribiremos:
|
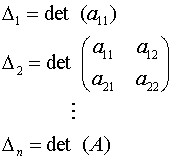
Caso general |
Caso particular n=3 | |
|
1) Q definida positiva |
|
|
|
1) Q definida negativa |
|
|
En cuanto a las formas cuadráticas semidefinidas, los menores principales dominantes sólo proporcionan información en los siguientes casos:
a)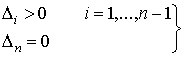 
Q SDP
b)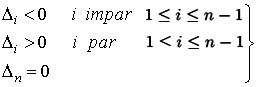 
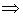Q SDN
(Aquí,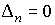 
indica que hay un valor propio igual a cero)
Además, en estos casos, la implicación sólo es cierta en el sentido especificado: no es equivalencia.
iii. Por menores principales
Se llama
menor principal de A de orden r al determinante de cualquier submatriz de dimensión 
tal que su diagonal principal esté formada por elementos de la diagonal principal de A.
Escribiremos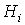 
para designar al conjunto de los menores principales de orden i.
Así, en ℜ3:
Los menores principales proporcionan el siguiente método de clasificación de las formas cuadráticas:
|
Caso general |
Caso particular n=3 | |
|
1) Q definida positiva |
|
|
|
1) Q definida negativa |
|
|
|
|
| |
|
|
| |
|
3) Q indefinida |
Otros casos |
Otros casos |
(La notación 
indica que TODOS los menores principales de orden i deben ser estrictamente positivos. Idénticamente,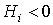 
, 
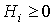, etc.)
Ejemplos de aplicación
Ejemplo 1:
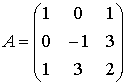
Esta matriz corresponde a una forma cuadrática indefinida, puesto que en la diagonal principal aparecen números positivos y negativos. Observando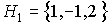 
, vemos que no corresponde ni a 
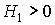, ni a 
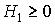, ni tampoco a 
o a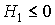 
.
Ejemplo 2:
Esta matriz, atendiendo a los elementos de la diagonal principal, esto es, a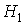 
, podría ser d.p., s.d.p. o indefinida. (Descartamos que corresponda a una forma cuadrática d.n. o s.d.n. puesto que 
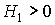y no 
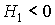, ni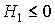 
).
Calculamos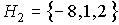 
y observamos un menor de orden 2 negativo, con lo que forzosamente se trata de una forma cuadrática indefinida, puesto que en ningún caso, ni d.p. (o s.d.p.) ni d.n. (o s.d.n.) se tiene 
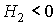. (Compruébese el cuadro).
Ejemplo 3:
Esta matriz, atendiendo a los elementos de la diagonal principal, esto es, a 
, sólo puede ser s.d.p. o indefinida. (
)
Calculamos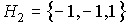 
y observamos dos menores de orden 2 negativos, hecho que nos indica que se trata forzosamente de una forma cuadrática indefinida.
Ejemplo 4:
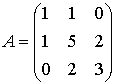
Esta matriz, atendiendo a los elementos de la diagonal principal, esto es, a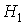 
, sólo puede ser d.p., s.d.p. o indefinida. (
)
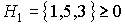Examinamos sus menores principales dominantes:
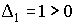
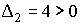
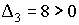
Por tanto, corresponde a una forma cuadrática definida positiva. En este caso, el hecho de analizarlo por menores principales dominantes tiene la ventaja de tener que calcular menos determinantes.