Optimización sin restricciones
1. Formulación del problema:
Sea ƒ: ℜn → ℜ
Un problema de optimización sin restricciones (optimos libres) se formula:
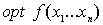
Ejemplo y representación gráfica
|
1) n = 1 |
2) n > 1 |
 |
|
2. Resolución de un problema de optimización.
Condición necesaria. Condición suficiente
Se trata de determinar para qué punto o puntos de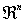 , la función toma el valor máximo o mínimo.
, la función toma el valor máximo o mínimo.
Primeramente es necesario ver qué puntos satisfacen la condición necesaria (C.N.) La idea es poder descartar todos los puntos que NO satisfacen la condición necesaria como posibles óptimos.

Es decir,
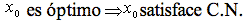
o lo que es equivalente:


Cuando ya hemos determinado el conjunto de puntos que satisfacen la C.N. es necesario ver qué puntos satisfacen la condición suficiente (C.S.), es decir, qué puntos son los verdaderos óptimos.
3. Optimización de una función real de variable real (n=1)
 f continua y derivable en
f continua y derivable en ![]() y
y

Condición necesaria
![]() óptimo local
óptimo local ![]()
Condición suficiente
Sea ![]() un punto que cumple
la condición necesaria
un punto que cumple
la condición necesaria ![]()
![]() mínimo local
mínimo local
![]() máximo local
máximo local
4. Optimización de una función real de más de una variable real (caso general)
ƒ: ℜn → ℜ n ≥1 ƒ con derivadas parciales primeras y segundas continuas y x0 ∈ ℜn
Condición necesaria

Definición: Se llaman puntos críticos o estacionarios aquellos puntos que anulan el gradiente de la función.
Ejemplo:

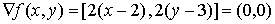
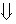

El punto (2,3) satisface la condición necesaria: es un punto crítico.
Habrá que comprobar ahora si cumple la condición suficiente.
Condición suficiente
Se aplica a los puntos  que satisfacen la condición necesaria.
que satisfacen la condición necesaria.
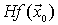 definida positiva
definida positiva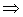
 mínimo local estricto.
mínimo local estricto.
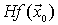 definida negativa
definida negativa 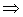
 máximo local estricto.
máximo local estricto.
Ejemplo:
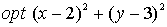
El punto (2,3) satisface la condición necesaria.
Calculamos 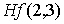
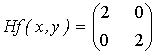


Por tanto,
 corresponde a una forma cuadrática definida positiva, y el punto (2,3) es mínimo local estricto.
corresponde a una forma cuadrática definida positiva, y el punto (2,3) es mínimo local estricto.
Otros casos:
Para  que satisface C.N ( ∇ƒ(
que satisface C.N ( ∇ƒ( )=0 ):
)=0 ):
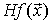 semidefinida positiva
semidefinida positiva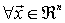
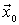 mínimo local y global.
mínimo local y global.
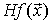 semidefinida negativa
semidefinida negativa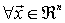
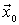 máximo local y global.
máximo local y global.
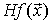 semidefinido positiva
semidefinido positiva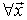 suficientemente cercana a
suficientemente cercana a 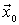
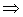
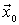 mínimo local.
mínimo local.
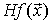 semidefinido negativa
semidefinido negativa 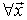 suficientemente cercana a
suficientemente cercana a 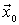
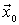 máximo local.
máximo local.
NOTA: Es preciso observar que en estos casos se sustituye la información en un sólo punto que se pedía anteriormente, por información sobre la Hessiana en todo un entorno de 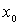 o en todo el dominio, y a cambio se permite debilitar el requerimiento de que sea definida y se consiente en que sea sólo semidefinida.
o en todo el dominio, y a cambio se permite debilitar el requerimiento de que sea definida y se consiente en que sea sólo semidefinida.
