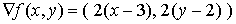Optimización
económica

Grup d'Innovació Docent en Matemàtica Econòmica i Optimització

Optimización con restricciones de desigualdad

1. Formulación del problema

Sean
ƒ: ℜn → ℜ diferenciable
gi:ℜm → ℜi=1..m diferenciables

Un problema diferenciable de optimización con restricciones de desigualdad se formula:

Ejemplo y representación gráfica

  (n=2, m=3)

Nota: Las restricciones de desigualdad definen fronteras al dominio de soluciones factibles .

2. Resolución de un problema de optimización con restricciones de desigualdad

Los siguientes conceptos y teoremas proporcionan los distintos enfoques que conducirán a la resolución del problema.

  1. Aplicación Convexidad. Teorema local-global
  2. Aplicación Curvas de Nivel
  3. Aplicación Teorema de Weierstrass
  4. Aplicación Condiciones de Kuhn-Tucker
  5. Interpretación económica de los multiplicadores de Kuhn-Tucker

i. Aplicación Convexidad. Teorema local-global.

Antes de proceder a la resolución de un problema es importante clasificarlo, estudiando:

a)    La convexidad de la función objetivo.

b)   La continuidad de la función objetivo.

c)    La convexidad del dominio.

d)   La compacidad del dominio.

Ejemplo:

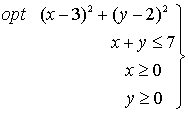
a)    La función objetivo es estrictamente convexa, pues la matriz hessiana de 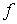 es:

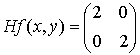
que corresponde a una forma cuadrática definida positiva.

b)    La función objetivo es continua.

c)    El dominio es un conjunto convexo

d)    El dominio es un conjunto compacto

Por tanto:

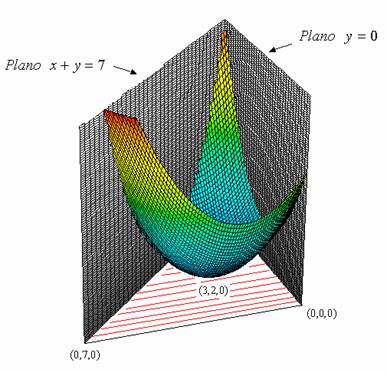
ii. Aplicación Curvas de Nivel.

Ejemplo:

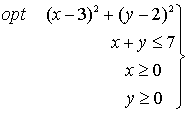
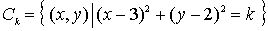
Observemos que la ecuación 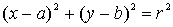 corresponde a una circunferencia centrada en (a,b) de radio .

Por tanto, se tratará de circunferencias concéntricas centradas en el punto (3,2).

Del dibujo de las curvas de nivel podemos deducir:

·        (3,2) es mínimo global. 

·        (0,7) es máximo global.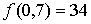  

·        (0,0) es máximo local.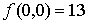 

·        (7,0) es máximo local.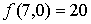 

También se deduce que:

·        (0,2) no es óptimo local. 

Notar que por la zona del dominio pintada en azul pasan curvas de niveles más bajos que las que pasan por el punto (0,2) y que por la zona del dominio pintada en amarillo pasan curvas de niveles más altos.

Por tanto, por el entorno del punto (0,2) que está dentro del dominio (representado por el semicírculo en línea continua) pasan curvas de niveles más altos y más bajos,por lo que no puede ser ni máximo ni mínimo local.

Ejercicio:

El lector puede repetir el razonamiento anterior para los puntos (4,3) y (3,0):

·        (4,3) no es óptimo local.

·        (3,0) no es óptimo local.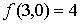

iii. Aplicación Teorema de Weierstrass.

Ejemplo:

Puesto que la función objetiv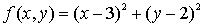o  es una función continua y el dominio 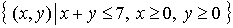 es un conjunto compacto:
 

podemos aplicar el teorema de Weirstrass y deducir que el problema tiene máximo global y mínimo global.

Para deducir cuáles son los óptimos, basta construir el conjunto formado por:

  1. Los puntos que cumplen la condición necesaria de óptimos libres ().
  2. Los puntos que cumplen la condición necesaria de óptimos restringidos sobre cada una de las restricciones que definen el dominio tomadas como restricciones de igualdad. Es decir, que satisfacen la condición necesaria de óptimo restringido sobre cada una de las fronteras del dominio ().
  3. Los vértices del dominio ().

Una vez reunidos todos estos puntos, bastará calcular su imagen. El que tenga la imagen mayor será el máximo global y el que la tenga menor, el mínimo global.

Ejemplo:

1.     Calculamos el gradiente de la función objetivo y lo igualamos a cero.

 = (0,0)
Por tanto: 
Resultado: 

2.    Calculamos los puntos que cumplen la condición necesaria de óptimos restringidos sobre cada una de las restricciones que definen el dominio tomadas como restricciones de igualdad

Cuadro de texto: Sustituyendo en la función a optimizar queda: que equivale a: Derivando e igualando a cero: Sustituyendo el resultado en la restricción obtenemos: Por tanto, el punto hallado es el (4,3)

Cuadro de texto: Sustituyendo en la función a optimizar queda: que equivale a: Derivando e igualando a cero: Por tanto, el punto hallado es el (0,2)

Cuadro de texto: Sustituyendo en la función a optimizar queda: que equivale a: Derivando e igualando a cero: Por tanto, el punto hallado es el (3,0)

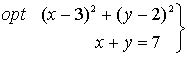
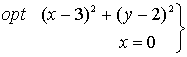
Resultado: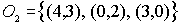 

3.     El conjunto de vértices es

Entonces el conjunto de todos los puntos candidatos a óptimo es:

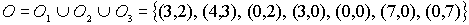
Calculamos ahora sus imágenes:

Por tanto:

·        (3,2) es el mínimo global y el valor mínimo es 0.

·        (0,7) es el máximo global y el valor máximo es 34.

iv. Aplicación Condiciones de Kuhn-Tucker.

En los casos en que no sea factible el método gráfico, habrá que resolver el problema analíticamente aplicando las condiciones de Kuhn-Tucker.

Nota: No obstante, la fuerza del método gráfico de las curvas de nivel no la tienen las condiciones de K-T.

Ejemplo:

En

El punto (4,3) satisface K-T para máximo, ya que los multiplicadores son todos mayores o iguales a cero, de lo que se deduce(*) que es un posible máximo. Sin embargo, las curvas de nivel ponen de manifiesto que (4,3) NO es óptimo local.

(*)  Las condiciones de K-T son sólo necesarias en este ejemplo porque la función objetivo no es cóncava.

v. Interpretación económica de los multiplicadores de Kuhn-Tucker.

Ejemplo:

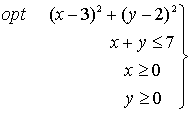
Supongamos que la función objetivo es una función de producción. Podríamos preguntarnos: ¿Se conseguiría mejorar la producción si la restricción 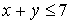 pasase a ser ?

Se observa que el incremento en el valor del término independiente de una restricción con signo  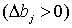, representa incrementar el dominio y, por tanto, ofrece la posibilidad de hallar nuevos puntos que mejoren los óptimos ya obtenidos: podríamos encontrar un máximo “más alto” o un mínimo “más bajo”.

Ejemplo:

En nuestro ejemplo, el mínimo permanece igual, pero el máximo sí mejora.

La fórmula coincide con la ya obtenida para la interpretación de los multiplicadores de Lagrange en problemas con restricciones de igualdad:

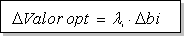
Cuadro de texto:

Podemos comprobar que esta fórmula concuerda con lo que acabamos de explicar, puesto que si se trata de máximos, los multiplicadores serán positivos o nulos y obtendremos:

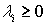    (pues  y )
es decir, el valor máximo será mayor

En cambio, en el caso de mínimos, los multiplicadores serán negativos o nulos y obtendremos:

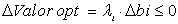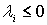    (pues  y )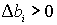
es decir, el valor mínimo será menor

Ejemplo:

Repetimos en nuestro ejemplo el razonamiento para el caso en que nos propusiéramos pasar de 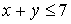 a  .

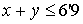Un decremento en el valor del término independiente de una restricción con signo 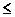 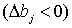 representa disminuir el dominio y sólo ofrece la oportunidad de “perder” óptimos y, por tanto, podríamos encontrarnos máximos “más bajos” y mínimos “más altos”.

Condiciónes de Kuhn-Tucker(K-T)

Sea (P) un problema con restricciones de desigualdad:


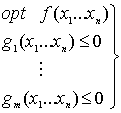
(f, gi funciones diferenciables)

  1. Condiciones necesarias de primer orden de optimalidad local
  2. Enunciado de las condiciones
  3. Deducción geométrica
  4. Suficiencia y convexidad

Ver ejemplo de aplicación

i. Condiciones necesarias de primer orden de optimalidad local

Las condiciones de K-T son necesarias de optimalidad local, es decir:

máximo local   satisface K-T para máximo
mínimo local   satisface K-T para mínimo

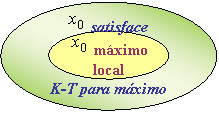
Los dibujos aclaran el hecho de que estas implicaciones sean iguales a:

 NO satisface K-T para máximo  NO es máximo local
 NO satisface K-T para mínimo  NO es mínimo local

En definitiva, si un punto satisface las condiciones de K-T para máximo, sólo podemos decir que es un “posible” máximo local; si en cambio, no las satisface, sí podremos asegurar que NO es máximo local.

ii. Enunciado de las condiciones

Las condiciones de K-T son:

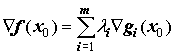
  1. (Los 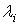reciben el nombre de multiplicadores de K-T)

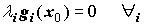
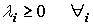  3. (si se trata de máximo)

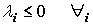     (si se trata de mínimo)

Geométricamente, indican que en un punto de posible máximo, el gradiente de la función objetivo es combinación lineal positiva de los gradientes de las restricciones saturadas en . De igual forma, indican que en un punto de posible mínimo, el gradiente de la función objetivo es combinación lineal negativa de los gradientes de las restricciones que se saturan en .

Nomenclatura:

Diremos que un punto satisface K-T para máximo cuando satisface las condiciones de K-T con

Diremos que un punto satisface K-T para mínimo cuando satisface las condiciones de K-T con

Explicación:

Condición 1: Obliga a que el gradiente de la función objetivo en x0 sea combinación lineal de los gradientes de las restricciones en x0 .

Condición 2: Obliga a que los multiplicadores de K-T asociados a restricciones NO saturadas en x0  sean nulos. Veámoslo:

  1. Si la restricción gi  está saturada en x0: ( gi(x0) = 0)  entonces: λi gi(x0) = 0 para cualquier valor de λi
  2. Si la restricción gi  NO está saturada en x0: ( gi(x0) < 0)  entonces la única posibilidad para que λi gi(x0) = 0  es que λi = 0

Condición 3: Cuando el punto satisface K-T para máximo, todos los multiplicadores deben ser positivos. Cuando el punto satisface K-T para mínimo, todos los multiplicadores deben ser negativos.

Condición 4: El punto x0  debe satisfacer todas las restricciones del problema, es decir, debe pertenecer al conjunto de soluciones factibles del problema.

iii. Deducción geométrica

Sea el problema:

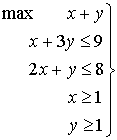
Debemos considerar todas las restricciones en el sentido 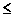; para ello multiplicaremos las que estén en sentido contrario por  –1. Es decir:

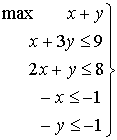
La función objetivo es 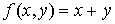 cuyo gradiente es: .

Dibujemos el dominio del problema y las curvas de nivel de la función objetivo:

Fácilmente se comprueba que (1,1) es mínimo local y (3,2) es máximo global .

Las restricciones son:

Dibujando en cada vértice el gradiente de las restricciones que se saturan en él y el de la función objetivo obtenemos:

Se observa que únicamente en el máximo, el gradiente de la función objetivo queda dentro del cono convexo generado por los gradientes de las restricciones saturadas; es decir, únicamente en el máximo, el gradiente de la función objetivo se puede obtener como combinación lineal positiva de los gradientes de las restricciones saturadas.

Se aprecia también que en el mínimo, el gradiente de la función objetivo se obtiene como combinación lineal negativa de los gradientes de las restricciones saturadas.

iv. Suficiencia y convexidad

Las condiciones de K-T, que son sólo necesarias en general, son también suficientes cuando hay convexidad: 

1.     ƒ:D ⊂ ℜn → ℜ        D conjunto convexo,  ƒ convexa

x0 satisface K-T para mínimo ⇔ x0  es mínimo local

2.     ƒ:D ⊂ ℜn → ℜ        D conjunto convexo, ƒ cóncava

x0 satisface K-T para máximo ⇔ x0  es máximo local

Observación:

Notemos que teniendo en cuenta el teorema local-global, aún podremos decir más:

1.     ƒ:D ⊂ ℜn → ℜ        D conjunto convexo,  ƒ convexa

x0 satisface K-T para mínimo ⇔ x0 mínimo local ⇔ x0 mínimo global

2.     ƒ:D ⊂ ℜn → ℜ        D  conjunto convexo, ƒ cóncava

x0 satisface K-T para máximo ⇔ x0 máximo local ⇔ x0 máximo global

Ejemplo de Aplicación

Sea el problema:

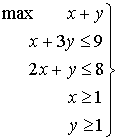
Muy importante: debemos considerar todas las restricciones en el sentido ; para ello multiplicaremos las que estén en sentido contrario por  –1. Es decir:

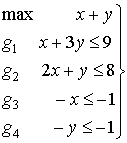
Apliquemos las condiciones de K-T al punto (3,2):

A)   Tras comprobar que el punto es del dominio del problema ( condición 4), proseguimos con la condición 2: las restricciones que se saturan en (3,2) son  y 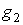; por tanto, los multiplicadores asociados a las restantes restricciones serán nulos, es decir

B)   Planteamos la condición 1, prescindiendo de las restricciones no saturadas:

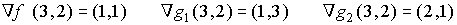
Por tanto: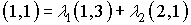

De donde se deduce que: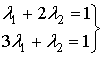

C)  Comprobamos el signo de los multiplicadores (condición 3).

En este caso, 

D)  Deducimos las consecuencias: puesto que se trata de un problema lineal, la función objetivo es cóncava y convexa y el dominio es convexo. Por tanto, las condiciones de K-T son necesarias y suficientes tanto para mínimo como para máximo.

Así pues, si el punto (3,2) satisface K-T para máximo, podemos asegurar que (3,2) es máximo local y por el teorema local-global, también es máximo global.