Conocimientos Iniciales
Bola
Definición:
Se llama bola abierta de centro x0 y radio r y se escribe  al conjunto de puntos
al conjunto de puntos 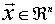 tales que su distancia a x0 es menor que r.
tales que su distancia a x0 es menor que r.

A veces se habla también de “entorno de x0” correspondiendo al mismo concepto.
Nota: Las bolas en ℜ son los intervalos.
Combinación lineal negativa
Definición:
Sean 
Se llama combinación lineal negativa de los
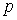 puntos
puntos
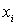 a:
a:
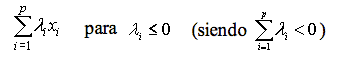
Ejemplo:
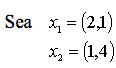
Las combinaciones lineales negativas se obtendrán sustituyendo 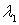 y
y 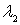 por valores reales negativos (se pide que no sean nulos los dos a la vez):
por valores reales negativos (se pide que no sean nulos los dos a la vez):
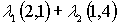
Obsérvese que al variar 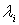 de esta manera obtenemos:
de esta manera obtenemos:
Combinación lineal positiva
Definición:
Sean 
Se llama combinación lineal positiva de los 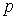 puntos
puntos 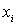 a:
a:
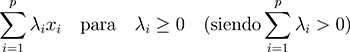
Ejemplo:
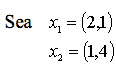
Las combinaciones lineales positivas se obtendrán sustituyendo 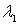 y
y 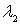 por valores reales positivos (se pide que no sean nulos los dos a la vez):
por valores reales positivos (se pide que no sean nulos los dos a la vez):
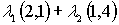
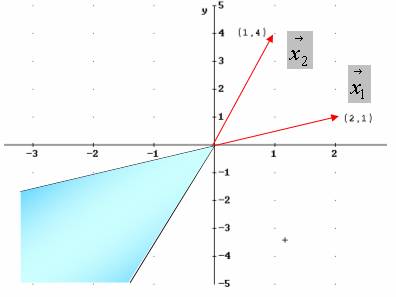
Obsérvese que al variar 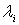 de esta manera obtenemos justamente el cono convexo generado por los vectores
de esta manera obtenemos justamente el cono convexo generado por los vectores 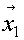 y
y 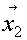
Conjunto abierto
Definición:
Sea 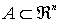
 abierto
abierto 
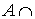 Fr A
Fr A 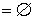
Intuitivamente:
Un conjunto es abierto si y sólo si no contiene ningún punto frontera.
Ejemplo:
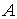 =
=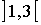
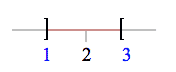
Observemos que 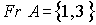 , es decir, el conjunto de puntos frontera de
, es decir, el conjunto de puntos frontera de 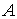 sólo contiene dos puntos:
sólo contiene dos puntos: 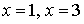 y estos puntos NO pertenecen a
y estos puntos NO pertenecen a 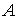 puesto que se ha considerado el intervalo abierto.
puesto que se ha considerado el intervalo abierto.
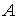 =
=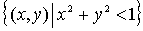
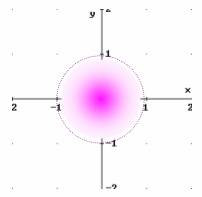
Observemos que 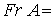
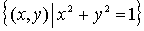 , es decir, la frontera es justamente la circunferencia que NO pertenece al conjunto.
, es decir, la frontera es justamente la circunferencia que NO pertenece al conjunto.
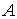 =
=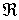
Observemos que 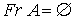 , es decir, ningún punto es punto frontera y, por tanto,
, es decir, ningún punto es punto frontera y, por tanto, 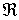 es abierto.
es abierto.
Igualmente, 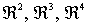 y en general
y en general 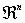 son conjuntos abiertos.
son conjuntos abiertos.
NOTA: Obsérvese que todos los conjuntos que aparecen en el ejemplo 3 son también conjuntos cerrados.
Conjunto acotado
Definición:
Sea 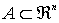
Se dice que 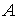 es acotado si dado un punto
es acotado si dado un punto 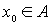 existe un radio finito
existe un radio finito 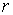 tal que
tal que 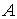 queda incluido en una bola centrada en
queda incluido en una bola centrada en 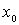 y radio
y radio 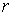 , es decir:
, es decir:
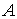 acotado
acotado 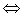
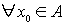
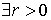 tq
tq 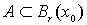
Ejemplos de conjuntos acotados:
-
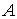 =
=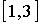
-
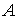 =
=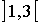
-
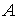 =
=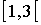
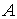 =
=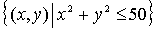
Ejemplos de conjuntos NO acotados:
-
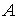 =
=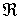
-
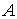 =
=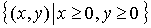
-
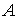 =
=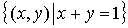
-
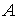 =
=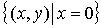
Observemos que en estos últimos cuatro ejemplos no hay manera de incluir el conjunto en una bola por grande que sea el radio.
Conjunto cerrado
Definición:
Sea 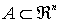
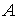 cerrado
cerrado 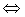 Fr A
Fr A 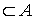
Intuitivamente:
Un conjunto es cerrado si y sólo si contiene todos los puntos de su frontera.
Ejemplo:
-
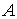 =
=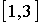
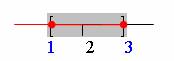
Observemos que
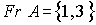 , es decir, el conjunto de puntos frontera de
, es decir, el conjunto de puntos frontera de 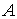 sólo contiene dos puntos:
sólo contiene dos puntos: 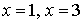 y estos puntos pertenecen a
y estos puntos pertenecen a 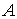 puesto que se ha considerado el intervalo cerrado.
puesto que se ha considerado el intervalo cerrado. -
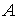 =
=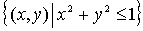
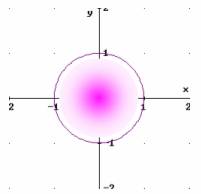
Observemos que
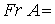
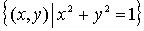 , es decir, la frontera es la circunferencia que pertenece al conjunto.
, es decir, la frontera es la circunferencia que pertenece al conjunto.
-
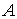 =
=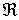
Observemos que
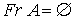 , es decir, ningún punto es punto frontera y debido a que, por convenio, el conjunto vacío está incluido en cualquier conjunto (
, es decir, ningún punto es punto frontera y debido a que, por convenio, el conjunto vacío está incluido en cualquier conjunto (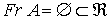 ), se puede considerar
), se puede considerar 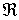 como conjunto cerrado.
como conjunto cerrado.Igualmente,
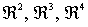 y en general
y en general 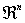 son conjuntos cerrados.
son conjuntos cerrados.
NOTA: Obsérvese que todos los conjuntos que aparecen el ejemplo 3 son también conjuntos abiertos.
Conjunto compacto
Definición:
Sea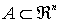
Ejemplo:
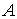 =
=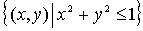
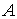 =
=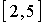
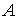 =
=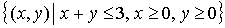
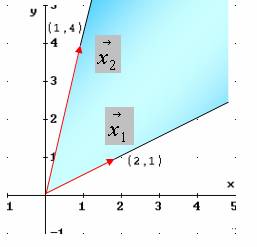
Conjunto convexo de ℜn
Definición:
C 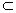 ℜn
ℜn
C convexo ⇔ ∀ x1, x2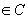
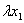 +
+ 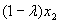
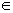 C
C 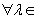 [0,1]
[0,1]
Intuitivamente:
Decimos que C es un conjunto convexo si cualquier segmento que una dos puntos cualesquiera del conjunto, siempre pertenece , todo él, al conjunto.
Ejemplos:
-
Conjuntos convexos:

-
Conjuntos no convexos:
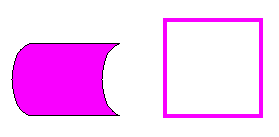
- Los intervalos son los conjuntos convexos de ℜ.
Propiedades:
 C1
C1
 C2 convexo
C2 convexo
 C1 + C2 convexo
C1 + C2 convexo
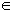 R
R
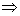 kC convexo
kC convexo
Conjunto de soluciones factibles o dominio del problema
Definición:
Es el conjunto de los puntos que satisfacen todas las restricciones de un problema. Es dentro de ese conjunto donde deberán buscarse los óptimos.
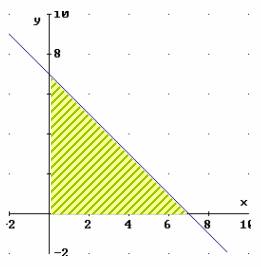
Ejemplo
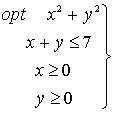
El conjunto de soluciones factibles o dominio del problema es:
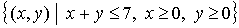
Óptimo / Extremo
Óptimo y extremo son términos que designan tanto mínimo como máximo.
Cono en ℜn
Definición:
S es un cono 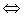
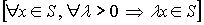
Ejemplos:

Nota: Nótese que si sacáramos el origen del conjunto, éste seguiría siendo cono.
Cono convexo generado por un conjunto
Definición:
Se denomina cono convexo generado por un conjunto  y se escribe conv cone S al cono convexo más pequeño que contiene S.
y se escribe conv cone S al cono convexo más pequeño que contiene S.
Ejemplo 1:
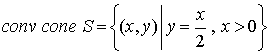
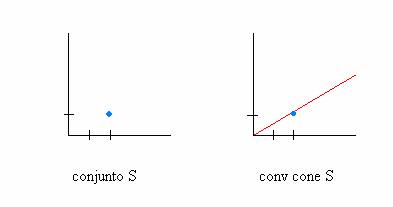
Ejemplo 2:
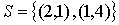
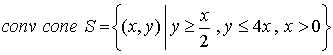
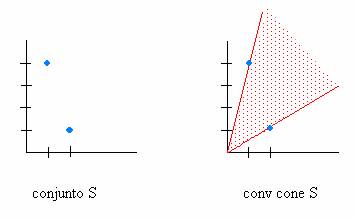
Convexidad. Programa convexo. Programa cóncavo
Considérense los siguientes problemas:
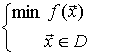 cuando la gráfica de f es
cuando la gráfica de f es

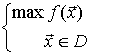 cuando la gráfica de f es
cuando la gráfica de f es
En ambos casos, el problema de optimización se reduce a calcular el punto en el que la derivada se anula:

y se obtiene en el primer caso un mínimo global o absoluto, y en el segundo caso un máximo global o absoluto.
Esto explica la gran importancia del concepto de convexidad en optimización.
Un problema del tipo
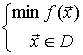 donde f es una función convexa y D un dominio convexo
donde f es una función convexa y D un dominio convexo
se llama problema convexo o programa convexo.
Paralelamente,
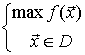 donde f es una función cóncava y D un dominio convexo
donde f es una función cóncava y D un dominio convexo
se llama problema cóncavo o programa cóncavo o problema convexo para maximizar.
NOTA: Obsérvese que una función convexa no ofrece, en cambio, ninguna ventaja si lo que se quiere conseguir es un máximo; ni una función cóncava, si lo que se quiere conseguir es un mínimo.
Curva de nivel
Definición:
Sea ƒ: D⊂ℜn→ℜ y k∈ℜ
La curva de nivel k de la función ƒ está formada por todos los puntos del dominio D cuya imagen es k.
Es decir:
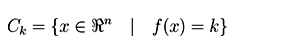
Ejemplo 1:
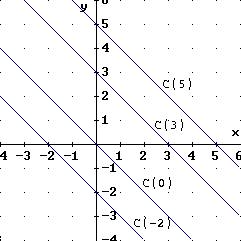
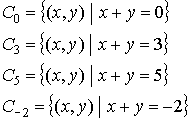
En cambio, la representación de las curvas de nivel se hace sobre el dominio, que es en ℜ2, uniendo todos los puntos que tienen la misma imagen.
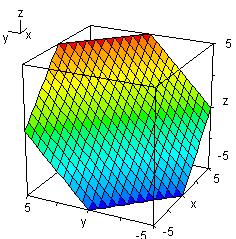
Ejemplo 2:
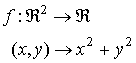
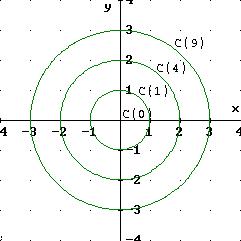
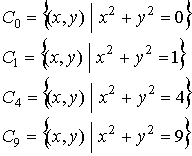
-
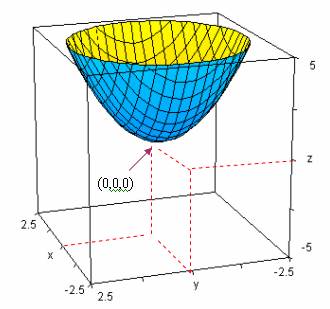
La ecuación
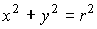 corresponde a una circunferencia centrada en el origen con radio
corresponde a una circunferencia centrada en el origen con radio 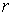 . Por tanto, las curvas de nivel de esta función son circunferencias concéntricas y no hay curvas de niveles negativos.
. Por tanto, las curvas de nivel de esta función son circunferencias concéntricas y no hay curvas de niveles negativos.
-
La gráfica de la función en ℜ3 es:
Dominio de la función
Definición:
Es el conjunto de puntos para los que está definida una función.
Ejemplo:
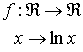
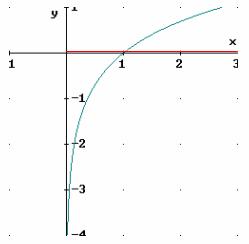
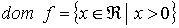 (en el gráfico está en línea roja)
(en el gráfico está en línea roja)
El dominio de la función está formado por los números reales estrictamente positivos porque no existe el logaritmo neperiano de números negativos ni el logaritmo neperiano de cero.
Ecuación de una circunferencia
La ecuación de una circunferencia de radio r y de centro en 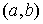 es:
es:
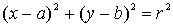
Cuando está centrada en el origen 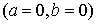 se tiene:
se tiene:
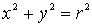
Envolvente convexa
Definición:
Sea 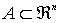
La envolvente convexa de A (conv A) es el conjunto convexo más pequeño que contiene a A.
Ejemplo:

Propiedades:
A convexo 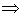 A = conv A
A = conv A
Frontera de un conjunto
Definición:
Sea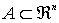 y
y 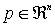
Se dice que p es un punto frontera de A si y sólo si cualquier bola centrada en p, tiene intersección no vacía tanto con A como con el complementario de A (ℜn \ A)
Es decir,
Sea 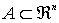 y
y 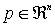
p es un punto frontera de A 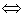
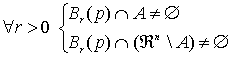
Ejemplo:
Sea A:
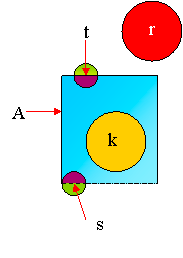
-
k 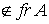 puesto que hemos hallado una bola cuya intersección con el complementario de
A es vacía.
puesto que hemos hallado una bola cuya intersección con el complementario de
A es vacía.
-
r 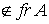 puesto que hemos hallado una bola cuya intersección con
A es vacía.
puesto que hemos hallado una bola cuya intersección con
A es vacía.
-
t y
s 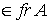 puesto que tanto si hacemos la bola más grande como si la hacemos más pequeña, ésta sigue teniendo una intersección no vacía con
A (color lila) y con el complementario de
A (color verde).
puesto que tanto si hacemos la bola más grande como si la hacemos más pequeña, ésta sigue teniendo una intersección no vacía con
A (color lila) y con el complementario de
A (color verde).
Nota: Observamos que s no pertenece a A, aunque sí que pertenece, como se ha explicado, a la frontera de A.
Función cóncava. Función estrictamente cóncava
Definición intuitiva:
Una función es cóncava si y sólo si al unir dos puntos cualesquiera de la gráfica de la función, el segmento que los une queda por debajo (o coincide) con la gráfica.
Ejemplos:
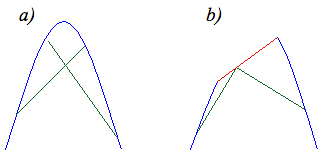
En el ejemplo a) la función se llama estrictamente cóncava porque el segmento queda siempre estrictamente por debajo de la gráfica.
En el ejemplo b) la función es cóncava pero no estrictamente, porque si se toman dos puntos sobre la zona roja de la gráfica, el segmento coincide con ella.
Definición:
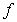 cóncava
cóncava 
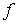 estrictamente cóncava
estrictamente cóncava 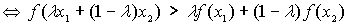
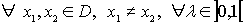
Caracterización:
ƒ cóncava ⇔ Hƒ(x) semidefinida negativa 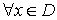
ƒ estrictamente cóncava ⇐ Hƒ(x) definida negativa 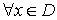
ƒ estrictamente cóncava ⇒ Hƒ(x) semidefinida negativa 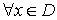
Ejemplos:
1.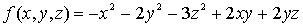
Consideramos su matriz hessiana: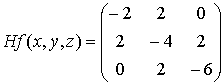
Observamos que es definida negativa 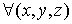 .
.
Por tanto, deducimos que 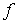 es estrictamente cóncava.
es estrictamente cóncava.
Propiedades:
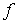 convexa
convexa 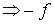 cóncava
cóncava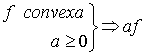 convexa
convexa- Una función lineal es cóncava y convexa simultáneamente.
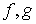 convexas
convexas 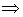
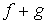 convexa
convexa
Función convexa. Función estrictamente convexa
Definición intuitiva:
Una función es convexa si y sólo si al unir dos puntos cualesquiera de la gráfica de la función, el segmento que los une queda por encima (o coincide) con la gráfica.
Ejemplos:
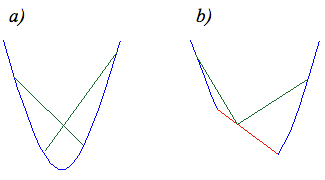
En el ejemplo a) la función se llama estrictamente convexa porque el segmento queda siempre estrictamente por encima de la gráfica.
En el ejemplo b) la función es convexa pero no estrictamente, porque si se toman dos puntos sobre la zona roja de la gráfica, el segmento coincide con ella.
Definición:
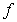 convexa
convexa 
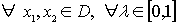
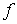 estrictamente convexa
estrictamente convexa 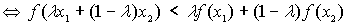
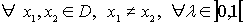
Caracterización:
ƒ convexa ⇔ Hƒ(x) semidefinida positiva 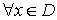
ƒ estrictamente convexa ⇐ Hƒ(x) definida positiva 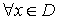
ƒ estrictamente convexa ⇒ Hƒ(x) semidefinida positiva 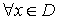
Ejemplos:
-
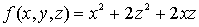
Consideramos su matriz hessiana:
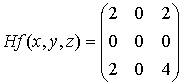
Observamos que es semidefinida positiva
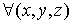 .
.Por tanto, deducimos que
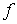 es convexa.
es convexa. -
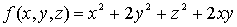
Consideramos su matriz hessiana:
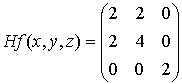
Observamos que es definida positiva
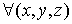 .
.Por tanto, deducimos que
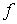 es estrictamente convexa.
es estrictamente convexa.
Propiedades:
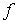 convexa
convexa 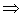
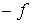 cóncava
cóncava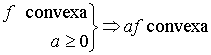
- Una función lineal es cóncava y convexa simultáneamente.
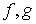 convexas
convexas 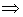
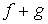 convexa
convexa
Función creciente
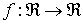
Definición: f es creciente en 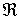
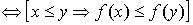
Gráfica de funciones crecientes:
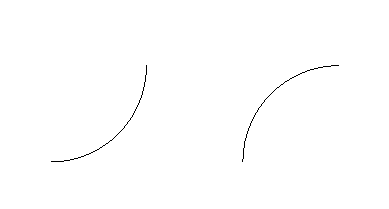
Propiedad:
Las pendientes de las rectas tangentes a la gráfica de una función creciente son siempre positivas.
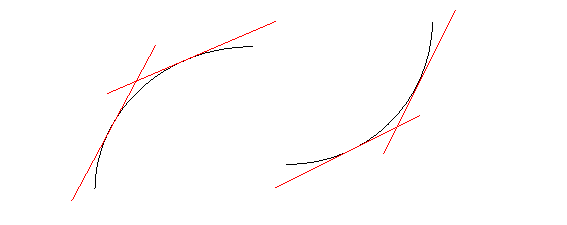
En otras palabras, la derivada de una función creciente es positiva.
Más aún:
Proposición: f creciente en 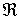
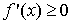
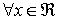
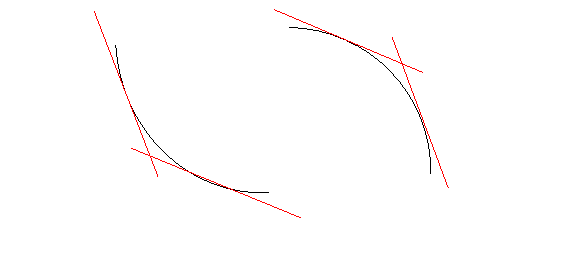
Función decreciente
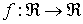
Definición: f es decreciente en 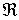
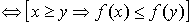
Gráfica de funciones decrecientes:

Propiedad:
Las pendientes de las rectas tangentes a la gráfica de una función decreciente son siempre negativas.
En otras palabras, la derivada de una función decreciente es negativa.
Más aún:
Proposición: f decreciente en 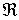
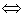
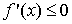
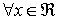
Función diferenciable
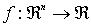
ƒ diferenciable en 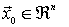 ⇔ existe en
⇔ existe en 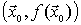 un único hiperplano tangente que aproxima el valor de la función alrededor de este punto.
un único hiperplano tangente que aproxima el valor de la función alrededor de este punto.
Ver caso n = 1
Proposición:
f tiene derivadas parciales continuas en 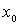 ⇒ f diferenciable en
⇒ f diferenciable en 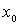 ⇒ f continua en
⇒ f continua en 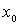 .
.
Ejemplo:
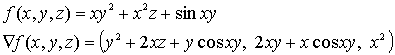
Se obtienen las siguientes funciones como derivadas parciales:
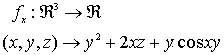
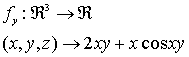
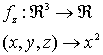
y puesto que 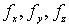 son continuas en
son continuas en 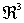 , podemos asegurar que la función f es diferenciable en
, podemos asegurar que la función f es diferenciable en 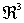 .
.
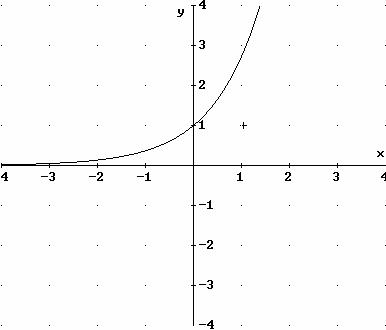
Función exponencial
La función exponencial es una función real de variable real definida como

donde a se llama base de la función exponencial.
Frecuentemente, la base de la función exponencial es el número irracional e cuyo valor es e = 2,718282…
Entonces, la representación gráfica de la función 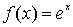 es:
es:
Función lineal
Definición:
Es una función del tipo
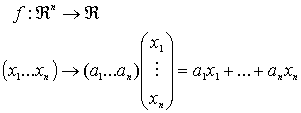
Una función lineal es un polinomio de 1º grado con n variables.
Propiedad:
Función objetivo
Definición:
Es la función que se pretende minimizar o maximizar en un programa matemático.
Ejemplo:
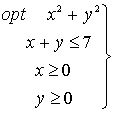
La función objetivo es 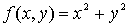
Gradiente de una función
Sea ƒ: ℜn→ℜ
Se llama gradiente de ƒ y se escribe ∇ƒ al vector formado por las derivadas parciales de ƒ
Ejemplo:
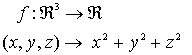
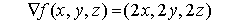
El vector gradiente calculado en un punto es un vector numérico.
Ejemplo:
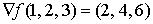
Hessiana de una función
Definición:
Sea ƒ: ℜn→ℜ
Se llama matriz hessiana de ƒ y se escribe Hƒ a la matriz formada por las derivadas parciales segundas de ƒ
Por ejemplo, para ƒ: ℜ3→ℜ
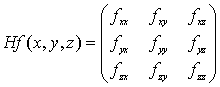
donde ƒxz indica la derivada respecto de z de la derivada parcial respecto de x
La matriz hessiana de ƒ calculada en un punto es una matriz numérica.
La matriz hessiana de ƒ resulta ser una matriz simétrica (Teorema de Schwarz)
Ejemplo:
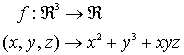
Calculemos las derivadas parciales primeras que forman el gradiente de ƒ

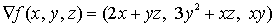
Calculemos la matriz hessiana
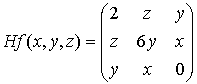
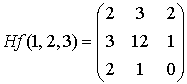
Hiperplano en ℜn
Definición:
Sea a ∈ ℜn, k ∈ ℜ
Un conjunto H tal que H=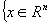
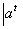 x= k
x= k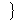 se llama hiperplano.
se llama hiperplano.
Ejemplos:
-
Si n=2 y a =(1,3) y k=5
H =
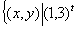 (x,y) = 5
(x,y) = 5
H es una recta : x +3y =5
-
Si n=3 y a =(2, -1, 3) y k=12
H =
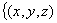
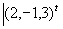 (x,y,z) = 12
(x,y,z) = 12
H es un plano: 2x – y + 3z = 12
Si n>3, H es un hiperplano.
Propiedad:
Un hiperplano es un conjunto convexo.
Teorema local-global o teorema fundamental de la programación convexa
A)
Sea ƒ: D⊂ℜn → ℜ siendo D un conjunto convexo no vacío y ƒ una función convexa.
Entonces,
a) Si 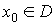 es mínimo
local de
es mínimo
local de 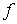 en
en 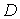 , también es mínimo global.
, también es mínimo global.
b) El conjunto de mínimos locales de 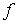 en
en 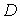 es un conjunto
convexo.
es un conjunto
convexo.
Nota: Este teorema se puede “entender” fácilmente razonando sobre la gráfica de una función convexa.
B)
Sea 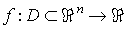 siendo
siendo 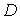 un conjunto convexo no vacío y
un conjunto convexo no vacío y 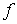 una función cóncava.
una función cóncava.
Entonces,
a) Si 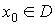 es máximo
local de
es máximo
local de 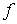 en
en 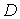 , también es máximo global.
, también es máximo global.
b) El conjunto de máximos locales de 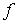 en
en 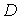 es un conjunto convexo.
es un conjunto convexo.
Máximo local, mínimo local, máximo global, mínimo global
Sea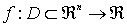 y sea
y sea 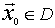
Consideramos que D es la intersección entre el dominio de la función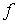 y el conjunto de soluciones factibles.
y el conjunto de soluciones factibles.
Definiciones:
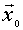 es un máximo global
o absoluto de
es un máximo global
o absoluto de 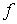 en D
en D
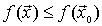
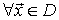
(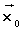 es un máximo global o absoluto de
es un máximo global o absoluto de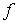 en D si su imagen es mayor o igual que la de cualquier otro punto del dominio)
en D si su imagen es mayor o igual que la de cualquier otro punto del dominio)
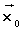 es un mínimo global o
absoluto de
es un mínimo global o
absoluto de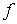 en D
en D 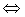
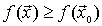
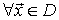
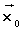 es un máximo local o relativo de
es un máximo local o relativo de 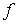 en D
en D 
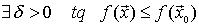
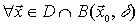
(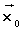 es un máximo local o relativo de
es un máximo local o relativo de 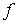 en D si existe una bola centrada en
en D si existe una bola centrada en 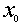 , un entorno de
, un entorno de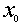 , donde la imagen de
, donde la imagen de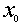 sea mayor o igual que la de los otros puntos)
sea mayor o igual que la de los otros puntos)
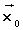 es un mínimo local o relativo de
es un mínimo local o relativo de 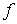 en D
en D 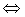
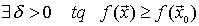
Cuando las desigualdades se satisfacen de forma estricta, se dice que los óptimos son estrictos.
Gráficamente (caso n = 1):
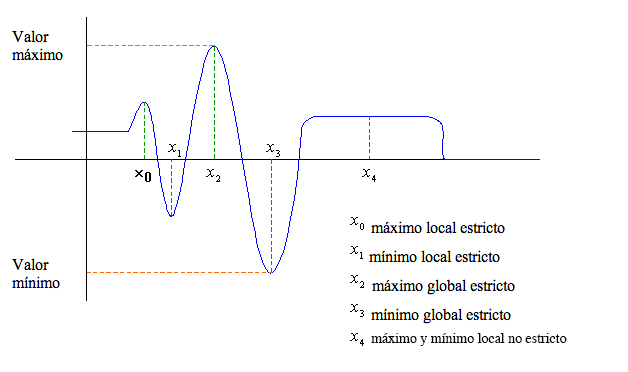
Propiedades:
1. Todo máximo/mínimo global es local.
2. Todo máximo/mínimo global estricto es único.
Genéricamente se denomina extremo relativo a un máximo o mínimo local
Punto de inflexión
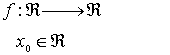 ƒ dos veces derivable
ƒ dos veces derivable
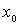 es punto
de inflexión de ƒ ⇔ la función
cambia el sentido de la curvatura en
es punto
de inflexión de ƒ ⇔ la función
cambia el sentido de la curvatura en ![]() .
.
Es decir, los puntos de inflexión son aquellos en los que la función pasa de cóncava a convexa o viceversa. En ellos, la tangente a la gráfica, corta la gráfica.
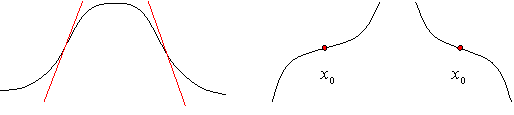
Proposición:
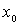 es punto de
inflexión ⇒
es punto de
inflexión ⇒ 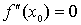
Punto de silla
Definición:
Sea 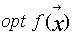 un problema de optimización sin restricciones.
un problema de optimización sin restricciones.
Se llaman puntos
de silla a aquellos puntos 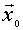 que anulan el gradiente
de la función objetivo, pero que no son máximos ni mínimos.
que anulan el gradiente
de la función objetivo, pero que no son máximos ni mínimos.
Un ejemplo de punto de silla (al que se tiende a reducir el concepto de punto de silla, por abuso de lenguaje) es:
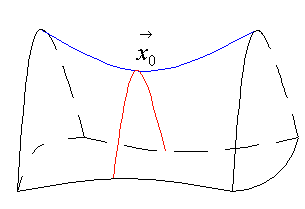
Obsérvese que en 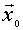 se anula el gradiente de
se anula el gradiente de 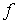 y que, en cambio,
y que, en cambio, 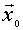 es máximo respecto de una variable y mínimo respecto de la otra.
es máximo respecto de una variable y mínimo respecto de la otra.
Restricción saturada
Definición:
Se dice que en un punto se satura una restricción o que dicha restricción está saturada o activa en ese punto, cuando en ese punto se satisface la restricción con igualdad.
Ejemplo:
El punto (3,1) satisface la restricción 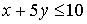 , pero no la satura.
, pero no la satura.
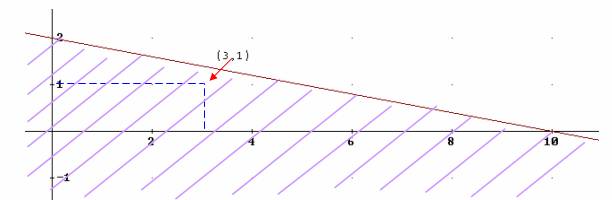
En cambio, el punto (3,1) satura la restricción 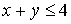
Semiespacios en ℜn
Definición:
Un semiespacio es cada una de las partes en que un hiperplano divide un espacio.
Ejemplos:
- Semiespacio positivo cerrado { x ∈ ℜn | at x ≥ k }
- Semiespacio positivo abierto { x ∈ ℜn | at x > k }
- Semiespacio negativo cerrado { x ∈ ℜn | at x ≤ k }
- Semiespacio negativo abierto { x ∈ ℜn | at x < k }
Propiedades:
Un semiespacio es un conjunto convexo.
Teorema de separación de conjuntos convexos
Teorema:
Sean A y B dos conjuntos convexos disjuntos (A B= O), entonces se
cumple que existe un hiperplano H que los separa (de manera que A pertenece a
uno de los semiespacios y B al otro).
B= O), entonces se
cumple que existe un hiperplano H que los separa (de manera que A pertenece a
uno de los semiespacios y B al otro).
Ejemplo:
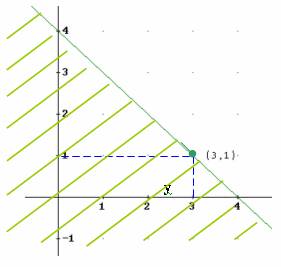
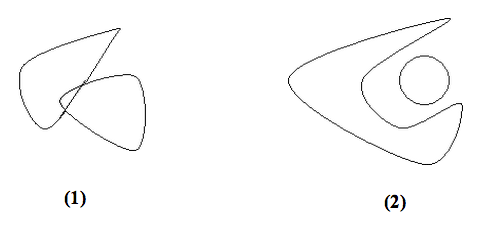
Observemos que separar dos conjuntos no es, en general, posible si A y B no son disjuntos (1) o si uno de los dos no es convexo (2).
Teorema de Weierstrass
Enunciado:
Toda función continua sobre dominio compacto alcanza máximo y mínimo globales.
Intuitivamente:
Observemos que aún siendo continua no tiene máximos ni mínimos:
No obstante, si la definimos sobre un intervalo cerrado (y acotado) automáticamente alcanza máximo y mínimo globales.
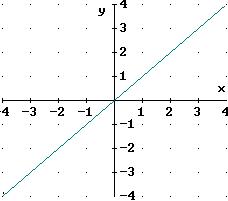
Sea, por ejemplo,
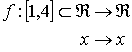
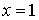 mínimo global
mínimo global
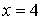 máximo global
máximo global
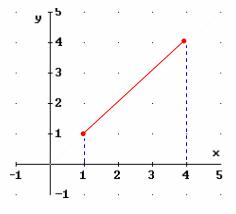
Observemos también que el intervalo debe ser cerrado, porque si uno de los extremos es abierto, ya no alcanzará el óptimo.
Es decir,
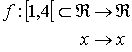
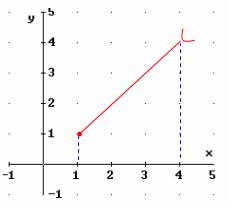
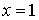 mínimo global
mínimo global
Notemos que 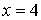 ya no es máximo
global, puesto que ya no pertenece al dominio de la función,
ni hay otro máximo (Podríamos pensar que el nuevo máximo fuese 3,999999,
pero es fácil caer en la cuenta de que podríamos añadir un 9 y obtener un
máximo mejor: 3,9999999 ).
ya no es máximo
global, puesto que ya no pertenece al dominio de la función,
ni hay otro máximo (Podríamos pensar que el nuevo máximo fuese 3,999999,
pero es fácil caer en la cuenta de que podríamos añadir un 9 y obtener un
máximo mejor: 3,9999999 ).
Nota:
- El teorema se refiere sólo a óptimos GLOBALES, no dice nada de óptimos locales.
- El teorema se refiere a la existencia, no dice si hay uno o varios.
Gráficamente:


 compacto
compacto 
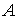
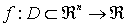 D
D  D
D