Capítol 5 Generació de gràfics

5.1 Elements bàsics

Quan fem un gràfic necessitem tenir clars cinc elements bàsics:

Dades d’on volem extreure la informació que volem representar
Projecció estètica, és a dir, la relació concreta entre les variables que volem representar; bàsicament decidir una x i una y, però també variables que agrupen
Objecte geomètric que volem que representi la informació anterior (punts, cercles, barres, caixes, línies, etc.)
Coordenades i escales que han de donar al gràfic els elements necessaris per tal que pugui ser interpretat
Etiquetes i títols que donin un context interpretatiu final al gràfic

La llibreria ggplot2 està dissenyada per implementar l’anomenada “gramàtica dels gràfics” creada per Leland Wilkinson i que es basa precisament en els elements que acabem de presentar.

Així com en la llibreria bàsica vèiem que la major part dels paràmetres d’un gràfic eren, de fet, arguments d’una sola funció com plot() que havíem d’anar afegint, ggplot2 organitza la feina de construir un gràfic per tasques que van afegint nivells o capes als gràfics, cadascuna de les quals té un sentit estructural.

5.2 Llibreria `ggplot2`

Podem dividir les tasques de construir un gràfic en tres blocs:

La funció bàsica ggplot(), amb què comencen tots els gràfics. En aquesta funció s’estableixen els dos primers elements bàsics d’un gràfic:
- Les dades a partir de les quals volem construir un gràfic
- La projecció estètica que implica la relació entre les variables que volem representar gràficament
La família de funcions geom_ que serveixen per triar l’objecte geomètric triat per representar el gràfic: punts, barres, caixes, línies, etc.
Funcions de les famílies scale_ i theme_ (entre altres) que permeten ajustar coordenades, escales, títols, etiquetes i altres elements de context.

ggplot2 implica sempre seguir l’ordre que acabem de presentar a l’hora de crear un gràfic. Per tant, a continuació seguirem aquest ordre per crear gràfics.

5.3 Creació d’un gràfic

Per treure profit de la potència de la llibreria ggplot2 és important fer-la servir pensant que la forma d’escriure el codi per crear un gràfic ens ajudi a estructurar la forma en què pensem en el gràfic.

5.3.1 Dades i projecció estètica

Tot gràfic amb ggplot2 comença amb la funció ggplot(), que té dos arguments generals:

data: on especifiquem les dades a partir de les quals volem crear un gràfic
mapping: que té com a argument la funció aes(), que especifica la projecció estètica, és a dir, quines variables volem relacionar i com les volem relacionar

Si fem servir les dades de resultats electorals municipals als barris de Barcelona de 2015 i volem relacionar el percentatge d’aturats dels barris amb els resultats del PSC, ho farem així:

library(tidyverse)
result <- read_csv("data/resultats_municipals_2015_barris.csv", 
                   locale = locale(encoding="ISO-8859-1"))

## Rows: 73 Columns: 19
## ── Column specification ──────────────────────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr  (3): districte, barri, partit.mes.votat
## dbl (16): districte_codi, barri_codi, BeComu, CiU, Cs, ERC, PSC.CP, PP, CUP.PA, Altres, Blancs, Nuls, participacio_muni_20...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

p <- ggplot(
  data = result,
  mapping = aes(x = atur, y = PSC.CP)
)
p

5.3.2 Objecte geomètric

Fixem-nos-hi bé. La Figura és incompleta perquè encara no hem especificat cap objecte geomètric que representi la projecció estètica que hem especificat entre les dues variables en qüestió. Això és una diferència important respecte de la funció plot() de la llibreria bàsica. En el cas que ens ocupa, si volem representar la relació entre atur i vot al PSC amb punts, triarem la funció de la família geom_ corresponent als punts: geom_point():

p + geom_point()

Si volem fer canvis en la forma, color, mida o qualsevol altra característica dels objectes geomètrics que volem fer servir, ho farem dins de la funció específica geom_:

p + geom_point(
  color = "red", 
  size = 2, 
  shape = 21
)

5.3.2.1 Afegim una tercera variable categòrica

Imaginem que volem introduir una tercera variable en un gràfic: volem saber si la relació entre atur i participació té relació amb el partit més votat a cada barri. Com que el partit més votat és una variable categòrica, això ho podem fer de dues maneres diferents:

Representant el partit més votat com un color dins del gràfic de punts
Creant un gràfic diferent per a cada partit més votat

5.3.2.1.1 Canvi de color

Si volem que la variable categòrica s’expressi mitjançant un color, només l’hem d’afegir als elements de projecció estètica amb colour:

ggplot(
  result,
  aes(
    x = atur,
    y= participacio_muni_2015,
    colour = partit.mes.votat)
  ) +
  geom_point()

5.3.2.1.2 Facets

Si, en canvi, volem crear un gràfic separat per a cada partit més votat, de manera que puguem veure exactament com és la relació entre atur i participació en funció del partit que guanya a cada barri, farem servir la funció facet_ en una de les seves tipologies. Si ho fem amb facet_wrap()

ggplot(result,
       aes(x = atur, y = participacio_muni_2015)) +
  geom_point() +
  facet_wrap(~partit.mes.votat)

5.3.2.1.3 Tercera variable contínua

Continuem amb el gràfic que relaciona el percentatge d’aturats amb el vot al PSC, però ara volem, a més, que els punts del gràfic de dispersió mostrin, a través de colors, els barris que participen més i els que participen menys. El percentatge de participació és una variable contínua, però hem de decidir si volem que aquesta variable es mostri com a contínua o com a factor. Darrera aquesta decisió hi ha d’haver un criteri de visualització clar per part nostra. Volem simplement que es mostri la gradació en la participació o volem que s’identifiquin grups de barris segons la seva participació de manera més clara?

Si optem per la segona opció, una possibilitat és crear una nova variable (un factor) que classifiqui els barris, per exemple, segons si es troben per sobre o per sota de la mitjana de participació, i aleshores expressar aquesta variable amb dos colors diferents:

result <- result %>% 
  mutate(part_rec = ifelse(participacio_muni_2015 < mean(participacio_muni_2015, 
                                                         na.rm = TRUE),
                           "Participació baixa",
                           "Participació alta"))

ggplot(result,
       aes(x = atur, y= PSC.CP, colour = part_rec)) +
  geom_point()

En aquest gràfic no hi ha dubte possible: els barris de color blau, que són els de més atur i més vot al PSC, són els que van participar menys, mentre que els barris amb menys atur i menys vot al PSC són més participatius.

Si, en canvi, optem per la gradació, ja no hem de crear primer una paleta de colors, com fèiem amb la llibreria bàsica, sinó que ggplot ens la crea per nosaltres. Només hem d’especificar la variable contínua que volem que sigui representada pel color:

ggplot(result, 
       aes(x = atur, y = PSC.CP)) +
  geom_point(aes(color = participacio_muni_2015))

El color per defecte és una escala de blaus, però això ho podem canviar al nostre gust amb el grup de funcions de scale_color. Per exemple, la funció scale_color_gradientn() ens permet especificar els colors de l’extrem de l’escala que desitgem:

ggplot(result, 
       aes(x = atur, y = PSC.CP)) +
  geom_point(aes(color = participacio_muni_2015)) +
  scale_color_gradientn(colors =c("blue","red"))

5.3.2.1.4 Canvi de mida

També podem decidir que, com que moltes revistes fan pagar per publicar gràfics en color, en comptes del color volem que la tercera variable es representi a través de la mida dels punts del gràfic. Per fer-ho, altre cop hem de decidir un criteri. Aquí la clau és la proporcionalitat, és a dir, que la mida dels punts han de representar alguna relació proporcional entre ells per tal que l’efecte visual sigui efectiu. Una opció molt habitual i efectiva és relacionar la mida dels punts amb el valor mitjà de la variable. Per fer-ho, retocarem el paràmetre que regula la mida dels punts, i ho farem directament dividint la variable de participació per la seva mitjana, de manera que la mida dels punts projecti la ratio de cada observació respecte de la mitjana:

ggplot(result,aes(x = atur, y = PSC.CP)) +
  geom_point(aes(size = participacio_muni_2015))

Finalment, potser la tercera variable que volem representar és un factor amb un valor únic per a cada observació, com pot ser el nom de cada barri. Podem representar el nom del barri al costat de cada punt per tal que el lector pugui identificar de seguida els barris on la relació entre atur i vot al PSC és més acusada o menys. Per fer-ho, haurem d’afegir text al gràfic:

ggplot(result,aes(x = atur, y = PSC.CP)) +
  geom_point() +
  geom_text(aes(label = barri))

Veiem que així, el gràfic no es pot llegir de cap manera, per dues raons: el text dels noms de barri és encara massa gran (tot i que ja havíem retocat l’argument cex que té valor 1 per defecte) i el text se sobreposa al punt. Resoldrem els dos problemes:

ggplot(result, aes(x = atur, y = PSC.CP)) +
  geom_point() +
  geom_text(
    aes(label = barri),
    check_overlap = TRUE,
    size = 3,
    nudge_y = 0.2,
    vjust = 0
  )

5.3.3 Coordenades i escales

Fem un gràfic que relacioni la renda disponible de cada barri amb el vot que va rebre el PSC. Imaginem que volem que l’eix vertical (y) tingui només dues marques, al 10 i al 20. Els detalls sobre les escales es regulen per funcions separades de la funció principal, altre cop. En aquest cas, el grup de funcions que comencen per scale_ regulen totes les escales possibles. En el cas que ens ocupa, ho farem així:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  scale_y_continuous(breaks = c(seq(0, 20, 10)))

5.3.3.1 Coordenades

Per altra banda, a més de l’escala, les coordenades també són un element que pot ajudar a la interpretació d’un gràfic. Les coordenades són punts de referència que ajuden a relacionar els punts representats amb l’escala dels eixos. Els gràfics per defecte de ggplot2 ja porten una graella incorporada que és de gran ajuda. Si, tanmateix, les volem eliminar, haurem de canviar el tema (theme) del gràfic i treure-les:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  scale_y_continuous(breaks = c(seq(0, 20, 10))) +
  theme(panel.grid.major = element_blank(), 
        panel.grid.minor = element_blank())

Si, a més, volem que hi hagi alguna línia que marqui una referència concreta, com ara un valor mitjà, podrem afegir-la mitjançant l’addició d’un altre element geomètric, com ara una línia vertical (geom_vline) o horitzontal (geom_hline):

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  scale_y_continuous(breaks = c(seq(0, 20, 10))) +
  theme(panel.grid.major = element_blank(), 
        panel.grid.minor = element_blank()) +
  geom_vline(aes(xintercept = mean(renda_100)), 
             linetype = "dashed",
             color = "red")

5.3.4 Títols i etiquetes

Finalment, la darrera cosa que hem de polir és la informació de context que acabi de donar claus d’interpretació del gràfic. Hi ha tres tipus bàsics diferents d’informació de context:

Les etiquetes dels eixos
Les guies o llegendes
El títol del gràfic

5.3.4.1 Etiquetes dels eixos

Hi ha una funció que permet afegir tota la informació necessària sobre títols i eixos a un gràfic amb ggplot: la funció labs(). En primer lloc, ens permet incloure els títols dels eixos:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC"
  )

Després, la mateixa funció podem també incloure, títols, subtítols i fins i tot peus de pàgina al gràfic:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  )

### Afegim rectes de regressió

Quan estem projectant la relació entre dues variables contínues, típicament és d’interès conèixer fins a quin punt les dues variables estan correlacionades. Això també ho podem representar gràficament amb una recta de regressió (lineal o no lineal). Per fer-ho, farem servir la funció geom_smooth(). Si volem que la relació entre les dues variables sigui una recta (per tant, aplicar-hi un mètode lineal), l’argument method tindrà com a valor lm (de linear model). En cas que vulguem representar-hi una funció no lineal, prendrà el valor loess. Aplicat al cas anterior:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  geom_smooth(method="lm") +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  )

## `geom_smooth()` using formula = 'y ~ x'

O aplicant-hi una funció no lineal com la locally estimated scatterplot smoothing (loess):

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  geom_smooth(method="loess") +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  )

## `geom_smooth()` using formula = 'y ~ x'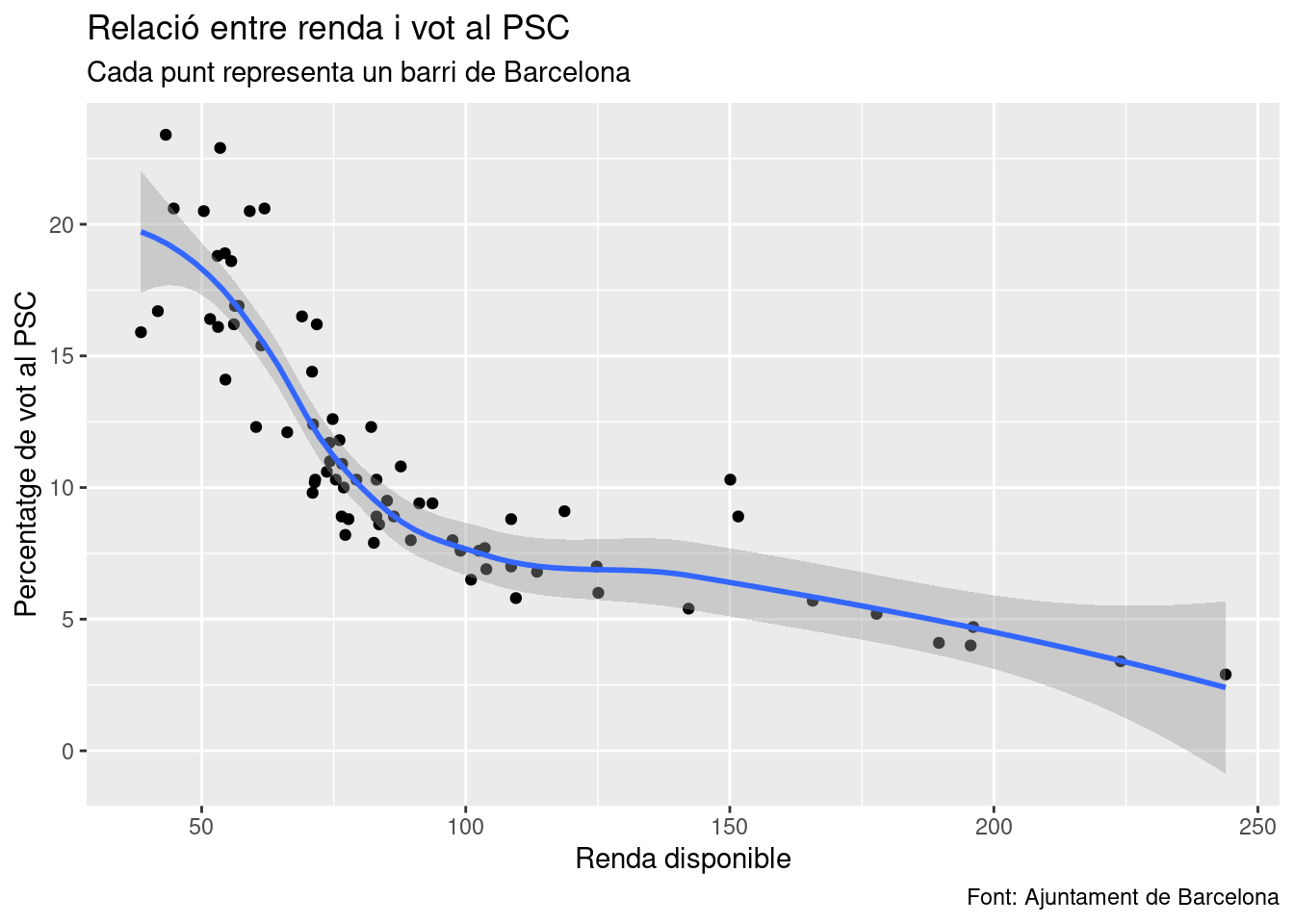

### Escales

De vegades, la representació gràfica d’una variable contínua en la seva escala natural és problemàtica perquè presenta una distribució molt desequilibrada en les observacions. Variables com la població de municipis o la renda en són exemples típics. Per veure-ho, farem servir unes dades corresponents a informació demogràfica per municipis de Catalunya:

censals <- read_delim(
  "data/dades_censals_municipis.csv",
  delim = "\t",
  locale = locale(encoding = "ISO-8859-1", 
                  decimal_mark = ",")
)

## Rows: 946 Columns: 29
## ── Column specification ──────────────────────────────────────────────────────────────────────────────────────────────────────
## Delimiter: "\t"
## chr  (2): municipi, Comarca
## dbl (26): provincia, codi, pob.1999, pob.2000, Immig.2000, pob.2001, Immig.2001, pob.2002, Immig.2002, pob.2003, Immig.200...
## lgl  (1): Immig.1999
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

censals

## # A tibble: 946 × 29
##    provincia  codi municipi    pob.1…¹ Immig…² pob.2…³ Immig…⁴ pob.2…⁵ Immig…⁶ pob.2…⁷ Immig…⁸ pob.2…⁹ Immig…˟ pob.2…˟ Immig…˟
##        <dbl> <dbl> <chr>         <dbl> <lgl>     <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
##  1         8     1 Abrera         7728 NA         8177    2.8     8454    3.56    8823    4.48    9166    5.74    9422    6.11
##  2         8     2 Aguilar de…     213 NA          213    0.47     208    0        215    0.93     224    1.34     230    0.87
##  3         8     3 Alella         8176 NA         8413    3.47    8614    4.3     8796    5.34    8847    6.5     8831    6.94
##  4         8     4 Alpens          266 NA          264    3.41     274    4.38     277    5.78     287    6.27     290    5.17
##  5         8     5 Ametlla de…    5294 NA         5697    4.46    5910    5.2     6328    6.16    6757    7.81    7111    8.9 
##  6         8     6 Arenys de …   12345 NA        12610    3.78   12819    4.69   13107    6.5    13431    7.92   13428    8.25
##  7         8     7 Arenys de …    6037 NA         6242    2.37    6512    3.15    6827    4.03    6977    4.72    7190    5.24
##  8         8     8 Argençola       195 NA          196    0.51     188    0.53     195    1.03     202    1.98     209    2.87
##  9         8     9 Argentona      9213 NA         9482    1.29    9791    1.69   10056    2.43   10302    2.76   10403    2.85
## 10         8    10 Artés          4293 NA         4368    0.64    4443    1.06    4552    1.93    4696    2.9     4830    4.43
## # … with 936 more rows, 14 more variables: pob.2005 <dbl>, Immig.2005 <dbl>, pob.2006 <dbl>, Immig.2006 <dbl>,
## #   pob.2007 <dbl>, Immig.2007 <dbl>, pob.2008 <dbl>, Immig.2008 <dbl>, pob.2009 <dbl>, Immig.2009 <dbl>,
## #   `Codi Comarca` <dbl>, Comarca <chr>, Densitat <dbl>, PIB.habitant <dbl>, and abbreviated variable names ¹pob.1999,
## #   ²Immig.1999, ³pob.2000, ⁴Immig.2000, ⁵pob.2001, ⁶Immig.2001, ⁷pob.2002, ⁸Immig.2002, ⁹pob.2003, ˟Immig.2003, ˟pob.2004,
## #   ˟Immig.2004

Imaginem que volem veure si hi ha una relació entre la grandària poblacional dels municipis i el seu percentatge de població immigrada. Si ho fem posant la variable pob.2000 a escala natural, la seva distribució tan desigual entre els municipis no ens permet veure res al gràfic:

ggplot(censals, 
       aes(x = pob.2000, y = Immig.2000)) +
  geom_point()

Una solució (la més habitual) és transformar aquesta variable a escala logarítmica, especificant amb la funció scale_x_log10() que és l’eix x el que volem transformar:

ggplot(censals, 
       aes(x = pob.2000, y = Immig.2000)) +
  geom_point() +
  scale_x_log10()

5.4 Histogrames, gràfics de barres i de línies

Uns dels gràfics més utilitzats són aquells que descriuen freqüències o especifiquen la posició d’una variable categòrica respecte d’una quantitat concreta. Aquests tipus de gràfics sovint representen aquesta informació amb barres o línies. Com a regla general, quan la variable que volem representar és contínua en representarem la distribució mitjançant un histograma, mentre que quan tractem amb variables categòriques treballarem amb gràfics de barres.

La diferència entre un histograma i un gràfic de barres no sempre és coneguda, però és molt important. En un histograma, l’àrea dels rectangles que conformen les barres és una representació proporcional a la quantitat que el gràfic està representant, de manera que la base i l’alçada han de tenir, per força, unes unitats conegudes. En canvi, en els gràfics de barres l’important és només l’alçada, és a dir, el punt de l’eix y que aquesta alçada està indicant en el gràfic, mentre que l’amplada de la seva base només respon a criteris estètics. Per això, un gràfic de barres sempre es pot representar com un gràfic de línies i viceversa. Ara en mostrarem exemples.

5.4.1 Histogrames

Si volem mostrar com es distribueix la variable que indica els percentatges de població immigrada per a l’any 2000, farem servir un histograma:

ggplot(censals, aes(Immig.2000)) +
  geom_histogram() +
  labs(
    x="Percentatge de població immigrada, any 2000",
    y="Freqüència de municipis"
  )

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.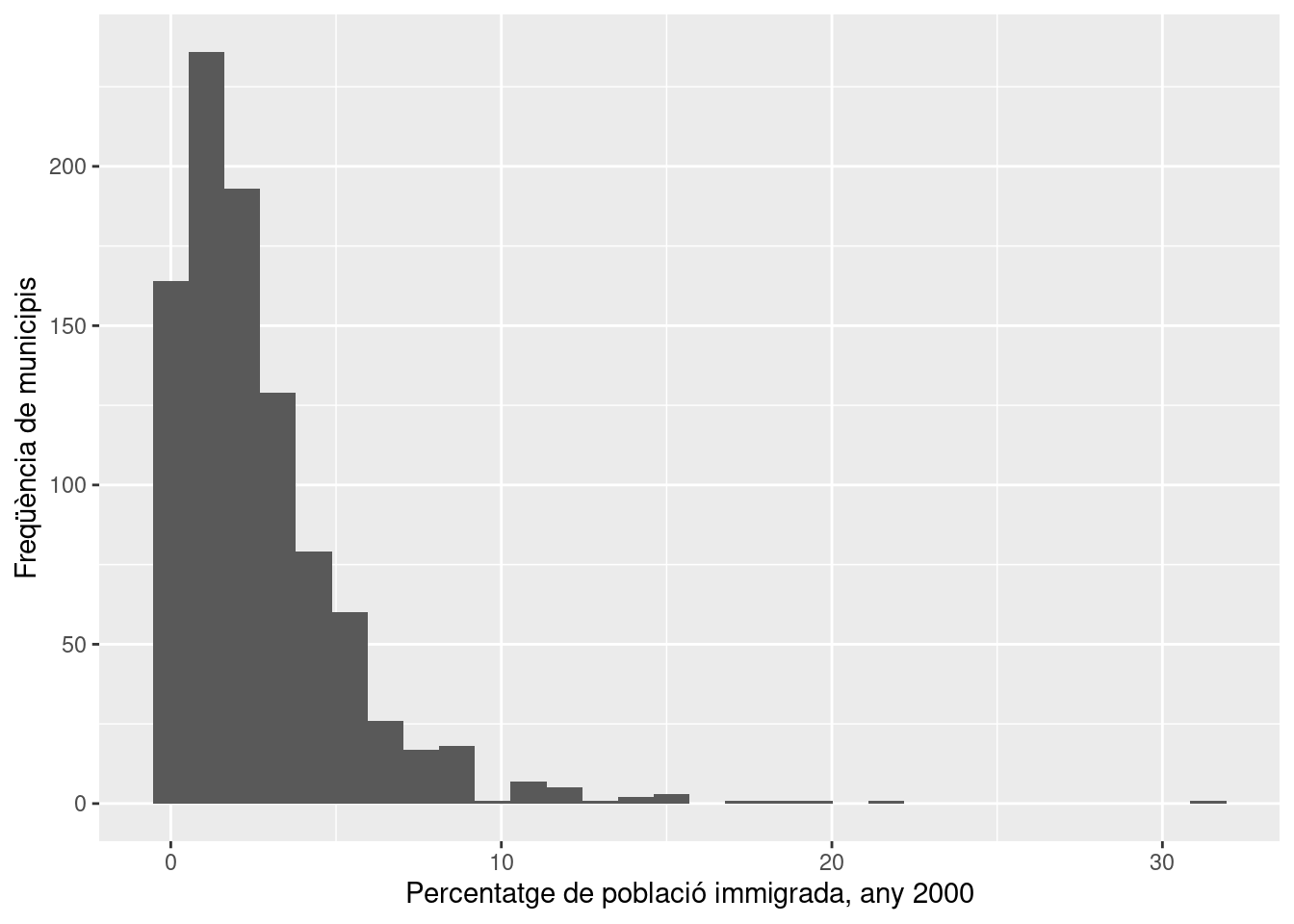

Aquest és el seu aspecte per defecte. Si volem que es vegin els contorns dels rectangles, podem afegir alguns valors als arguments de dins de geom_histogram() relacionats amb el contorn de les barres (colour) i amb el color de les barres (fill):

ggplot(censals, aes(Immig.2000)) +
  geom_histogram(colour = "black", 
                 fill="white") +
  labs(
    x="Percentatge de població immigrada, any 2000",
    y="Freqüència de municipis"
  )

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Fixem-nos que aquest histograma mostra el recompte de municipis que presenten percentatges de població immigrada de nivells diversos. Els diversos nivells de població es mostren en l’eix horitzontal (x), mentre que la quantitat de municipis en l’eix vertical (y). Així, veiem que hi ha una mica més de 150 municipis que tenen percentatges d’immigrants molt propers a zero (entre 0 i 1%), mentre que molt pocs tenen percentatges superiors al 10%.

Com dèiem més amunt, els rectangles de l’histograma tenen una àrea determinda que està en funció de la seva base i la seva alçada. Podem canviar aquesta àrea canviant el percentatge que serveix per dividir els rectangles. Per exemple, si en comptes de fer un rectangle per a cada punt percentual, en volem fer un per cada dos punts, ho farem amb l’argument binwidth, donant-li el valor 2, que farà que els rectangles siguin més amples i que canviïn les freqüències:

ggplot(censals, aes(Immig.2000)) +
  geom_histogram(colour = "black", 
                 fill = "white", 
                 binwidth = 2) +
  labs(
    x="Percentatge de població immigrada, any 2000",
    y="Freqüència de municipis"
  )

Si, finalment, volem afegir una línia vertical que mostri el valor mitjà del percentage de població immigrada als municipis de Catalunya l’any 2000, ho podem fer amb la funció geom_vline():

ggplot(censals, aes(Immig.2000)) +
  geom_histogram(colour = "black", fill = "white", binwidth = 2) +
  geom_vline(
    aes(xintercept = mean(Immig.2000, na.rm = TRUE)), 
    colour="red",
    linetype="dashed"
  ) +
  labs(
    x="Percentatge de població immigrada, any 2000",
    y="Freqüència de municipis"
  )

5.4.2 Boxplots

Un altre gran gràfic per representar distribucions és el boxplot, que també es pot fer amb ggplot2. A continuació mostrem la distribució de la població immigrada el 2009 dels municipis per províncies:

ggplot(censals,
       aes(x = as.factor(provincia), y = Immig.2009)) +
  geom_boxplot() +
  labs(fill = "Província") +
  scale_x_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona")) +
  scale_fill_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona")) +
  labs(
    x="",
    y="Distribució de població immigrada")

Si volguéssim que els diferents gràfics de caixa ens apareguessin ordenats segons els nivells de població immigrada, ho podem fer fent servir la funció que ja coneixem: reorder():

ggplot(censals,
       aes(x = reorder(as.factor(provincia),Immig.2009), y = Immig.2009)) +
  geom_boxplot() +
  labs(fill = "Província") +
  scale_x_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona")) +
  scale_fill_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona")) +
  labs(
    x="",
    y="Distribució de població immigrada")

5.4.3 Gràfics de barres

Més amunt comentàvem que els gràfics de barres són indicats per representar recomptes o quantitats referides a variables categòriques. Per treballar-hi, farem servir

vg <- read_csv("data/Victimes_de_violencia_domestica.csv")

## Rows: 240 Columns: 8
## ── Column specification ──────────────────────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr (5): Trimestre, Edat, Gènere, Tipus, Àmbit
## dbl (3): Any, Víctimes ateses, Víctimes mortals
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Un primer exemple podria ser voler reprentar, en les dades amb què estem treballant, quants municipis té cada província. Com que això és un recompte, farem servir stat="count" a geom_bar() (tot i que aquest és el seu valor per defecte i, per tant, si no hi posem res també ens funcionarà):

ggplot(censals, aes(x = as.factor(provincia))) +
  geom_bar(stat = "count") +
  labs(
    x="",
    y="Nombre de municipis"
  ) +
  scale_x_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona"))

Fent servir l’argument stat="count" obtenim, en efecte, un recompte del nombre de municipis de cada província. És important notar que en l’argument principal de ggplot() només especifiquem un valor (x) i no especifiquem un valor de y, perquè el que volem amb el gràfic és justament representar el recompte de casos (municipis) de cadascuna de les categories (províncies).

Altres cops, però, no volem representar la freqüència absoluta de cada categoria de la variable sinó les proporcions o percentatges. Per fer-ho, haurem de dur a terme dues operacions bàsiques. En primer lloc, li haurem d’especificar a ggplot() que a l’eix y voldrem les dades reprsentades com a proporcions. Això ho aconseguim mitjançant l’expressió y = ..prop.. a dins de aes(). Fixem-nos que el que estem fent aquí és definir com volem l’eix vertical (y). La segona operació bàsica és que hem d’afegir group="x" també a dins de aes(). Aquest argument és molt important, perquè determina que les proporcions siguin calculades sobre el total dels valors de totes les categories de la variable, ja que el comportament per defecte de geom_bar() seria agrupar per cada categoria. De fet, l’argument group el podem fer servir per agrupar per qualsevol altra variable categòrica que ens interessi.

ggplot(censals, aes(x = as.factor(provincia), y = ..prop.., group = "x")) +
  geom_bar(stat = "count") +
  labs(
    x="",
    y="Nombre de municipis"
  ) +
  scale_x_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona"))

Fixem-nos què passaria si no féssim servir group="x":

ggplot(censals, aes(x = as.factor(provincia), y = ..prop..)) +
  geom_bar(stat = "count") +
  labs(
    x="",
    y="Nombre de municipis"
  ) +
  scale_x_discrete(labels = c("Barcelona", "Girona", "Lleida", "Tarragona"))

Això passa perquè l’argument group és un argument per anul·lar el comportament per defecte, que és agrupar per la variable x per tal de comptar per separat el nombre de files per a cada nivell de la variable x, que en el nostre cas és la província. Per exemple, aquí, com hem vist, el comportament per defecte de ggplot és donar-nos el nombre de municipis de Barcelona, Girona, Lleida i Tarragona.

Ara bé, quan volem proporcions (o percentatges), els percentatges de municipis de cada província s’han de calcular sobre el total de municipis de Catalunya. Per això, en el gràfic que acabem de fer, ggplot ha entès que havia de calcular la proporció de municipis de Barcelona dins de la categoria Barcelona, que naturalment és el 100%, i això passa amb cada província. Aleshores, l’argument group="x" el que fa és anul·lar el comportament per defecte i les proporcions seran calculades sobre el total de la variable x.

Moltes vegades, però, volem representar no recomptes sinó senzillament un valor específic per a cada categoria de la variable categòrica. Un exemple seria fer un gràfic que reprentés la població mitjana dels municipis de cada província catalana per a l’any 2001. Per fer-ho, combinarem la transformació de les dades, primer, per, després, fer el gràfic amb la funció geom_bar():

mitjanes <- censals %>% 
  group_by(provincia) %>% 
  summarise(mean_pob = mean(pob.2001, 
                            na.rm = TRUE)) %>% 
  mutate(prov_rec = recode(provincia,
                            "8" = "Barcelona",
                            "17" = "Girona",  
                            "25" = "Lleida", 
                            "43" = "Tarragona"))

mitjanes

## # A tibble: 4 × 3
##   provincia mean_pob prov_rec 
##       <dbl>    <dbl> <chr>    
## 1         8   15449. Barcelona
## 2        17    2623. Girona   
## 3        25    1580. Lleida   
## 4        43    3345. Tarragona

ggplot(mitjanes,
       aes(prov_rec,mean_pob)) +
  geom_bar(stat="identity")

Podem fer que en el gràfic les barres apareguin ordenades a partir de la variable quantitativa (per defecte ho estàn alfabèticament per les categories del factor, en aquest cas):

ggplot(mitjanes,
       aes(reorder(prov_rec, -mean_pob),mean_pob)) +
  geom_bar(stat="identity")

Fixeu-vos que per reordenar les barres fem servir la funció reorder(). Per defecte, el seu ordre serà ascendent (de més petit a més gran), però això es pot invertir posant un signe negatiu (-) davant de la variable contínua dins de la funció reorder().

També podem girar els eixos amb coord_flip():

ggplot(mitjanes,
       aes(reorder(prov_rec, -mean_pob),mean_pob)) +
  geom_bar(stat="identity") +
  coord_flip()

Fixeu-vos que fem servir l’argument stat="identity" dins de geom_bar() perquè el que volem és que les barres representin exactament (“idènticament”) el valor de la població mitjana corresponent a cada província.

Imaginem ara que volem representar el nivell de població mitjana de cada província en dos anys diferents, 2001 i 2009. Fixem-nos que per representar en un gràfic el canvi de població mitjana en els dos anys haurem de canviar l’estructura de les dades. Comencem seleccionant (select()) només les variables que ens interessen, i després transformem les dades:

censals_noves <- censals %>% 
  select(municipi, provincia, pob.2001, pob.2009, Comarca) %>%
  as.tibble()
censals_noves

## # A tibble: 946 × 5
##    municipi                provincia pob.2001 pob.2009 Comarca        
##    <chr>                       <dbl>    <dbl>    <dbl> <chr>          
##  1 Abrera                          8     8454    11521 Baix Llobregat 
##  2 Aguilar de Segarra              8      208      257 Bages          
##  3 Alella                          8     8614     9397 Maresme        
##  4 Alpens                          8      274      311 Osona          
##  5 Ametlla del Vallès (L')         8     5910     7949 Vallès Oriental
##  6 Arenys de Mar                   8    12819    14627 Maresme        
##  7 Arenys de Munt                  8     6512     8190 Maresme        
##  8 Argençola                       8      188      240 Anoia          
##  9 Argentona                       8     9791    11633 Maresme        
## 10 Artés                           8     4443     5433 Bages          
## # … with 936 more rows

cens_g <- censals_noves %>%
  gather(key ="any",value ="poblacio", -municipi, -provincia, -Comarca) %>% 
  separate(any, into=c("variable", "any"))
cens_g

## # A tibble: 1,892 × 6
##    municipi                provincia Comarca         variable any   poblacio
##    <chr>                       <dbl> <chr>           <chr>    <chr>    <dbl>
##  1 Abrera                          8 Baix Llobregat  pob      2001      8454
##  2 Aguilar de Segarra              8 Bages           pob      2001       208
##  3 Alella                          8 Maresme         pob      2001      8614
##  4 Alpens                          8 Osona           pob      2001       274
##  5 Ametlla del Vallès (L')         8 Vallès Oriental pob      2001      5910
##  6 Arenys de Mar                   8 Maresme         pob      2001     12819
##  7 Arenys de Munt                  8 Maresme         pob      2001      6512
##  8 Argençola                       8 Anoia           pob      2001       188
##  9 Argentona                       8 Maresme         pob      2001      9791
## 10 Artés                           8 Bages           pob      2001      4443
## # … with 1,882 more rows

mitjanes <- cens_g %>% 
  group_by(provincia, any) %>% 
  summarise(mean_pob = mean(poblacio, na.rm = TRUE)) %>% 
  mutate(prov_rec = recode(provincia,
                           "8" = "Barcelona",
                           "17" = "Girona", 
                           "25" = "Lleida", 
                           "43" = "Tarragona"))

## `summarise()` has grouped output by 'provincia'. You can override using the `.groups` argument.

mitjanes

## # A tibble: 8 × 4
## # Groups:   provincia [4]
##   provincia any   mean_pob prov_rec 
##       <dbl> <chr>    <dbl> <chr>    
## 1         8 2001    15449. Barcelona
## 2         8 2009    17646. Barcelona
## 3        17 2001     2623. Girona   
## 4        17 2009     3384. Girona   
## 5        25 2001     1580. Lleida   
## 6        25 2009     1889. Lleida   
## 7        43 2001     3345. Tarragona
## 8        43 2009     4390. Tarragona

ggplot(mitjanes, 
       aes(prov_rec, mean_pob, fill = any)) +
  geom_bar(stat = "identity")

Si preferim que les barres corresponents a cada any apareguin de costat en comptes de superposades, farem servir l’argument position_dodge():

ggplot(mitjanes, aes(prov_rec, mean_pob, fill = any)) +
  geom_bar(stat = "identity", position = position_dodge())

Com que aquests colors per defecte potser no ens convencen, podem fer-ho tot en una escala de grisos:

ggplot(mitjanes, 
       aes(prov_rec, mean_pob, fill = any)) +
  geom_bar(stat = "identity", position = position_dodge()) +
  scale_fill_grey()

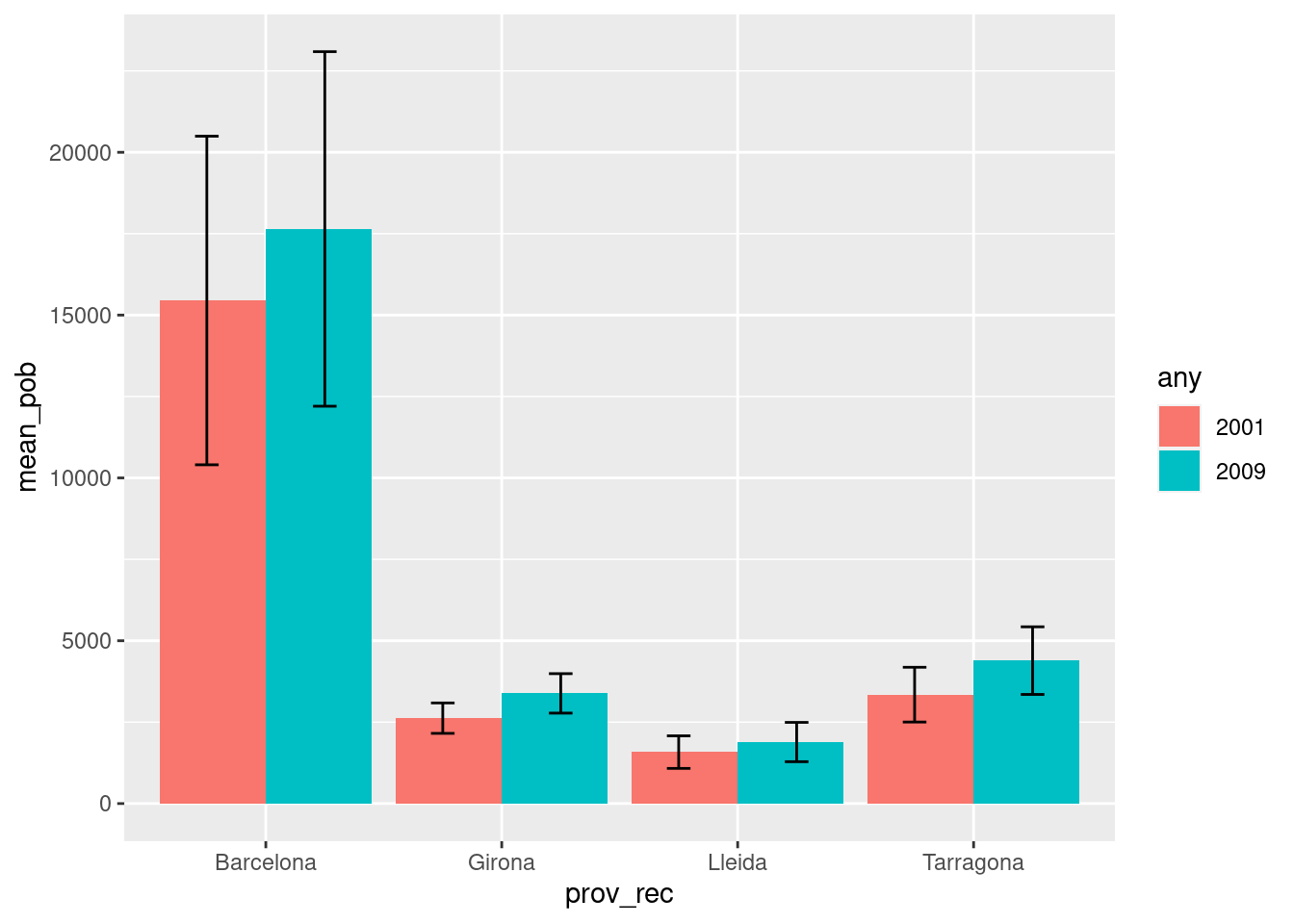
De vegades ens convé representar, juntament amb les barres, el grau de variació de les dades que volem mostrar (amb barres d’error). En el cas de les dades que ara estàvem representant, potser ens convindria representar, juntament amb la mitjana de població, una barra indicant el grau de variació, per exemple la desviació estàndard. Començarem creant una variable en les dades que indiqui la desviació respecte de la mitjana:

mitjanes <- cens_g %>% 
  group_by(provincia, any) %>% 
  summarise(
    mean_pob = mean(poblacio, na.rm = TRUE),
    se = sd(poblacio,na.rm = TRUE)/sqrt(length(poblacio))) %>% 
  mutate(prov_rec = recode(provincia,
                           "8" = "Barcelona",
                           "17" = "Girona", 
                           "25" = "Lleida", 
                           "43" = "Tarragona"))

## `summarise()` has grouped output by 'provincia'. You can override using the `.groups` argument.

ggplot(mitjanes , 
       aes(prov_rec, mean_pob, fill = any)) +
  geom_bar(stat ="identity", position = position_dodge()) +
  geom_errorbar(
    aes(ymin=mean_pob-se, ymax=mean_pob+se),
    width=.2,
    position = position_dodge(1)
  )

5.4.4 Gràfics de línies

La mateixa informació que el gràfic anterior es pot representar amb gràfics de línies. Primer, podem agrupar les línies per any. És a dir, fem que cada línia agrupi totes les observacions d’un sol any i les connecti (amb l’argument group):

ggplot(mitjanes, 
       aes(prov_rec, mean_pob, 
           group = any, 
           colour = any)) +
  geom_line()

Si en comptes de representar les províncies a l’eix horitzontal preferim representar-hi els anys i, en canvi, que cada província apareixi identificada per una sola línia, podem jugar amb els colors:

ggplot(mitjanes, aes(any, mean_pob, 
                     group = prov_rec, 
                     colour = prov_rec)) +
  geom_line() +
  geom_point() +
  labs(
    x = "",
    y = "Població mitjana",
    colour = "Província")

També ho podem representar separadament per província i afegir les barres de l’error estàndard:

ggplot(mitjanes, aes(any, mean_pob, 
                     group="x")) +
  geom_line() +
  geom_point() +
   geom_errorbar(
     aes(ymin = mean_pob-se, ymax=mean_pob+se),
     width = .05,
     position = position_dodge(1)
    ) +
  facet_wrap(~prov_rec,
                 scales = "free_y") +
  labs(
    x = "",
    y = "Població mitjana")

Tingueu en compte algunes coses del gràfic anterior. Fixeu-vos que hem hagut d’especificar que group="x". Això és necessari a l’hora de fer gràfics de línies per fer saber a ggplot quins punts ha d’unir amb una línia. Quan són tots els punts del gràfic, aleshores group="x". Ja veurem altres casos en què aquest argument pren el nom d’una variable categòrica. La segona cosa que hem de tenir en compte és que l’eix vertical de cada facet està en una escala diferent. Això ho hem aconseguit amb l’argument scales de la funció facet_wrap().

5.5 Els temes

ggplot2 permet una flexibilitat enorme per als gràfics amb R, i una d’elles és la capacitat per ajustar els elements estètics de forma relativament senzilla. Per això hi ha un conjunt de funcions ja creades que permeten fer canviar molts elements de l’estètica d’un gràfic a la vegada. Si continuem amb el gràfic anterior, el tema per defecte veiem que estableix un rerefons gris amb una graella de línies blanques que ajuden a la interpretació. A més, les etiquetes de les marques són de color gris, mentre que els títols dels eixos i del gràfic són de color negre o d’un gris més fosc.

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  )

Una possibilitat és fer aquest estil més proper a la llibreria bàsica de R:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_classic()

O si el que no ens convencia era el gris de rerefons, podem fer-lo en blanc i negre:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_bw()

O potser el problema era que no era prou fosc:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_dark()

5.5.0.1 ggthemes

Si us instal·leu la llibreria ggthemes, podreu canviar encara més les característiques dels vostres gràfics amb estils preconstruïts, que us poden agradar. Per exemple, podeu generar gràfics amb els mateixos criteris estètics que les vostres publicacions de referència.

Si sou molt de The Economist:

library(ggthemes)

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_economist()

Si, en canvi, sou més de Five Thirty Eight:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_fivethirtyeight()

Potser voleu imimtar un gràfic fet amb Stata:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_stata()

O un gràfic tal i com el faria el guru de la visualització de dades Edward Tufte:

ggplot(result, aes(x = renda_100, y = PSC.CP)) +
  geom_point() +
  labs(
    x = "Renda disponible",
    y = "Percentatge de vot al PSC",
    title = "Relació entre renda i vot al PSC",
    subtitle = "Cada punt representa un barri de Barcelona",
    caption = "Font: Ajuntament de Barcelona"
  ) +
  theme_tufte()

5.6 Exercicis

5.6.1 Exercici 1

Els 2 arxius següents contenen dades diferents:
- ordres_2017.csv és una base de dades que conté l’estadística oficial sobre ordres d’allunyament en casos de violència de gènere a Espanya, per partits judicials, corresponent a l’any 2017
- partits_judicials_2011.csv és una base de dades que conté informació sobre partits judicials de caràcter demogràfic

Carrega i fusiona les dues bases de dades en un sol data frame que tingui per nom dades.

Crea 4 variables noves en el nou tibble dades:

p_adoptades: percentatge d’ordres adoptades del total d’incoades
p_denegades: percentatge d’ordres denegades del total d’incoades
p_inadmeses: percentatge d’ordres inadmeses del total d’incoades
densitat: densitat de població del partit judicial

Crea un gràfic de punts que relacioni la densitat de població (a escala logarítmica) dels partits judicials amb el percentatge d’ordres adoptades. Inclou-hi una recta de regressió.
Crea un gràfic de punts que relacioni la població (a escala logarítmica) dels partits judicials amb el percentatge d’ordres adoptades. Inclou-hi una recta de regressió.
Crea un gràfic que mostri la relació entre població i percentatge d’ordres d’allunament adoptades, però mostrant aquesta relació per a cada comunitat autònoma. Com varia la relació entre població i ordres adoptades per territoris? (Inclou-hi una recta de regressió.)
Calcula per a cada comunitat autònoma, creant unes dades noves:

la mitjana del percentatge d’ordres adoptades
la desviació estàndard del percentatge d’ordres adoptades

Mostra gràficament la mitjana d’ordres d’allunyament adoptades per a cada comunitat autònoma.
Col·loca barres d’error al gràfic anterior de manera que es representi una desviació estàndard de cada punt de mitjana.
De les daes originals dades, selecciona només les observacions corresponents a Catalunya i mostra gràficament el percentatge d’ordres d’allunyament adoptades per cada partit judicial, ordenades de més a menys.

5.6.2 Exercici 2

El fitxer autonomiques_a03_Barcelona.csv conté els resultats de les eleccions al Parlament de Catalunya dels barris de Barcelona en eleccions diferents. Carrega les dades en un tibble i reorganitza-les segons els principis de tidy data, és a dir, que hi hagi una variable Candidatura i una altra Perc_vots (percentatge de vots). El nou tibble s’ha de dir auto_g.
Genera un gràfic que permeti observar l’evolució del vot mitjà de cada candiatura en les diverses eleccions. (Pista: hauràs de generar primer un nou dataframe que contingui la mitjana de vot de cada candidatura cada any.)(Pista 2: mira aquí alguns exemples de gràfics.)
A partir de les dades originals endreçades (auto_g), genera un data frame que només contingui els resultats per barri corresponents a les eleccions de 2017 i genera dos gràfics:
- Un gràfic de barres o histograma que mostri en quants barris cada candidatura fou la més votada
- Un gràfic com l’anterior però amb les dades mostrades per districte
Carrega el fitxer rfd_barcelona_2016.csv, que conté dades de renda familiar disponible dels barris de Barcelona per al 2016 i fusiona’l amb el fitxer rfd_08_15.csv, que conté les dades de renda familiar dels barris de 2008 fins a 2015.
Amb les noves dades, genera un gràfic que relacioni la població dels barris amb la seva renda femiliar disponible el 2016, en què l’eix que contingui la variable de població estigui a escala logarítmica.
Genera un gràfic que mostri, per a cada districte, l’evolució de la renda familiar disponible mitjana entre 2008 i 2016. El gràfic hauria de ser de línies.

5.6.3 Exercici 3

El fitxer arrests.csv el trobareu al Campus Virtual i conté dades sobre detencions per part de la policia de la ciutat de Toronto. Carrega les dades.
Fes un gràfic que mostri la distribució de les edat de les persones detingudes.
Fes un gràfic que mostri la distribució de l’edat de les persones detingudes però per color de pell i un altre gràfic que ho mostri per sexe. En tots dos casos, fes que el gràfic indiqui quina és l’edat mediana de cada grup.
Fes un gràfic de barres que mostri el percentatge d’individus que són deixats anar (released==Yes) i els que són portats a comissaria (released==No).
Ara fes un gràfic de barres igual que l’anterior però que et separi els percentatges per raça (colour)
Posa a prova la hipòtesi segons la qual la policia revisa un nombre més alt de bases de dades cercant antecedents (variable checks) quan la persona detinguda és negra que quan és blanca.
Genera un gràfic de línies que mostri l’evolució del nombre de persones detingudes per any.
Genera un gràfic que mostri, per a cada any, el percentatge de persones detingudes que són deixades anar (released==Yes) i no (released==No).