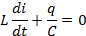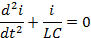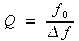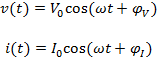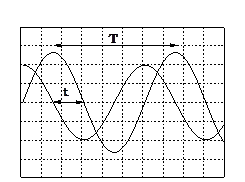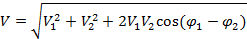AQUEST GUIÓ HA CANVIAT POTS DESCARREGAR-TE LA NOVA VERSIÓ EN PDF: Versió actual en pdf

Resum. En aquest treball es mesurarà la suma de tensions d’impedàncies connectades en sèrie.  També s’estudiarà el comportament en freqüència d’un circuit RLC sèrie, el qual presenta una ressonància.

11.1 Fonament

11.1.1 Circuit RLC sèrie; ressonància

Considereu el circuit ideal de la figura 1, format per un condensador de capacitat C, inicialment carregat amb una càrrega q_o, i per una bobina ideal (sense resistència) d’inductància L. La segona llei de Kirchhoff ens permet escriure:

on i(t) i q(t) són respectivament la intensitat de corrent i la càrrega al condensador en cada instant. Derivant l’expressió anterior i dividint per L obtenim l’equació per a la intensitat:

que és l’equació corresponent a un oscil·lador de freqüència pròpia:

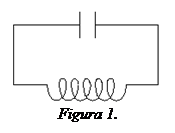I, efectivament, aquest circuit es comporta com un oscil·lador ideal: en un quart de període l’energia electrostàtica emmagatzemada al condensador es transforma per complet en energia magnètica a la bobina, de la mateixa manera que en un oscil·lador mecànic l’energia potencial el·làstica es transforma en energia cinètica. En el cas d’una bobina real, la seva resistència R fa que el comportament del circuit correspongui a un oscil·lador esmorteït, l’element dissipatiu del qual és precisament la resistència. Aquesta juga el mateix paper que el fregament en un oscil·lador mecànic, fent que l’energia es dissipi en forma de calor per efecte Joule.

Quan aleshores connectem a un generador de freqüència f l’associació en sèrie d’un condensador i una bobina, el circuit es comporta com un oscil·lador forçat i esmorteït, on el generador juga el paper de la força impulsora en el seu anàleg mecànic. En un oscil·lador forçat i esmorteït es produeix la ressonància quan la freqüència de la força impulsora coincideix exactament amb la freqüència pròpia de l’oscil·lador:

En un circuit RLC la ressonància es caracteritza per l’existència d’un pic en el valor del mòdul de l’admitància (inversa de la impedància )   per a   . A més, es produeix un canvi en el signe de la fase de l’admitància per a aquest mateix valor de la freqüència.

Per a descriure un circuit ressonant RLC sovint es fan servir dos paràmetres. El primer correspon a l’amplada del pic de ressonància, o amplada de banda, definit com l’interval de freqüències:

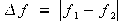	(5)

on f₁ i f₂ són els valors de la freqüència a banda i banda del pic per als quals l’admitància (o la intensitat) cau un factor . L’altre paràmetre característic és el factor de qualitat Q, que en el cas de ressonàncies estretes permet mesurar quant punxegut és el pic de la ressonància. Aleshores es pot expressar com:

11.2 Dispositiu experimental

• 1 placa de connexions
• 2 resistències (10 Ω i 100 Ω)
• 1 condensador (0.8 μF)
• 1 bobina (17 mH)
• 1 oscil·loscopi
• 1 generador de funcions
• 2 multímetres (actuant com a voltímetre i amperímetre)

11.3 Procediment experimental

11.3.1 Suma de tensions d’impedàncies connectades en sèrie

Munteu el circuit que es mostra en la figura 2. Utilitzeu la resistència de 100 Ω com a R₁ que es mantindrà fixa, mentre que l’element marcat com a Z s’anirà canviant per l'altra resistència, una bobina i un condensador. Poseu al generador de tensió una freqüència de 1,0 kHz i un voltatge d’uns 5 V.

Col·loqueu en primer lloc la resistència R en el lloc de Z i mesureu amb el voltímetre la caiguda de tensió a les dues resistències (V_R1 i V_Z) i la caiguda de tensió total (V_{tot, exp}). Anoteu aquests valors en el full de pràctiques.

Tot seguit substituïu la resistència R per la bobina i mesureu la caiguda de tensió a la resistència (V_R1), a la bobina (V_Z), la caiguda de tensió total i la intensitat (V_{tot, exp}).

Repetiu les mesures posant ara el condensador en el lloc de la bobina.

Observareu que la suma de les tensions parcials (V_R1 + V_Z) només en un cas és igual a la de la tensió total ( V_{tot, exp}). Això és degut a la diferència de fase entre el voltatge aplicat i la intensitat que circula pel circuit quan no hi ha una resistència pura. En general, les expressions del voltatge i la intensitat seran:

a on  φ_v i φ_I  són les fases inicials de la tensió i la intensitat respectivament.

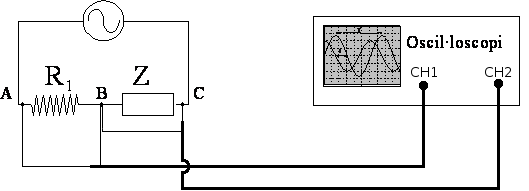
Per comprovar que existeix aquesta diferència de fase utilitzarem un oscil·loscopi. Incorporeu l’oscil·loscopi al muntatge tal com indica la figura 3.

Figura 3. Connecteu el canal 1 de l'oscil·loscopi entre A i B i el canal 2 entre C i B. Tingueu present que els endolls negres de les sondes (tots dos connectats a la massa de l'aparell) han d'anar situats al mateix punt, en aquest cas al punt de referència, B. En aquest muntatge la tensió VAB (tensió que cau a la resistència òhmica R1) permet de visualitzar la intensitat que circula pel circuit i, per tant, per Z. La tensió VCB permet de visualitzar directament la tensió que cau en l’element Z.

Poseu l’oscil·loscopi en mode base de temps de manera que vegeu tots dos canals alhora. Ara podreu calcular el desfasament entre els dos senyals, que serà el mateix que hi ha entre el voltatge i la intensitat. La diferència de fase entre dos senyals de la mateixa freqüència pot determinar-se si es visualitzen els dos senyals a la pantalla de l'oscil·loscopi i es mesuren el temps t i el període T que s'indiquen a la figura 4. Per mesurar-los podrà utilitzar els cursors de temps. Cal tenir present que, per la manera de connectar les sondes (amb els dos endolls negres al punt B del circuit), estareu introduint un desfasament de 180°, ja que estareu mesurant V_AB i V_CBen lloc de V_AB i V_BC. Aquest desfasament instrumental no pot corregir-se permutant els connectors d’una de les sondes (proveu de fer-ho i observeu-ne el resultat), i cal corregir-lo matemàticament invertint a l’oscil·loscopi el signe d’un dels dos senyals.

Per als tres casos considerats (en els que hem posat en el lloc de Z la resistència R, la bobina L i el condensador C) mesureu el desfasament entre la tensió i la intensitat amb la precisió més alta possible. Anoteu els resultats i dibuixeu en el full d’informe les figures que heu observat a l’oscil·loscopi. Identifiqueu clarament els senyals observats i poseu especial atenció en el signe del desfasament.

Les relacions entre el voltatge total mesurat en cada cas i la suma dels voltatges parcials, també por establir-se si tractem les magnituds sinusoïdals com a fasors. En aquest cas a cada magnitud depenent del temps se li associa un vector de mòdul la seva amplitud i amb un angle respecte a l’eix x que serà la seva fase inicial (figura 5).

Figura 5	Figura 6

Així representats, els fasors es poden sumar de la mateixa manera que es faria amb dos vectors. Per al cas de l’associació sèrie, atès que la intensitat és la mateixa per a tots els elements, representarem la intensitat en l’eix de les x i referirem a aquest eix les magnituds de les diferents tensions del circuit. Per al cas de dos elements, la tensió suma s’obtindrà gràficament com es mostra a la figura 6.

La tensió resultant es calcula aplicant la següent relació geomètrica:

Donat que coneixeu el mòdul i la fase de les tensions V_R1 i V_Z, feu la representació fasorial pels casos de la bobina i el condensador i calculeu el mòdul de la seva suma (V_{tot, calc}). Comproveu que, ara, aquest valor si que coincideix amb el valor mesurat de la tensió total (V_{tot, exp}).

11.3.2 Corba de ressonància

Connecteu el generador de funcions (sortida 50 Ω) en sèrie amb la resistència de 10 Ω,  la bobina i el condensador. A continuació connecteu el canal 1 de l’oscil·loscopi a la resistència, i el canal 2 a tot el conjunt RLC, tot parant esment a la correcta connexió del terra per a cada canal. Amb aquesta connexió la lectura del canal 1 correspondrà a la tensió a la resistència, que és proporcional a la intensitat del circuit, i la lectura del canal 2 correspondrà a la tensió al conjunt RLC. Ajusteu l’amplitud del generador de funcions a un valor proper al màxim.

Figura 7

Prement el botó AUTO-SET de l’oscil·loscopi podeu visualitzar els senyals dels dos canals. Seguidament, configureu els menús de l’opció MEASURE per mesurar simultàniament la freqüència del senyal, i la tensió RMS tant del canal 1 com del canal 2. Amb aquesta configuració podeu llegir ràpidament les tres magnituds que us interessa enregistrar per poder obtenir la corba de ressonància. Un cop realitzada aquesta operació, teniu el dispositiu preparat per poder procedir amb les mesures.

En primer lloc, centreu acuradament els dos senyals a la pantalla de l’oscil·loscopi, de manera que se superposin. Varieu la freqüència del generador fins que els senyals es trobin exactament en fase (al llarg del procés haureu d’anar ajustant la base de temps i la sensibilitat per tal de visualitzar-los correctament). En aquesta situació, la freqüència corresponent és la freqüència de ressonància. Anoteu les lectures d’aquesta freqüència i de les dues tensions. Observeu el canvi de signe de la fase a banda i banda de la freqüència de ressonància.

Un cop enregistrats els valors de la ressonància, ja podeu procedir a obtenir la resta de mesures. Fent servir la combinació AUTO-SET/MEASURE, enregistreu les lectures de la freqüència i de les tensions als dos canals per un espectre de freqüències entre 30 Hz i 100 kHz, a raó de dues per dècada convenientment espaiades. L’aparició d’un signe ? al costat d’una mesura indica que l’oscil·loscopi no l’està realitzant correctament, situació que es dóna principalment a les freqüències extremes. Aquest efecte es corregeix acabant d’ajustar manualment la sensibilitat del canal problemàtic o la base de temps.

A la vista dels valors obtinguts, acabeu de completar la col·lecció de mesures amb uns quants valors addicionals al voltant del pic de ressonància, la qual cosa us permetrà de representar-lo convenientment. Amb un total d’unes 15 mesures per a l’espectre complet (incloent-hi la de ressonància) és suficient per poder-ne fer una bona representació.

Substituïu la resistència de mesura per una de 100 Ω i repetiu el procediment i les mesures anteriors.

12.4 Realització de l’informe

En el Full de Laboratori:

1. Completeu la taula de l’apartat 11.3.1 per a la suma de tensions d’impedàncies connectades en sèrie.
2. Dibuixeu les figures observades a l’oscil·loscopi que mostren el desfasament entre la tensió i la intensitat en els tres casos considerats. Indiqueu el període T, la freqüència f, el temps t, i l’angle φ de desfasament que se’n dedueix.
3. Feu la representació fasorial corresponent a les associacions sèrie R-L i R-C.
4. Completeu la taula de l’apartat 11.3.2 i representeu en un mateix gràfic els punts experimentals corresponents a l’admitància del circuit RLC en funció de la freqüència per a les dues resistències estudiades.
5. A partir dels valors trobats per a la freqüència de ressonància calculeu el valor de LC corresponent i compareu-lo amb l’obtingut a partir dels resultats de l’apartat a).
6. A partir del pic de la ressonància, trobeu la resistència de la bobina.
7. (opcional) En el gràfic anterior, representeu en traç continu la dependència de l’admitància en funció de la freqüència calculada a partir dels valors de la resistència total, la inductància i la capacitat del circuit RLC. Compareu la dependència calculada amb l’obtinguda experimentalment.
8. Determineu l’amplada de banda i el factor de qualitat del circuit RLC en els dos casos analitzats.