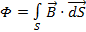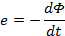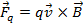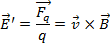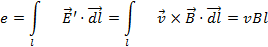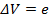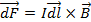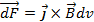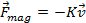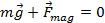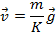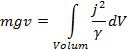8. INDUCCIÓ ELECTROMAGNÈTICA I CORRENTS DE FOUCAULT

Resum. La inducció electromagnètica és segurament l'aspecte de més transcendència tecnològica de l'electromagnetisme. En aquest estudi s'analitzaran aspectes com la força electromotriu induïda, els corrents induïts, i les forces sobre els circuits deguts a la inducció, parant atenció també al cas en que es produeixen els anomenats corrents de Foucault.

8.1 Fonaments

8.1.1 Inducció electromagnètica

El flux magnètic a través d'una superfície oberta (que té un camí tancat com a contorn) ve donat per

Els experiments mostren que quan el flux magnètic que travessa un circuit varia, en aquest s'indueix una força electromotriu donada per la Llei de Henry-Faraday

on el signe – que apareix en aquesta expressió expressa la Llei de Lenz.

8.1.2 Força electromotriu de moviment

Un dels motius que fa aparèixer forces electromotrius induïdes és el desplaçament de càrregues elèctriques en el si d'un de camp magnètic. L'origen del fenomen és la força magnètica que experimenta una càrrega, q, que es mou amb una velocitat, v, en un camp magnètic, B

Aquesta força equival a l'aparició d'un camp electromotor donat per

Per exemple, si una barra conductora recta, de longitud l, es mou en el si d'un camp magnètic uniforme, amb una velocitat v perpendicular al camp i a la barra, apareixerà una f.e.m. donada per

8.1.3 Corrents de Foucault

Si els camps electromotors es produeixen en un circuit obert no hi haurà corrents i sí que apareixeran diferències de potencial:

Si el circuit és tancat els camps electromotors donaran lloc a corrents elèctrics.

Una tercera possibilitat, molt més complexa, es dóna quan el conductor no és pròpiament un circuit elèctric. És el cas, per exemple, d'una peça conductora en forma de làmina plana. En aquestes geometries, la distribució de corrents és volúmica, amb una densitat  j, que és funció del punt i que dóna lloc a una distribució de corrent que sovint no és calculable analíticament.

Aquests corrents reben el nom de corrents de Foucault (eddy currents en terminologia anglosaxona) i són la base, entre altres aplicacions pràctiques, del funcionament de les cuines d'inducció.

8.1.4 Forces sobre els corrents induïts

Quan en els circuits es produeixen corrents induïts, apareixen les corresponents forces magnètiques

I, si es tracta de corrents de Foucault, un element de volum, dv, del conductor experimentarà una força

En qualsevol dels dos casos, el valor de la força total s'obtindrà per integració.

Quan s'analitza el problema amb més detall es demostra que l'esmentada força és proporcional a la velocitat i oposada al moviment, de forma anàloga al fregament viscós (de Stokes) que es produeix quan un sòlid es desplaça en un fluid:

on K és una constant que té en compte els elements particulars de l'experiment, bàsicament la geometria i la conductivitat del conductor que es desplaça.

8.1.5 Velocitat de caiguda constant

En el cas particular que s'estudiarà en el laboratori, les forces que actuen són la de la gravetat, que tendeix a accelerar la làmina cap avall, i la força magnètica que està dirigida cap amunt, ja que s'oposa al moviment de caiguda. En el règim permanent, que s'assoleix molt ràpidament, la resultant d'aquestes dues forces és nul·la

i, consegüentment, la velocitat és constant. Per a una determinada geometria, donada pel valor de K, les dues expressions anteriors proporcionen

8.1.6 Energia

La conservació de l'energia comporta que la potència que desenvolupa la força de la gravetat es dissipa per efecte Joule en els corrents d'inducció, que si es tracta de corrents de Foucault, val

8.1.7 Objectius de l'estudi

En aquest estudi es desenvoluparan els següents experiments:

1. Generació de corrents d'inducció en una bobina.
2. Obtenció de la Llei de Lenz.
3. Corrents de Foucault en un bloc conductor i velocitat de caiguda constant.
4. Proporcionalitat entre la força deguda a la inducció electromagnètica i la velocitat.
5. Força electromotriu induïda en un fil conductor desplaçant-se a velocitat constant.
6. Força electromotriu induïda en una espira desplaçant-se a velocitat constant.
7. Diferències de potencial degudes als corrents de Foucault.

8.2 Dispositiu experimental

Per als estudis (a) i (b):

• solenoide que porta indicat esquemàticament com s'ha fet el bobinat, és a dir, quina és la correlació entre el sentit de gir del corrent en les espires del solenoide i els seus terminals de connexió.
• galvanòmetre analògic de dos sentits de mesura. Si el corrent hi entra pel terminal positiu (cable vermell) l'indicador assenyala positiu (cap a la dreta).
• imant muntat sobre un suport que mostra esquemàticament les línies del camp magnètic.

Per als estudis (c), (d), (e), (f) i (g):

• làmina d'alumini de 1 mm de gruix i de 43 g.
• làmina d'alumini de 6 mm de gruix, que incorpora un fil conductor transversal i una espira rectangular. Molt important: cap d'aquests endolls s'ha de connectar mai a la xarxa elèctrica.
• làmina d'alumini de 6 mm de gruix, que incorpora dos contactes elèctrics per a la mesura de la diferència de potencial deguda a l'aparició de corrents de Foucault. Molt important: cap d'aquests endolls s'ha de connectar mai a la xarxa elèctrica.
• làmina de PVC de 3 mm de gruix.
• multímetre HP 34401A, que permet l'enregistrament seqüencial en memòria de tot un seguit de mesures de tensió.
• cronòmetre.
• blocs d'alumini de 20,4 g i de 40,7 g que s'utilitzaran com a llast.
• bloc d'espuma per a evitar cops.
• un sistema d'imants, fixat a la part superior de la taula de treball, que aplica un camp magnètic horitzontal de 0,77 T en una regió de 5 cm d'alçada. Avís important: Queda totalment prohibit acostar a la zona de camp magnètic cap objecte que no sigui les làmines que s'utilitzen en els estudis.

8.3 Procediment experimental

8.3.1 Corrents d'inducció

1. Primera observació: Alineeu coaxialment l'imant i el solenoide, i acosteu el primer al segon. Observeu que el galvanòmetre detecta l'aparició de corrent elèctric en el circuit.
2. Efecte del mòdul de la velocitat: Repetiu l'apartat (a) a una velocitat més lenta i una més ràpida i anoteu quin efecte té això en com és de gran la intensitat de corrent. Anoteu quina relació hi ha entre els sentits del corrent elèctric obtinguts en un cas i en l'altre. Anoteu també què és el que passa quan deixeu quiet l'imant (v = 0)
3. Efecte del sentit del camp magnètic: Repetiu l'apartat (a) havent invertit l'eix de l'imant. Anoteu quina relació hi ha entre els sentits del corrent elèctric obtinguts en un cas i en l'altre.
4. Efecte del sentit de la velocitat: Repetiu l'apartat (a) primer acostant i després allunyant l'imant del solenoide. Anoteu quina relació hi ha entre els sentits del corrent elèctric obtinguts en un cas i en l'altre.
5. Efecte de l'orientació espacial del camp magnètic aplicat: Repetiu l'apartat a) però havent alineat perpendicularment l'imant a l'eix del solenoide. Compareu qualitativament la magnitud del corrent en relació al obtingut a (a).
6. Velocitat relativa: Repetiu l'apartat (a) deixant quiet l'imant i acostant el circuit. Anoteu si, per velocitats relatives semblants, s'observa cap diferència respecte de l'apartat (a).

8.3.2 Obtenció de la Llei de Lenz

En alguns dels experiments de l'estudi anterior s'ha observat un canvi de sentit del corrent induït en relació a l'observat a l'apartat (a), però encara no s'ha justificat el perquè del sentit en un experiment individual. Per tal de fer-ho, tingueu present que:

1. Un corrent circulant per un circuit crea camp magnètic i això fa que el propi circuit estigui travessat per un flux magnètic degut al propi corrent.
2. Per a un determinat corrent, el camp magnètic queda unívocament determinat en tots els punts de l'espai.
3. El corrent i el flux que crea en el propi circuit, són escalars que sempre tenen el mateix signe, que, per convenció, queda determinat quan, arbitràriament, triem com a positiu un dels dos possibles sentits de circulació del circuit. En efecte, si triem com a positiu el sentit amb el que realment circula la intensitat (I és positiva), el sentit del camp magnètic B, creat pel corrent, és el mateix que els vectors dS (vegeu figura 1), i en resulta un flux positiu. Si, en canvi, triem com a positiu el sentit contrari a la intensitat (I és negativa), el sentit de dS és contrari a B i en resulta un flux negatiu.

Tenint present tot això, repetiu l'experiment (a) de l'estudi 8.3.1, prenent nota de:

1. Quin és el sentit de circulació en el solenoide que considerareu positiu.
2. Quina és la direcció i sentit que ha de tenir un camp vectorial que, a partir del que s'ha fixat al punt anterior, doni lloc a un flux positiu sobre el solenoide.
3. Com a conseqüència del criteri fixat al punt anterior, quin és el signe del flux magnètic que apliquem amb l'imant, Φ_aplicat.
4. Quin moviment s'aplica a l'imant: acostar-lo al solenoide implica augmentar el mòdul de B, mentre que allunyar-lo implica disminuir el mòdul de B.
5. Quin signe té la variació de flux magnètic aplicat, degut a l'acció del punt anterior, ΔΦ. Aquest signe dependrà del signe del flux i de si el mòdul de B ha augmentat o ha disminuït.
6. Quin és el signe del flux creat pel corrent induït (que, tal com s'ha dit, és igual al del corrent que s'ha induït) Φ_induït.
7. Repetiu els punts anteriors, combinant diferents alternatives en els paràmetres de l'experiment. Ompliu la taula de l'informe amb els resultats de tres experiments d'aquest tipus, anotant per cadascun d'ells:

• Quin és el pol de l'imant que heu encarat a l'espira (N o S).
• Quin és el sentit positiu, per exemple mirant des de l'imant, de recórrer l'espira (horari o antihorari).
• Quin és el signe (+ o -) del flux magnètic aplicat inicialment, que haurà quedat determinat per allò que heu triat en els dos punts anteriors.
• Quina és la variació de la posició relativa (acostem l'imant a l'espira o l'allunyem).
• Quin és el signe del corrent i del flux magnètic induït (+ o -).
• Què és el que sempre s'observa, quan es contrasten els resultats?

8. Prengueu les dades que calguin per a poder dibuixar esquemàticament els elements rellevants i el resultat en un dels casos estudiats.

8.3.3 Aparició de forces degudes als corrents de Foucault quan un bloc conductor es desplaça en el si d'un camp magnètic

Situeu la làmina d'alumini prima dins de la cavitat amb camp magnètic (entrant-la per sota, tal com mostra la figura 2), i deixeu-la caure (havent posat sobre la taula l'espuma per a evitar els cops). Descriviu la forma (amb velocitat uniforme o acceleradament) en que va caient. Compareu-ho amb el que succeeix quan deixeu caure una làmina de PVC (aïllant elèctric) i amb una làmina conductora d'alumini, més gruixuda.

8.3.4 Velocitat de caiguda uniforme.

Repetiu l'experiment de deixar caure la làmina mesurant quina és la seva velocitat, v₀, mitjançant un cronòmetre i les marques de la làmina i del suport/guia. Per fer-ho mesureu el temps que, en caure, tarda en recórrer 5, 10, 15, 20 i 25 cm.

8.3.5 Força magnètica proporcional a la velocitat

Aquesta proporcionalitat s'estudiarà afegint diferents llasts a la làmina i mesurant la corresponent velocitat de caiguda. En afegir més massa, i un cop assolida una velocitat constant de caiguda, la força deguda als corrents d'inducció també és més gran.

Afegiu una massa Δm₁ = 20,4 g a la làmina prima d'alumini. Repetiu el procediment de deixar-la caure i mesurar la velocitat de caiguda (solament caldrà fer-ho per al recorregut de 25 cm). Repetiu el procediment per a  Δm₁ = 40,7 g i per a  Δm₁ = (20,4 + 40,7) g

8.3.6 Preparació del voltímetre i el PC per a l'enregistrament de mesures V(t)

En els apartats 8.3.7, 8.3.8 i 8.3.9 s'enregistraran mesures V(t), per a la qual cosa cal, prèviament, engegar el voltímetre i el PC i procedir tal com s'indica a continuació:

1. Obriu el full Excel Adquisició que es troba a l'escriptori de l'ordinador. Per tal de poder capturar lectures del voltímetre caldrà que accepteu l'execució de Macros i contingut ActiveX.

2. Cliqueu sobre el botó Get UserForm per tal d'obrir l'eina d'adquisició de dades dels experiments descrits als apartats 8.3.7, 8.3.8 i 8.3.9.. Una vegada oberta, assegureu-vos que a la finestra Address figuri GPIB::22. En cas contrari, aviseu al professor.

3. Seleccioneu la Funció DC Volts en el panell de selecció Function.

4. Una vegada tingueu l'experiment preparat, cliqueu sobre els botons Fil, Espira o Foucault per tal d'iniciar una adquisició de punts amb el voltímetre durant 5 segons. El voltímetre emet un so d'avís abans d'iniciar l'adquisició. Cada botó col·loca els valors de tensió enregistrats en una columna diferent (Fil:columna B, Espira:columna C, Foucault:columna D).

5. Guardar el fitxer. El fitxer Adquisició no es pot guardar amb les modificacions. Un cop efectuats els experiments, les dades enregistrades poden copiar-se en un nou full de càlcul o guardar-se amb un nou nom amb l'opció “Guardar como...”. 

8.3.7 Força electromotriu en un fil conductor

En aquest experiment es mesurarà la diferència de potencial en terminals del fil conductor quan aquest es mou perpendicularment a un camp magnètic. El fil conductor està muntat en una làmina d'alumini que solament juga el paper de suport mecànic i el de garantir que la velocitat de caiguda sigui constant i prou lenta. Connecteu el fil al multímetre, prepareu el voltímetre i el PC per a l'enregistrament segons s'ha indicat a 8.3.6, i introduïu la làmina a la zona de camp magnètic tal com s'ha fet a 8.3.3. Premeu el botó d'adquisició Fil i, després de sentir el so d'avís del voltímetre, deixeu caure la làmina. Els valors quedaran enregistrats en la columna B del full de càlcul.

8.3.8 Força electromotriu en una espira conductora

 Repetiu 8.3.7 connectant al multímetre l'espira rectangular i utilitzant el botó Espira per a fer l'adquisició. Els valors quedaran enregistrats en la columna C del full de càlcul.

8.3.9 Diferències de potencial degudes als corrents de Foucault

 Repetiu 8.3.7 connectant al multímetre la làmina d'alumini que incorpora dos contactes elèctrics sobre la pròpia làmina i utilitzant el botó Foucault. Els valors quedaran enregistrats en la columna D del full de càlcul.

8.4 Elaboració de l'informe

1. A partir dels resultats obtinguts a 8.3.2, presenteu la taula que allí s'indica. Dibuixeu esquemàticament la geometria i els paràmetres en un dels cassos de la taula.
2. A partir dels resultats obtinguts a 8.3.4, presenteu la gràfica del temps de caiguda en funció de la distància recorreguda. Obteniu, per regressió lineal, el valor de la velocitat.
3. A partir dels resultats obtinguts a 8.3.5, presenteu la gràfica de la velocitat en funció de la força magnètica.
4. Representeu, en una sola gràfica, les dependències de la tensió amb el temps enregistrades en els apartats 8.3.7, 8.3.8 i 8.3.9. Comenteu els aspectes que considereu rellevants de la gràfica.
5. Feu un resum de tot l'estudi efectuat i poseu-lo, a mode d'abstract, al principi de l'informe, després del títol i els autors.