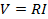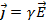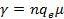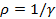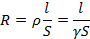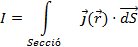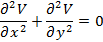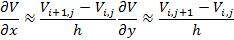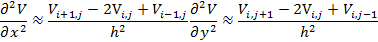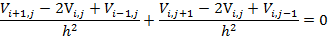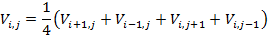4. CONDUCTIVITAT ELÈCTRICA

Resum. La Llei d’Ohm estableix la proporcionalitat, observada experimentalment en molts materials conductors, entre el corrent i el camp elèctric. En aquesta pràctica se l'estudiarà des del punt de vista de les magnituds integrals (V i I) i puntuals (E i j), parant atenció en els aspectes geomètrics (elèctrodes, discontinuïtats de camp i de corrent..). Per a aquest segon estudi es mesurarà el valor del potencial en els diferents punts d'una làmina resistiva i, a partir d'aquestes dades, es farà una estimació del camp elèctric, la densitat de corrent i la conductivitat. Finalment s'obtindrà una modelització del mateix problema basada en la resolució numèrica de l'equació de Laplace, que es compararà amb les mesures.

4.1 Fonament

4.1.1 Llei d'Ohm i conductivitat elèctrica

Una resistència és un element de circuit, de tipus passiu, on la diferència de potencial, V, és proporcional al corrent, I, que hi circula

i on la constant de proporcionalitat, R, s'anomena resistència i es mesura en ohms. Aquesta proporcionalitat entre magnituds integrals és conseqüència de la proporcionalitat que hi ha, a nivell de cada punt del medi, entre el camp elèctric aplicat i la densitat de corrent que s'hi estableix

 on γ s'anomena conductivitat del material i depèn de la densitat volúmica, n, de partícules mòbils amb càrrega elèctrica (conegudes com a portadors de càrrega), del valor de la seva càrrega (normalment la de l'electró, q_e), i de la seva mobilitat, μ. 

En els estudis sovint també s'utilitza l'anomenada resistivitat

Si la geometria de la resistència és de tipus fil, de secció constant S i longitud l, la resistència i la conductivitat estan relacionats per

A diferència de la resistència, que és una propietat d'un element de circuit i depèn de la naturalesa del conductor i de la geometria, la conductivitat elèctrica és una propietat de cadascun dels punts del conductor. Des del punt de vista experimental podem mesurar fàcilment el valor d'una resistència però per a la mesura de la conductivitat cal tenir informació de la homogeneïtat del conductor i de la seva geometria.

4.1.2 Bloc resistiu i elèctrodes

En  una resistència distingim dos elements importants:

El bloc de material resistiu, que presenta una certa forma geomètrica i que ve limitat per unes superfícies finals

Uns contactes elèctrics (normalment dos) anomenats elèctrodes. La seva baixa resistivitat i geometria determina que cadascun d'ells és una regió equipotencial, de forma anàloga al que succeeix amb els conductors en electrostàtica.

En els punts de la resta del sistema, que normalment són no conductors (γ = 0), pot haver-hi camp elèctric aplicat, però no s'hi estableix cap corrent

4.1.3 Línies de corrent

Quan entre els dos elèctrodes s'aplica una diferència de potencial estacionari, s'estableix:

• un cert valor de la funció potencial V(r) en tots els punts de l'espai. Sovint es visualitza V(r) mitjançant les anomenades superfícies equipotencials.
• un cert camp elèctric (de tipus electrostàtic, E(r) = - grad V) en tots els punts de l'espai. Sovint es visualitza E(r) mitjançant les anomenades línies de camp que, en cada punt, són perpendiculars a les superfícies equipotencials.
• unes densitats de càrrega elèctrica, en els elèctrodes i en les superfícies de discontinuïtat, que són les que determinen la distribució final de potencial .
• unes densitats de corrent j(r) en els punts del bloc resistiu, que si es tracta d'un medi òhmic i en virtut de (2), són proporcionals al camp E. A partir de j(r), s'acostuma a dibuixar les anomenades “línies de corrent”, de forma anàloga a les línies de camp elèctric, dibuixades a partir de E(r).

• un corrent, I, que és el flux de j(r) a través d'una secció transversal qualsevol (que deixi un elèctrode a cada costat) del bloc resistiu.

4.1.4 Equació de Laplace

Es pot provar que si el medi és ohmic i homogeni, l'equació diferencial que determina V(r) és l'equació de Laplace, ΔV = 0. La mateixa, i amb la mateixa solució, que resultaria si es plantegés el problema d'electrostàtica amb les mateixes condicions de contorn (valors del potencial i/o de les càrregues elèctriques en les superfícies límit de la regió estudiada). És a dir, si substituïm el medi resistiu per un medi aïllant, mantenint totes les càrregues distribuïdes a l'espai, la V(r) seria la mateixa que si el medi és resistiu.

4.1.5 Geometria plana

Els elements establerts a l'apartat 4.1.3 es poden estudiar molt directament si la resistència és de geometria plana. En aquest cas, les equipotencials no seran superfícies, sinó línies.

4.1.6 Solució numèrica de l’equació de Laplace

L’equació de Laplace és una equació diferencial en derivades parcials que ha de satisfer el potencial elèctric en les regions lliures de càrrega neta. En dues dimensions l’equació de Laplace s’escriu com:

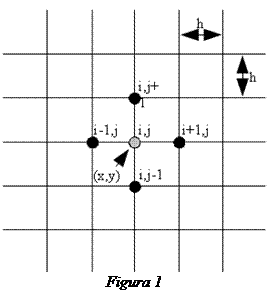
Aquesta equació pot resoldre’s numèricament tot utilitzant el mètode anomenat de relaxació.  Discretitzem el pla x,y de manera que formi una malla bidimensional com es mostra a la figura 1, on les coordenades x,y han estat substituïdes pels índexs i,j. Les derivades primera i segona del potencial les podem aproximar per:

on h és la mida de la cel·la unitària de la discretització. Substituint a l’equació (7) queda: 

si resolem aquesta equació tenim:

aquesta expressió indica que si la funció V(x,y) satisfà l’equació de Laplace en dues dimensions, el valor del potencial V(i,j) en un punt del pla (i,j) és igual a la mitjana del valor del potencial en els quatre punts veïns més pròxims. Fent ús d’aquesta propietat resoldrem l’equació de Laplace en un full de càlcul fent que el valor d’una cel·la donada sigui el valor de la mitjana de les seves veïnes més pròximes, exceptuant les cel·les dels elèctrodes que tenen un potencial fix. Seguidament farem iteracions necessàries fins que el valor de les cel·les no canviï o bé que canviï en una quantitat més petita d’un valor prefixat (per exemple un 0,1%). 

4.2 Dispositiu experimental

• 1 font de tensió variable
• 1 amperímetre
• 1 voltímetre amb connexió a l'ordinador mitjançant bus RS-232
• diferents mostres resistives (marcades amb 1 i 2), amb geometria plana, preparades per a la mesura de la distribució de potencial, on s'han establert els corresponents elèctrodes. 0.03 mm de gruix.
• Ordinador amb impressora
• Full de càlcul Excel per l’adquisició de dades experimentals (potencials).

4.3 Procediment experimental

4.3.1 Mesura de la resistència

Connecteu una de les làmines resistives segons l'esquema a)

Varieu la tensió, V, que la font aplica a la làmina resistiva (des de 0 a 10 V) i llegiu, per a cada V, la corresponent intensitat, I, que circula per la làmina. Obteniu uns 10 valors regularment espaiats. En acabar, reduïu la tensió de la font a zero, canvieu el sentit del corrent del circuit (permutant els connectors de la font), i repetiu l'adquisició I(V) que heu fet per a intensitats positives.

Repetiu el procediment de l'apartat anterior per a la segona làmina resistiva.

4.3.2 Mesura de la distribució de potencial

Munteu el circuit de l'esquema b) amb la làmina resistiva 1. El multímetre que utilitzareu com a voltímetre és el que està connectat a l'ordinador (amb un terminal connectat a la font i l'altre a l’elèctrode de mesura, que acaba amb una bola per a evitar danyar el paper conductor). Feu que la font proporcioni ΔV=5V, i comproveu tocant amb l’elèctrode de mesura (acabat amb una bola) que els elèctrodes a la làmina tinguin els potencials: 0 V i 5 V.

Seguidament, amb el sistema d’adquisició de dades de l’ordinador, mesureu i enregistreu els potencials dels punts de la malla marcada sobre el full conductor. Engegueu l’ordinador i obriu l’arxiu Adquisició3 (llibre Excel) que apareix en el centre de l’escriptori. Deseu l’arxiu amb l’opció “Guardar como” a la carpeta del vostre grup i trieu un nom per a l’arxiu (aquest serà l’arxiu amb el que treballareu). Seleccioneu el primer full del llibre (Adquisició) per tal de visualitzar a la pantalla de l’ordinador la malla i els elèctrodes. Per fer la mesura d’una cel·la heu de seleccionar-la amb el ratolí, posar l’elèctrode de mesura (bola) sobre el punt del paper en qüestió i prémer amb el ratolí el botó que apareix a la part inferior de la pantalla. A causa de la simetria dels elèctrodes en el full conductor només heu de mesurar la meitat superior de les cel·les, des de la (0,10) fons a la (28,20). Observeu a la pantalla com es distribueixen els valors dels potencials i les equipotencials amb diferent color.

Quan hagueu mesurat el potencial de totes les cel·les premeu el botó “Equipotencials”. Apareixerà una nova finestra on el programa corresponent us permet de seleccionar quin voleu que sigui l'increment de potencial entre dues línies equipotencials consecutives (Div). Per tal que es generi el diagrama de línies equipotencials cal que premeu el botó "Marxa". Imprimiu el diagrama obtingut seguint el protocol penjat a la taula..

Repetiu la mesura amb la làmina resistiva 2.

4.3.3 Càlcul numèric de la distribució de potencial

Seleccioneu el segon full del llibre Excel (Simulació). Apareixerà la malla bidimensional amb el valor de totes les cel·les a zero. Abans de començar a calcular cal fixar el valor del potencial dels elèctrodes. Es simularà la configuració d'elèctrodes de la làmina 2. Per fer-ho, dibuixeu la configuració del elèctrode amb potencial negatiu seleccionant les cel·les corresponents amb el ratolí mentre manteniu pressionada la tecla 'Control' dreta del teclat. Una vegada seleccionades, premeu el botó “Elèctrode1” per a assignar el potencial negatiu a totes elles. Repetiu el procès per a l'elèctrode amb potencial positiu assignant-li el valor amb el botó “Elèctrode2”.

Ara ja podeu començar a iterar amb la rutina de resolució de la Laplaciana implementada en el full de càlcul. Per fer-ho, entreu en la cel·la 7AK un nombre d’iteracions petit (per exemple 10) i premeu el botó “Marxa”. En repetir aquest procediment observareu a la pantalla com, cada vegada que iterem, la distribució de potencials calculada es va assemblant a l’experimental mesurada abans. Per tal de fer les iteracions d’un sol cop entreu un nombre d’iteracions elevat (per exemple 1000). Un cop acabat, premeu el botó equipotencials i procediu com en l’apartat anterior per visualitzar les equipotencials i per imprimir el resultat final.

4.4 Realització de l’informe

4.4.1 Mesura de resistències.

De 4.3.1, representeu en una mateixa gràfica I(V) les dades obtingudes per a les làmines conductores mesurades. Feu l'ajust lineal i determineu el valor de la resistència en cada cas. Justifiqueu perquè les dues mostres presenten diferent resistència.

4.4.2 Superfícies equipotencials, línies de camp i línies de corrent

De les dades obtingudes a 4.3.2, imprimiu les línies equipotencials de la distribució mesurada. Al gràfic obtingut per a la làmina 1 afegiu-hi, dibuixades a mà, les línies de camp elèctric, vigilant que:
• surtin de l'elèctrode de més potencial i vagin a parar al de menys (poseu una fletxa que indiqui el sentit de la línia).
• que en aquells punts on les superfícies equipotencials estiguin més juntes (el camp elèctric és més intens) cal que les línies de camp que dibuixeu també estiguin més juntes.
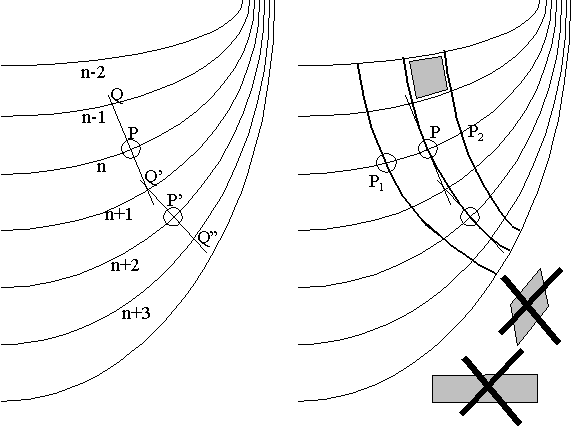
Per tal de fer-ho amb bon criteri, seguiu el següent procediment (vegeu figura):
• Trieu un punt, P, qualsevol d'una superfície equipotencial (la n-èssima) que estigui situat aproximadament al centre del gràfic. Per aquest punt hi passarà la primera línia de camp.
• Dibuixeu un segment que, en aquest punt, sigui perpendicular a la superfície equipotencial i allargue-lo fins que talli les dues superfícies equipotencials veïnes (punts Q i Q').
• Sobre la superfície equipotencial n+2, busqueu per quin punt ha de passar una perpendicular a aquesta superfície equipotencial per a que talli a n+1 en el punt Q'.
• Dibuixeu un segment que, en aquest punt, sigui perpendicular a la superfície equipotencial i allargue-lo fins que talli la següent superfície equipotencial (punt Q'').
• Repetiu els processos descrits fins que aneu d'un elèctrode (0 V) a l'altre (5 V).
• Uniu els punts P(i) amb una línia (que en general serà corba) que anirà d'un elèctrode a l'altre.
• La següent línia dibuixeu-la de forma semblant a partir d'un punt P1 que estigui a una distància de P semblant a la distància que hi ha entre P i Q (les línies de camp han d'estar més juntes on les superfícies equipotencials també ho estan).
• Repetiu el procés fins a completar el diagrama de les línies de camp. Observeu que dues equipotencials i dues línies de camp determinen polígons de forma, aproximadament, quadrada (no han d'haver-hi ni “rectangles” ni “rombes”).

Sobre els diagrames de línies de camp, marqueu, amb un color diferent, quines de les línies de camp són, també, línies de corrent, i quines no.

4.4.3 Càlcul aproximat del camp elèctric

Estudiant el diagrama obtingut, es pot determinar aproximadament el valor del camp elèctric en un punt qualsevol, tot aplicant

(12)

on ΔV és la diferència de potencial entre les dues equipotencials properes al punt i Δx és la mínima distància que hi ha entre aquestes equipotencials (mesurada perpendicularment a elles). Presenteu els valors del camp en un punt on aquest sigui intens (E_intens) i en un altre on sigui feble (E_feble).

4.4.4 Càlcul aproximat de la densitat de corrent i de la conductivitat

Estudiant el diagrama obtingut, es pot determinar aproximadament el valor de la densitat de corrent en un punt qualsevol. Per fer-ho, determinem la quantitat de corrent que correspon a una línia de corrent, ΔI, que no és més que el corrent total (la diferència de potencial aplicada entre elèctrodes dividida per la resistència entre elèctrodes) dividit pel nombre, N, de tubs de corrent (apartat 4.4.2)

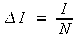(13)

La densitat de corrent es calcula dividint ΔI per la secció recta, ΔS, que travessa aquest corrent i que és igual al producte del gruix de la làmina conductora, d, per la distància que, en aquell punt hi ha entre línies de corrent, Δy.

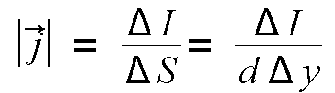(14)

Presenteu els valors de la densitat de corrent (j_intens i j_feble) en els mateixos punts on heu determinat els camps en l'apartat anterior.

En els dos punts on heu calculat el camp i la densitat de corrent, calculeu la conductivitat del paper conductor mitjançant

(15)

4.4.5 Superfícies equipotencials a partir de l'equació de Laplace

De 4.3.3, imprimiu les línies equipotencials de la distribució calculada i compareu la distribució obtinguda numèricament amb la mesurada.