| |
2.3 Propagación,
reflexión y refracción
Subsecciones
2.3.1 Deducción de
las leyes de la Óptica Geométrica
Una onda incide sobre una superficie que
separa dos medios dieléctricos
isótropos de índices  y y
 (véase la figura 2.7). Al interaccionar
con la superficie de separación,
parte de la energía vuelve al primer medio y parte se transmite al
segundo medio. Puesto que en la superficie de separación se verifican
las condiciones de contorno 2.4 y, en el caso
particular que estamos considerando la densidad superficial de carga y
las
corrientes superficiales son nulas, podemos escribir la continuidad de
las componentes del campo: (véase la figura 2.7). Al interaccionar
con la superficie de separación,
parte de la energía vuelve al primer medio y parte se transmite al
segundo medio. Puesto que en la superficie de separación se verifican
las condiciones de contorno 2.4 y, en el caso
particular que estamos considerando la densidad superficial de carga y
las
corrientes superficiales son nulas, podemos escribir la continuidad de
las componentes del campo:
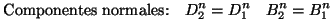 |
(2.33) |
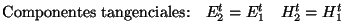 . . |
(2.34) |
Si tomamos, por ejemplo, la continuidad de la componente tangencial  de los campos eléctricos en la
superficie
de separación de medios (que por comodidad tomaremos en de los campos eléctricos en la
superficie
de separación de medios (que por comodidad tomaremos en ), podremos escribir: ), podremos escribir: 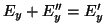 ,
Desarrollando
esta expresión tenemos ,
Desarrollando
esta expresión tenemos
 , , |
(2.35) |
donde  , ,  y y  son las amplitudes
tangenciales de los campos incidente, transmitido y reflejado y
son las amplitudes
tangenciales de los campos incidente, transmitido y reflejado y 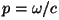 , , 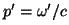 y y  . El punto considerado . El punto considerado  es un punto de la superficie
de
separación de los medios. Los vectores que indican la dirección
de propagación de la fase son es un punto de la superficie
de
separación de los medios. Los vectores que indican la dirección
de propagación de la fase son  , , 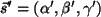 , ,
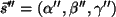 . .
Figura 2.7:
Deducción
de las leyes de la reflexión y de la refracción
|
|
La expresión de continuidad se debe verificar
en cualquier momento
y para cualquier punto. Por lo tanto, no puede depender de las
variables
espaciales o temporales. La única manera de que las variables no estén
presentes en la ecuación es que las tres fases sean iguales y, por
lo tanto, se puedan cancelar. Esto pasa si se verifica:
 : la
frecuencia no cambia al cambiar de medio la onda, ni al producirse
una reflexión. Sin embargo, dado que la velocidad de la luz
es dependiente del medio, la longitud de onda cambia, al cambiar de
medio. La longitud de onda de un campo propagándose en un medio
de índice : la
frecuencia no cambia al cambiar de medio la onda, ni al producirse
una reflexión. Sin embargo, dado que la velocidad de la luz
es dependiente del medio, la longitud de onda cambia, al cambiar de
medio. La longitud de onda de un campo propagándose en un medio
de índice  se relaciona
con la longitud de onda en el vacío ( se relaciona
con la longitud de onda en el vacío (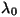 ), mediante la relación ), mediante la relación 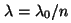 . . -
 :
Si se hace una rotación de ejes de manera que :
Si se hace una rotación de ejes de manera que 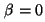 , esto implica necesariamente que , esto implica necesariamente que  , con lo que se prueba que el
rayo incidente, el reflejado y el transmitido están en el mismo plano. , con lo que se prueba que el
rayo incidente, el reflejado y el transmitido están en el mismo plano.
-
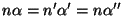 :
como la luz que se refleja vuelve al primero medio, obtenemos que :
como la luz que se refleja vuelve al primero medio, obtenemos que  . Proyectando
esta componente sobre el eje . Proyectando
esta componente sobre el eje  ,
tenemos que ,
tenemos que 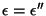 (ley de
la reflexión). Por otra parte, como se verifica que (ley de
la reflexión). Por otra parte, como se verifica que  , entonces
tenemos , entonces
tenemos 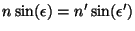 (ley de la refracción). (ley de la refracción).
2.3.2 Fórmulas de Fresnel
En esta sección estudiaremos los valores que
toma la amplitud del campo
al cambiar de medio o reflejarse, en función de la amplitud incidente.
Sea un frente de onda que avanza según la dirección . Consideremos un campo eléctrico
polarizado linealmente, que vibra en el plano definido por el frente de
onda.
Para hacer que el planteamiento del problema sea más claro,
proyectaremos
el vector campo eléctrico sobre dos ejes: un eje en el plano . Consideremos un campo eléctrico
polarizado linealmente, que vibra en el plano definido por el frente de
onda.
Para hacer que el planteamiento del problema sea más claro,
proyectaremos
el vector campo eléctrico sobre dos ejes: un eje en el plano 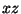 (eje paralelo) y un eje perpendicular
al anterior, que es paralelo al eje (eje paralelo) y un eje perpendicular
al anterior, que es paralelo al eje  (eje
perpendicular) y analizaremos cada caso por separado. El plano (eje
perpendicular) y analizaremos cada caso por separado. El plano 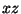 es el plano de incidencia. es el plano de incidencia.
2.3.2.1 Campo E
paralelo al plano de incidencia

Figura 2.8:
Fórmulas de
Fresnel. Campo E paralelo al plano de incidencia
![\includegraphics[width=10cm]{fres2db.eps}](img304.gif) |
Consideremos el primero caso, indicado en la
figura 2.8.
Tomemos la proyección del campo
eléctrico sobre el plano 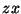 .
La dirección del campo magnético queda definida por la relación .
La dirección del campo magnético queda definida por la relación
 .
Puesto que no hay otros campos presentes en el problema que puedan
modificar
la dirección de los campos, las direcciones de éstos son las
que se muestran en la figura 2.8. El sentido
del campo eléctrico es tal que la componente .
Puesto que no hay otros campos presentes en el problema que puedan
modificar
la dirección de los campos, las direcciones de éstos son las
que se muestran en la figura 2.8. El sentido
del campo eléctrico es tal que la componente  sea positiva. Los campos se escriben de la manera
siguiente sea positiva. Los campos se escriben de la manera
siguiente
|
|
(2.36) |
|
|
 . |
Para simplificar la nomenclatura escribiremos los módulos de la
siguiente
manera  , , 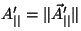 y y  . Para
deducir la relación entre las amplitudes, operaremos de la manera
siguiente: . Para
deducir la relación entre las amplitudes, operaremos de la manera
siguiente:
- Se proyecta la componente tangencial
 del campo eléctrico y se aplica la condición
de continuidad. del campo eléctrico y se aplica la condición
de continuidad.
- Se proyecta la componente tangencial
 del campo magnético y se aplica la condición
de continuidad. del campo magnético y se aplica la condición
de continuidad.
- Se escribe el campo magnético en términos del campo
eléctrico. De esta manera se obtiene un sistema de ecuaciones lineal
con dos incógnitas (
 y y  ), la solución del
cual es ), la solución del
cual es
 |
(2.37) |
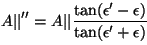 . . |
(2.38) |
2.3.2.2 Campo E
perpendicular al plano de incidencia

El segundo caso a considerar es análogo al
anterior, pero ahora el
campo eléctrico es perpendicular al plano 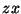 , según se indica en la figura 2.9. El campo
eléctrico se ha tomado
en el sentido positivo del eje , según se indica en la figura 2.9. El campo
eléctrico se ha tomado
en el sentido positivo del eje  .
Operando
de la misma forma que en el caso anterior, se obtiene la relación
entre la amplitud de los campos eléctricos transmitido y reflejado
en función del incidente, para el caso de polarización perpendicular. .
Operando
de la misma forma que en el caso anterior, se obtiene la relación
entre la amplitud de los campos eléctricos transmitido y reflejado
en función del incidente, para el caso de polarización perpendicular.
Figura 2.9:
Fórmulas de
Fresnel. Campo E perpendicular al
plano
de incidencia
|
|
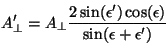 |
(2.39) |
 . . |
(2.40) |
Las ecuaciones 2.37-2.40 reciben el nombre
de Fórmulas de Fresnel.
Habitualmente se trabaja con los coeficientes de reflexión y
transmisión,
que se definen
|
|
(2.41) |
 . |
2.3.3 Análisis de
los coeficientes de transmisión y reflexión
A continuación se muestra la variación de los
cuatro coeficientes
de Fresnel en función del ángulo de incidencia  . Algunos casos de particular interés
son: . Algunos casos de particular interés
son:
- Incidencia normal (
 ): ):
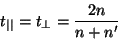 |
(2.42) |
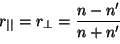 . . |
(2.43) |
- Ángulo de Brewster. Tenemos incidencia con ángulo de
Brewster cuando
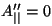 . En este
caso, la componente reflejada presenta exclusivamente polarización
perpendicular. Esto pasa cuando . En este
caso, la componente reflejada presenta exclusivamente polarización
perpendicular. Esto pasa cuando
 . . |
(2.44) |
- Ángulo límite: ángulo de incidencia para el que
 : :
 . . |
(2.45) |
Este ángulo sólo tiene sentido cuando 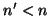 . .
Cuestiones interesantes que podemos extraer
del análisis de las figuras:
- En incidencia normal y para valores pequeños del ángulo
de incidencia, los coeficientes de reflexión paralelo y perpendicular
son iguales. Lo mismo pasa con los coeficientes de transmisión.
- Valores negativos. La presencia de estos valores en los
coeficientes
indica que el sentido arbitrario que atribuimos a los campos al hacer
la deducción
de las fórmulas de Fresnel no es apropiado en este caso.
- Para ángulos superiores al límite, no existe onda
transmitida.
- La amplitud transmitida puede superar el valor de la
incidente. Esto
no viola ningún principio de conservación, ya que no debe confundirse
la amplitud de la onda con su energía, la cual, obviamente, si se
conservará.
Además se puede verificar que
|
|
(2.46) |
 , |
donde los coeficientes 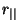 , , , ,  y y  se calculan pasando la luz del medio de índice
se calculan pasando la luz del medio de índice  al de al de  ,
mientras que
los coeficientes ,
mientras que
los coeficientes  , ,
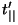 , , 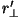 y y  se calculan haciendo el paso en sentido inverso, es decir, de
se calculan haciendo el paso en sentido inverso, es decir, de  a a  . .
2.3.3.1 Estudio de los
casos de incidencia rasante y normal
El estudio de los cambios de signo en el
factor de reflexión paralelo
debe ser realizado con atención. Analizaremos los casos extremos de
incidencia rasante (  ) e incidencia normal ( ) e incidencia normal ( ). Es necesario tener
presente
las figuras 2.8 y
2.9. ). Es necesario tener
presente
las figuras 2.8 y
2.9.
- CASO A:
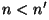 : :
- Incidencia normal. Los coeficientes de reflexión
paralelo
y perpendicular son negativos; el vector campo eléctrico reflejado
apunta siempre en sentido contrario al del dibujo (véanse
las figuras 2.8 y
2.9).
Observamos que entre el campo incidente y el reflejado hay un cambio de
fase
 para los
casos para los
casos 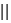 y
y 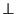 . .
- Incidencia rasante. El coeficiente paralelo es
positivo, por lo
tanto el sentido del vector es correcto. En el caso perpendicular
el sentido no es correcto. Por lo tanto, el campo incidente y el
reflejado están siempre en oposición de fase. Por tanto,
si extrapolamos estos argumentos para ángulos de incidencia
intermedios, se puede inferir que siempre se tiene un cambio de fase
 en la reflexión. en la reflexión.
- Transmisión. Los coeficientes son siempre positivos. No
hay
ningún cambio en la orientación arbitraria de los
vectores y, por lo tanto, podemos asegurar nunca hay cambio de fase
 . .
- CASO B:
 :
Haciendo el mismo razonamiento
que en el caso anterior, podemos asegurar que, en estas condiciones,
nunca se produce un salto de fase :
Haciendo el mismo razonamiento
que en el caso anterior, podemos asegurar que, en estas condiciones,
nunca se produce un salto de fase  , ni en reflexión ni en refracción. , ni en reflexión ni en refracción.
2.3.4 Factores de transmisión
y reflexión en intensidad
Definimos los factores de transmisión
como el cociente entre
la intensidad transmitida y la incidente. Es necesario definir un
factor
para la componente paralela y otro para la perpendicular. Recordemos
que
la intensidad se define como la media temporal de la energía radiada
por unidad de tiempo y de superficie. La definición de intensidad
exige que la detección se realice con un detector situado normalmente
a la dirección de propagación Recordemos que la intensidad
detectada vale: . .
Figura 2.12:
Obtención
de los factores de transmisión en intensidad
|
|
Consideremos la situación de la figura 2.12.
Una onda plana incide sobre una superficie de separación de medios
con un ángulo  respecto
a la normal y se refracta formando un ángulo respecto
a la normal y se refracta formando un ángulo  . La comparación entre los vectores de Poynting
se hará en la superficie de separación de los medios, aplicando
el principio de conservación de la energía. . La comparación entre los vectores de Poynting
se hará en la superficie de separación de los medios, aplicando
el principio de conservación de la energía. 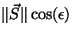 es la energía
que incide en la superficie de separación por unidad de superficie.
Análogamente, es la energía
que incide en la superficie de separación por unidad de superficie.
Análogamente,  es
la energía transmitida. Por lo tanto, el factor de transmisión
en intensidad de la componente paralela será es
la energía transmitida. Por lo tanto, el factor de transmisión
en intensidad de la componente paralela será
 |
(2.47) |
y, para la componente perpendicular,
 . . |
(2.48) |
Si consideramos el factor de reflexión, 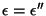 y y  , y por lo tanto, se puede
escribir , y por lo tanto, se puede
escribir
 . . |
(2.49) |
Como es natural, se debe verificar que
 |
(2.50) |
y, en el caso de incidencia normal,
 . . |
(2.51) |
2.3.5 Estudio de la reflexión
total
Cuando la luz llega a una superficie de
separación de medios (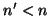 )
con un ángulo superior al
ángulo límite, toda la luz vuelve al primer medio. Recordemos
que el ángulo límite se obtiene cuando se verifica que )
con un ángulo superior al
ángulo límite, toda la luz vuelve al primer medio. Recordemos
que el ángulo límite se obtiene cuando se verifica que  . Definamos . Definamos  como, como, 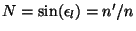 . La ley de
Snell
tiene un claro significado geométrico cuando trabajamos con medios
dieléctricos y en las condiciones habituales. Podemos hacer la
hipótesis
siguiente: la ley de la refracción tiene una validez formal más
allá de su significado intuitivo. Consideremos una onda plana incidente
sobre una superficie de separación de medios con un ángulo . La ley de
Snell
tiene un claro significado geométrico cuando trabajamos con medios
dieléctricos y en las condiciones habituales. Podemos hacer la
hipótesis
siguiente: la ley de la refracción tiene una validez formal más
allá de su significado intuitivo. Consideremos una onda plana incidente
sobre una superficie de separación de medios con un ángulo
 y y  . Aceptando la validez formal de la ley de Snell
podremos
escribir . Aceptando la validez formal de la ley de Snell
podremos
escribir 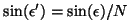 . En
el estudio que estamos realizando, . En
el estudio que estamos realizando,  , y el valor de , y el valor de  será, por lo tanto, será, por lo tanto,
 , , |
(2.52) |
 es una magnitud imaginaria. Más
adelante,
por consideraciones de conservación de la energía, se despreciará
el signo es una magnitud imaginaria. Más
adelante,
por consideraciones de conservación de la energía, se despreciará
el signo 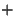 . Conociendo el valor de . Conociendo el valor de  y de y de  podemos aplicar ahora las
fórmulas de Fresnel. Analizando la figura 2.11, puede comprobarse que los factores de
reflexión perpendicular y paralelo toman el valor podemos aplicar ahora las
fórmulas de Fresnel. Analizando la figura 2.11, puede comprobarse que los factores de
reflexión perpendicular y paralelo toman el valor 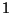 y y 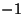 respectivamente,
para ángulos de incidencia superior al límite. Podemos estudiar
con mayor detalle estos valores del ángulo de incidencia: las fórmulas
del factor de reflexión para los dos casos de polarización
son:
respectivamente,
para ángulos de incidencia superior al límite. Podemos estudiar
con mayor detalle estos valores del ángulo de incidencia: las fórmulas
del factor de reflexión para los dos casos de polarización
son:
 ,
Puesto que conocemos los valores de 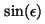 , , 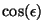 , ,  y y  , podemos escribir las
fórmulas
de Fresnel en términos de valores conocidos. Después de hacer
unas cuántas operaciones obtenemos que: , podemos escribir las
fórmulas
de Fresnel en términos de valores conocidos. Después de hacer
unas cuántas operaciones obtenemos que:
 . . |
(2.53) |
Éste es un resultado interesante: los coeficientes de reflexión
son complejos y de módulo 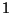 .
El valor de la amplitud no varía pero la onda incidente y reflejada
estén desfasadas. La onda reflejada paralela tendrá por ecuación .
El valor de la amplitud no varía pero la onda incidente y reflejada
estén desfasadas. La onda reflejada paralela tendrá por ecuación
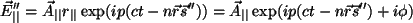 , , |
(2.54) |
mientras que la componente perpendicular será
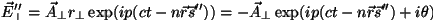 . . |
(2.55) |
La onda reflejada estará polarizada eliptícamente y sus componentes
estarán desfasadas 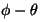 .
Este
desfase depende de .
Este
desfase depende de  y y  y puede variarse en función del
ángulo de incidencia y puede variarse en función del
ángulo de incidencia  . .
Figura 2.13:
Reflexión
total
|
|
Figura 2.14:Reflexión
total frustrada
|
|
¿Tiene sentido hablar de luz transmitida? A
simple vista, puesto que
toda la luz vuelve al primero medio, parece una pregunta sin sentido.
No obstante,
intentemos escribir la onda en el segundo medio:
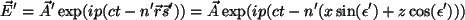 . . |
(2.56) |
También podemos escribir el valor de  y y  en términos del en términos del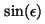 , ,
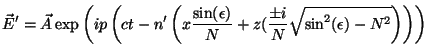 |
(2.57) |
y operando,
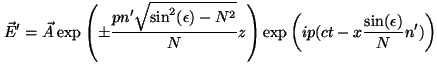 . . |
(2.58) |
La interpretación de esta ecuación es la siguiente:
- El término de amplitud presenta una caída exponencial
a medida que se penetra en el segundo medio. Despreciamos el signo
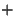 de la exponencial real ya que se trata
de una solución sin sentido físico, que daría lugar
a una onda que aumentaría indefinidamente su amplitud. de la exponencial real ya que se trata
de una solución sin sentido físico, que daría lugar
a una onda que aumentaría indefinidamente su amplitud.
- La dirección del vector de fase es
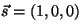 : la onda se
propaga en la interfase de los dos medios. : la onda se
propaga en la interfase de los dos medios.
El modelo demuestra la existencia de una onda
que penetra unas pocas longitudes
de onda en el segundo medio. Esto se corrobora experimentalmente
mediante
un fenómeno denominado Reflexión total frustrada o Efecto
Túnel Óptico: cuando el segundo medio es una lámina
de grosor muy pequeño, y se envía una onda con un ángulo
superior al límite, se puede observar que ésta se transmite
completamente sin reflejarse. La explicación satisfactoria de este
fenómeno debe buscarse en la Física Cuántica, que elimina
las inconsistencias de nuestro razonamiento: la onda de la interfase es
la
misma que después se detecta como reflejada.
|


 ,
,