JOptics

El formalismo básico para describir los fenómenos electromagnéticos relacionados con la óptica ondulatoria son las ecuaciones de Maxwell. En el sistema CGS Gauss se escriben como:

$\displaystyle \vec{\nabla} \wedge \vec{H} = \frac{4 \pi \vec{j}}{c} + \frac{1}{c} \frac{\partial \vec{D}}{\partial t}$	(2.1)
$\displaystyle \vec{\nabla} \wedge \vec{E} =- \frac{1}{c} \frac{\partial \vec{B}}{\partial t}$
$\displaystyle \vec{\nabla} \vec{D} = 4 \pi \rho$
$\displaystyle \vec{\nabla} \vec{B} = 0 \vspace{5mm}$ ,

donde $\vec{H}$ es el campo magnético, $\vec{E}$ es el campo eléctrico, $\vec{D}$ es el vector desplazamiento, $\vec{B}$ es el vector inducción magnética, $\vec{j}$ es la densidad de corriente, $\rho$ es la densidad de carga y

es una constante de proporcionalidad. Las ecuaciones de Maxwell se complementan con las denominadas relaciones constitutivas:

$\begin{displaymath} \vec{D}=\epsilon\vec{E} \qquad \vec{B}=\mu\vec{H} \qquad \vec{j}=\sigma\vec{E} \vspace{5mm} \end{displaymath}$ ,

(2.2)

donde $\epsilon$ es la constante dieléctrica, $\mu$ es la permeabilidad magnética y $\sigma$ es la conductividad eléctrica. En un medio dieléctrico homogéneo, isótropo y sin carga, $\rho=0$ , $\sigma = 0$ , $\epsilon$ y $\mu=$ constantes. Las ecuaciones se simplifican:

$\displaystyle \vec{\nabla} \wedge \vec{H} = \frac{\epsilon}{c} \frac{\partial \vec{E}}{\partial t}$	(2.3)
$\displaystyle \vec{\nabla} \wedge \vec{E} =- \frac{\mu}{c} \frac{\partial \vec{H}}{\partial t}$
$\displaystyle \vec{\nabla} \vec{E} = 0$
$\displaystyle \vec{\nabla} \vec{H} = 0 \vspace{5mm}$ .

Cuando un campo electromagnético cambia de medio, las componentes normales y tangenciales de éste verifican las relaciones siguientes:

$\displaystyle \textrm{Componentes normales:} \quad \vec{n}(\vec{D_2} - \vec{D_1}) = 4 \pi \rho_{s} \quad \vec{n}(\vec{B_2} - \vec{B_1}) = 0$	(2.4)
$\displaystyle \textrm{Componentes tangencials:} \quad \vec{n} \wedge (\vec{E_2}... ...vec{n} \wedge (\vec{H_2} - \vec{H_1}) = \frac{4\pi}{c} \vec{j}_{s} \vspace{5mm}$ ,

donde $\vec{n}$ es el vector normal a la superficie, y $\rho_{s}$ y $\vec{j}_{s}$ son las densidades superficiales de carga y de corriente, respectivamente. Los subíndices 1 y 2 hacen referencia a los campos en el medio original y en el medio en el que se transmiten los campos, respectivamente. Si las densidades de carga y corriente son cero, $\rho_{s} = 0$ y $\vec{j}_{s} = 0$ , entonces se verifican las siguientes relaciones de continuidad:

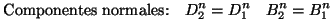$\displaystyle \textrm{Componentes normales:}\quad D_2^n = D_1^n \quad B_2^n = B_1^n$	(2.5)
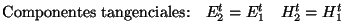$\displaystyle \textrm{Componentes tangenciales:}\quad E_2^t = E_1^t \quad H_2^t = H_1^t \vspace{5mm}$ .

En un medio homogéneo e isótropo, al combinar las ecuaciones de Maxwell se obtiene el par de ecuaciones siguiente:

$\displaystyle \Delta \vec{H} = \frac{\epsilon \mu}{c^2} \frac{\partial^2 \vec{H}}{\partial t^2}$	(2.6)
$\displaystyle \Delta \vec{E} = \frac{\epsilon \mu}{c^2} \frac{\partial^2 \vec{E}}{\partial t^2} \vspace{5mm}$ .

Estas expresiones son formalmente ecuaciones de ondas. Así, la velocidad de propagación puede relacionarse con los parámetros

, $\epsilon$ y $\mu$

$\begin{displaymath} \frac{1}{v^2} = \frac{\epsilon \mu}{c^2} \quad v = \frac{c}{\sqrt{\epsilon \mu}} \vspace{5mm} \end{displaymath}$ .

(2.7)

En el vacío, $\epsilon = \mu = 1$ , y por lo tanto

. Es decir,

es la velocidad de la luz en el vacío. El índice de refracción se puede escribir en función de los parámetros $\mu$ y $\epsilon$ , $n = c/v =\sqrt{\epsilon\mu}$ . Sean ${\vec r}=(x,y,z)$ el vector posición de un punto y ${\vec s}=(\alpha, \beta, \gamma)$ el vector unitario ( $\Vert{\vec s}\Vert = 1$ ) que indica la dirección de propagación de la onda. Se puede comprobar fácilmente que una función

del tipo $f(vt \pm {\vec r} {\vec s})$ es solución de la ecuación de ondas. Esta solución de la ecuación de ondas se denomina onda plana. En el caso unidimensional, escribiremos la ecuación de ondas como

$\begin{displaymath} \frac{\partial^2 {\vec E}}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 {\vec E}}{\partial t^2} \vspace{5mm} \end{displaymath}$ .

(2.8)

En este caso particular, 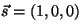${\vec s} = (1,0,0)$ , y la solución se escribe como

. De las relaciones entre la pulsación $\omega$ , el periodo

, $T=2 \pi/\omega$ , la longitud de onda $\lambda$ , el número de onda

, $k = 2 \pi/\lambda$ , la longitud de onda, la frecuencia $\nu$ y la velocidad, $\lambda \nu = v$ , podemos escribir el argumento de la función de onda plana como:

$\begin{displaymath} vt \pm {\vec r} {\vec s} = \frac{1}{k}(\omega t \pm k {\vec r} {\vec s}) \vspace{5mm} \end{displaymath}$ .

(2.9)

Dependiendo del caso que se estudie, la función

puede ser complicada de describir. El análisis de Fourier afirma que cualquier función puede ser descrita como una combinación lineal de funciones armónicas. Por esta razón, tomaremos funciones de onda armónicas para describir los campos eléctrico y magnético, por ejemplo:

$\begin{displaymath} {\vec E} = {\vec E_0} \cos(\omega t - k {\vec r}{\vec s}) \... ... {\vec H_0} \cos(\omega t - k {\vec r}{\vec s}) \vspace{5mm} \end{displaymath}$ ,

(2.10)

donde los módulos $\Vert{\vec E}_0\Vert$ y $\Vert{\vec H}_0\Vert$ son las amplitudes máximas de los campos eléctrico y magnético, respectivamente. El argumento de estas funciones es adimensional. Por comodidad, a la hora de hacer manipulaciones matemáticas, escribiremos los campos en notación compleja, aunque únicamente la parte real (o la imaginaria) tiene sentido físico, es decir:

$\begin{displaymath} {\vec E} = {\vec E_0} \exp (i(\omega t - k {\vec r}{\vec s}... ...vec H}_0 \exp(i(\omega t - k {\vec r}{\vec s})) \vspace{5mm} \end{displaymath}$ ,

(2.11)

${\vec E_0}$ es la amplitud de la onda y $\exp (i(\omega t - k {\vec r}{\vec s}))$ su fase, que también se puede escribir en términos del índice de refracción. Si definimos 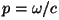$p=\omega/c$ , tendremos que

$\begin{displaymath} {\vec E} = {\vec E_0} \exp (ip(ct - n {\vec r}{\vec s})) \q... ... {\vec H}_0 \exp( ip(c t - n {\vec r}{\vec s})) \vspace{5mm} \end{displaymath}$ .

(2.12)

Definimos el concepto de frente de onda como el lugar geométrico de los puntos que tienen la misma fase, en un momento dado. En el caso de ondas planas, el frente de onda es el plano $k{\vec r}{\vec s} = C$ donde

es una constante. Es posible establecer una relación entre los conceptos de fase y camino óptico ( $\Delta = n l$ , donde

es el índice de refracción y

la distancia recorrida por la onda). Sea una onda de pulsación $\omega$ y dirección de propagación ${\vec s}$ . La diferencia de fase entre dos planos `

' y `

' del frente de onda, distantes

entre si, es

$\begin{displaymath} (\omega t - k{\vec r_2} {\vec s}) - (\omega t - k{\vec r_1}... ...s}) = k({\vec r_2}-{\vec r_1}) {\vec s} = k l \vspace{5mm} \end{displaymath}$ .

(2.13)

Si la onda se propaga en un medio de índice

, $kl = (k/n) nl = (k/n) \Delta = \frac{2 \pi}{\lambda n} \Delta= \frac{\lambda_0}{n} \Delta$ . Este resultado se utilizará más adelante en el estudio de los sistemas interferenciales. Otra solución de la ecuación de onda que presenta un gran interés es aquella en la que el valor de la amplitud de la onda sólo depende de la distancia al punto en que se genera. En este caso (onda esférica), es conveniente escribir la ecuación en coordenadas esféricas y quedarnos solo con la parte radial, es decir, ${\vec E} = {\vec E}(r,t)$ :

$\begin{displaymath} \Delta {\vec E} = \frac{1}{r} \frac{\partial^2 r {\vec E}}{... ...{v^2} \frac{\partial^2 {\vec E}}{\partial t^2} \vspace{5mm} \end{displaymath}$ ,

(2.14)

$\begin{displaymath} \frac{\partial^2 r {\vec E}}{\partial r^2} = \frac{1}{v^2} \frac{\partial^2 r {\vec E}}{\partial t^2} \vspace{5mm} \end{displaymath}$ .

(2.15)

Esta última expresión es formalmente idéntica a la ecuación de ondas en una dimensión escrita en coordenadas cartesianas. Por lo tanto, la solución en este caso será del tipo

$\begin{displaymath} {\vec E} = \frac{{\vec f}(vt \pm r)}{r} \vspace{5mm} \end{displaymath}$ .

(2.16)

**Figura 2.1:** Diferencia de fase
$\includegraphics[width=\linewidth]{Diffase.eps}$

**Figura 2.2:** Diferencia de fase (esquema transversal)
$\includegraphics[width=\linewidth]{Diffase2.eps}$

Introduciendo las soluciones de la ecuación de ondas para los campos eléctrico y magnético en las ecuaciones de Maxwell, podemos deducir las relaciones siguientes :

$\begin{displaymath} {\vec s} \wedge {\vec H} = - n {\vec E} \quad \quad \quad {\vec s} \wedge {\vec E} = \frac{{\vec H}}{n} \vspace{5mm} \end{displaymath}$ ,

(2.17)

relaciones que indican que los vectores campo eléctrico, campo magnético y el vector ${\vec s}$ son ortogonales entre si. Los vectores campos eléctrico y magnético vibran en un plano que se propaga según la dirección ${\vec s}$ , tal y como se muestra en la figura 2.3. La energía electromagnética almacenada en un diferencial de volumen se escribe

$\begin{displaymath} du = \left [ \frac{1}{8 \pi} (\epsilon \Vert {\vec E}\Vert^2 + \mu \Vert {\vec H}\Vert^2) \right ] dv \vspace{5mm} \end{displaymath}$ ,

(2.18)

y por lo tanto, la variación por unidad de tiempo de energía electromagnética almacenada en un volumen V cerrado por una superficie S es

$\begin{displaymath} \frac{\partial u }{\partial t}= \frac{\partial}{\partial t}... ...mu \Vert {\vec H}\Vert^2) \right ] \right ] dv \vspace{5mm} \end{displaymath}$ .

(2.19)

**Figura 2.3:** Transversalidad de los campos eléctrico y magnético
$\includegraphics[width=14cm]{ones.eps}$

Consideremos un material dieléctrico ideal ( $\sigma = 0$ ). Utilizando las ecuaciones de Maxwell podemos demostrar que la variación de energía puede expresarse como

$\begin{displaymath} \frac{\partial u }{\partial t}= - \frac{c}{4 \pi}\int_S {\vec E} \wedge{\vec H} ds \vspace{5mm} \end{displaymath}$ .

(2.20)

$\begin{displaymath} {\vec S} = \frac{c}{4 \pi}{\vec E} \wedge{\vec H} \vspace{5mm} \end{displaymath}$ .

(2.21)

El vector de Poynting expresa la variación de energía radiada por unidad de tiempo y de superficie perpendicular a la dirección de propagación. En los medios homogéneos e isótropos el vector de Poynting y el vector ${\vec s}$ tienen la misma dirección. La dirección del rayo (concepto propio de la Óptica Geométrica) y ${\vec S}$ (asociado a la propagación de la energía de la onda) coinciden. Si la longitud de onda corresponde al espectro visible (400-700 nm) el periodo de vibración es del orden de $10^{-14}$ s. Cuando colocamos un detector (célula fotoeléctrica, cámara de vídeo, ojo) ante una onda electromagnética, éste no es capaz de seguir las oscilaciones y por lo tanto detecta un promedio temporal de la señal. Así, definimos la intensidad del campo eléctrico como la media temporal del vector de Poynting.

$\begin{displaymath} I = <\Vert{\vec S}\Vert> = \lim_{\tau \rightarrow \infty} \frac{1}{\tau} \int_0^\tau \Vert{\vec S}\Vert dt \vspace{5mm} \end{displaymath}$ .

(2.22)

$\begin{displaymath} I = \frac{cn}{8 \pi} \Vert E_0\Vert^2 \vspace{5mm} \end{displaymath}$ ,

(2.23)

$\begin{displaymath} I = \frac{cn}{8 \pi} \frac{\Vert E_0\Vert^2}{r^2} \vspace{5mm} \end{displaymath}$ ,

(2.24)