JOptics

Consideremos un medio que presenta conductividad $\sigma \neq 0$ . Los metales tienen valores de $\sigma$ muy altos, pero los dieléctricos reales también pueden tener conductividades diferentes de cero. Si este medio es, además, no magnético ( $\mu = 1$ ) y sin densidad volumétrica de carga ( $\rho=0$ ), las ecuaciones de Maxwell se escriben

$\displaystyle \vec{\nabla} \wedge \vec{H} = \frac{4 \pi}{c} \sigma {\vec E}+ \frac{\epsilon}{c} \frac{\partial \vec{E}}{\partial t}$	(2.59)
$\displaystyle \vec{\nabla} \wedge \vec{E} =- \frac{\mu}{c} \frac{\partial \vec{H}}{\partial t}$
$\displaystyle \vec{\nabla} \vec{E} = 0$
$\displaystyle \vec{\nabla} \vec{H} = 0 \vspace{5mm}$ ,

donde $\vec{j}=\sigma\vec{E}$ . Podemos ensayar el uso de una onda armónica, ${\vec E}={\vec E_0}e^{i(\omega t -k {\vec r}{\vec s})}$ , como solución de las ecuaciones de Maxwell en medios con conductividad. La derivada temporal de una onda armónica es proporcional a ella misma,

$\begin{displaymath} \frac{\partial {\vec E}}{\partial t} = i \omega {\vec E_0}e... ...ga t -k {\vec r}{\vec s})} = i \omega {\vec E} \vspace{5mm} \end{displaymath}$ .

(2.60)

$\begin{displaymath} \vec{\nabla} \wedge \vec{H} = (-\frac{4 \pi \sigma}{\omega}... ...frac{1}{c} \frac{\partial \vec{E}}{\partial t} \vspace{5mm} \end{displaymath}$ ,

(2.61)

que es formalmente idéntica a la ecuación de Maxwell que se aplica en el caso de medios dieléctricos. Es necesario hacer la identificación de la permeabilidad dieléctrica $\epsilon$ con una función de la permeabilidad generalizada ${\hat \epsilon}=\epsilon-\frac{4 \pi \sigma}{c} i$ . Si $\sigma = 0$ , obtenemos de nuevo la permeabilidad ordinaria de los medios dieléctricos ideales. 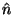Podemos calcular también el índice de refracción generalizado ${\hat n}$ , a partir de la relación ${\hat n}^2 = {\hat \epsilon}$ . El índice complejo es ${\hat n} = n -i\kappa$ , donde

es el índice de refracción ordinario y $\kappa$ es el denominado coeficiente de extinción. Identificando términos y aislando adecuadamente podemos escribir

$\displaystyle n= \left [ \frac{\epsilon}{2} + \sqrt{\frac{\epsilon^2}{4} + \frac{4 \pi^2 \sigma^2}{\omega^2}} \right ] ^{1/2}$	(2.62)
$\displaystyle \kappa= \left [ -\frac{\epsilon}{2} + \sqrt{\frac{\epsilon^2}{4} + \frac{4 \pi^2 \sigma^2}{\omega^2}} \right ] ^{1/2}$ .

$\begin{displaymath} n \approx \kappa \approx \sqrt{2\pi \sigma / \omega} \vspace{5mm} \end{displaymath}$ ,

(2.63)

fórmula conocida como la relación de Drude. La solución a la ecuación de ondas en un medio con $\sigma \neq 0$ será

$\begin{displaymath} {\vec E}={\vec E_0}e^{ip(ct-{\hat n} {\vec r}{\vec s})} = {... ...p {\vec r}{\vec s}}e^{ip(ct-n{\vec r}{\vec s})} \vspace{5mm} \end{displaymath}$ .

(2.64)

Vemos que es una ecuación similar a la que se obtiene cuando las ondas se propagan libremente en un medio dieléctrico. Sin embargo, la amplitud decae exponencialmente a medida que la onda se propaga. Analicemos como se transmite una onda electromagnética desde un medio dieléctrico a un medio metálico. En esta sección utilizaremos los ángulos $\theta$ i $\theta'$ para referirnos a los ángulos de incidencia y refracción, para evitar confusiones con la permeabilidad dieléctrica $\epsilon$ . Aplicando las condiciones de contorno en un cambio de medio, podríamos deducir de nuevo la fórmula de Snell de la refracción, para este caso. Lo que obtendríamos es una expresión de aspecto familiar,

$\begin{displaymath} n \sin(\theta) = {\hat n'} \sin({\hat \theta'}) \vspace{5mm} \end{displaymath}$ ,

(2.65)

aunque notablemente diferente en cuanto a su interpretación. Ahora, el índice del segundo medio es complejo y ${\hat \theta'}$ es también complejo. El producto ${\hat n'} \sin({\hat \theta'})$ es real, pero ${\hat n'} \cos({\hat \theta'}) = a -bi$ , en general, no lo será. La onda en el segundo medio se escribirá

$\begin{displaymath} {\vec E'}={\vec E_0} e^{ip(ct-{\hat n'}{\vec r}{\vec s})} =... ...(x\sin({\hat \theta'})+z\cos({\hat \theta'})))) \vspace{5mm} \end{displaymath}$ ,

(2.66)

$\begin{displaymath} {\vec E'}={\vec E_0} e^{ip(ct-{\hat n'}{\vec r}{\vec s})}= ... ...} e^{ip(ct-(x n \sin(\theta)+z a ))} e^{-pb z} \vspace{5mm} \end{displaymath}$ .

(2.67)

La onda se amortigua rápidamente a medida que penetra en un medio conductor. Además, la onda se propaga en la dirección ${\vec s}'=(n\sin(\theta), 0 , a)$ . Por lo tanto, el ángulo de refracción (con sentido físico) es

$\begin{displaymath} \tan(\theta') = \frac{n\sin(\theta)}{a} \vspace{5mm} \end{displaymath}$ .

(2.68)

Por otra parte, la mayor parte de la luz se refleja. Por ejemplo, si calculamos el factor de reflexión

para incidencia normal desde el aire a un metal, se obtiene

$\begin{displaymath} R = \Vert \frac{1-\hat n}{1+\hat n} \Vert^2 \approx 1 - \frac{2}{\sqrt{\sigma T}} \approx 1 \vspace{5mm} \end{displaymath}$ .

(2.69)

Esto explica la razón por la que se utilizan recubrimientos metálicos para fabricar espejos.