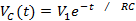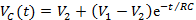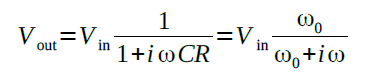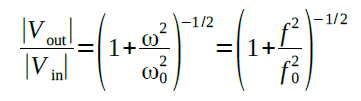11 TRANSITORI RC. FILTRE RC PASSA-BAIXOS

Resum. En aquesta pràctica s’estudiarà com varia la tensió d’un condensador quan se’l descarrega a través d’una resistència R, observant el comportament exponencial de l’evolució de la tensió respecte del temps. Es definirà un paràmetre important, la constant de temps, τ, i s’estudiarà com mesurar-la. Es comprovarà com la funció exponencial també governa els canvis de tensió en el condensador quan s’aplica una tensió quadrada a un circuit RC. Finalment s'estudiarà el sistema RC com a filtre de freqüències.

12.1 Fonament

12.1.1 Càrrega i descàrrega d’un condensador

Quan tenim un condensador de capacitat C carregat a una tensió inicial V₁ i el descarreguem a través d’una resistència R, la variació en el temps de la tensió entre les armadures del condensador segueix l’expressió:

El producte RC, que té dimensions de temps, s’acostuma a designar per constant de temps, τ.

Anàlogament, si el que tenim és un condensador carregat a una tensió inicial V₁ i el carreguem aplicant-li una diferència de potencial V₂, com a conseqüència de l’existència d’una resistència en el circuit mateix, la tensió entre les armadures evoluciona com:

Fàcilment es veu com V_c(t) evoluciona de V₁ a V₂ de manera anàloga a la descàrrega.

12.1.2 Càrregues successives per aplicació d’un senyal quadrat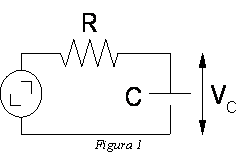

Si apliquem una tensió quadrada a un condensador C a través d’una resistència R (figura 1), la tensió del condensador variarà en el temps de manera que intentarà ‟seguir” la tensió aplicada (figura 2). La transició des de V₁ cap a V₂ (i semblantment la de V₂ cap a V₁) presenta una dependència exponencial decreixent donada per (2).

En el cas particular d’un senyal quadrat que va des de V₀ fins a -V₀, tenim que V₁ = V₀ i V₂ = -V₀.

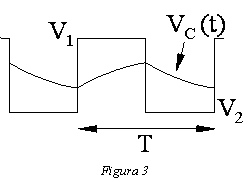
Si RC és prou petit (un factor 5 és suficient) comparat amb T/2, el condensador pràcticament arriba a assolir la tensió final, V₂ i la V_C(t) mostra un aspecte semblant a la figura 2. Si no és així, es produeixen situacions com la de la figura 3.

12.1.3 Filtre elèctric RC passa-baixos

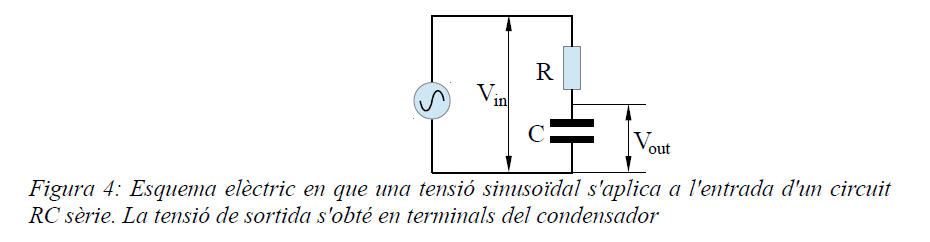
El fenomen de la càrrega i descàrrega d'un condensador constitueix la base dels filtres elèctrics RC. La figura mostra un generador aplicant una tensió alterna sinusoïdal, d'amplitud V_in, a la composició en sèrie d'un condensador i una resistència. El formalisme del corrent altern mostra que la tensió a la sortida és

i que, per tant, el quocient entre les amplituds és

on f₀ = ω₀ (2π)^-1= (2πRC)^-1 rep el nom de freqüència de tall del filtre. Aquestes expressions mostren que, quan la freqüència de la tensió a l'entrada és prou baixa comparada amb f₀, la tensió a la sortida és, aproximadament, la mateixa que la de l'entrada, |V_out|/|V_in| ≈ 1 (el condensador té temps de carregar-se i descarregar-se). En canvi, per a freqüències altes, l'amplitud de la tensió de sortida és inversament proporcional a la freqüència |V_out|/|V_in| ≈ f₀/f.

12.2 Dispositiu experimental

Primera part:

• 1 placa RC-1 amb un condensador gran, una resistència elevada i un commutador

• 1 cronòmetre

• 1 voltímetre digital

• 1 alimentador de V ≅ +3V

Segona part:

• 1 placa RC-2 amb dues resistències i dos condensadors

• 1 oscil·loscopi digital

• 1 generador de funcions

12.3 Procediment experimental

L’objecte de la pràctica és l’estudi de la càrrega i descàrrega d’un condensador a través d’una resistència, observant l’evolució de la tensió del condensador en funció del temps. A partir de la variació observada, es determinarà el valor de la constant de temps del circuit, i, a partir d’aquesta, el valor de la capacitat.

12.3.1 Descàrrega d’un condensador (1a. part)

Endolleu l’alimentador de V ≅ +3V del circuit RC-1 i connecteu el voltímetre digital als extrems del condensador. Connecteu el commutador a la posició C (càrrega). El condensador es carregarà ràpidament fins a la tensió de l’alimentador V₁. Anoteu el valor de la tensió (V₁) en el full de mesures (t = 0). Passeu el commutador a la posició D (descàrrega), al mateix temps que poseu en marxa el cronòmetre. Anoteu en el full de mesures els valors de la tensió del condensador donada pel voltímetre a intervals de 10 segons (30 lectures). El condensador s’ha descarregat a través de la resistència del circuit.

A partir de les dades, calculeu ln V(t) i representeu aquests valors en una gràfica en funció del temps. Feu una regressió lineal, i obteniu la constant de temps del circuit RC. Un mètode més curt, però més imprecís, per calcular τ és el següent: determineu sobre la gràfica anterior el temps que ha trigat el condensador a passar d’una tensió qualsevol, V, a V/e. Aquest temps és la constant de temps del circuit.

Coneixent el valor de la resistència de descàrrega R, i amb el valor de τ obtingut, calculeu la capacitat del condensador i compareu-la amb la nominal (anotada al condensador).

12.3.2 Càrregues successives per aplicació d’un V(t) de forma quadrada (2a part)

Si la constant de temps d’un circuit és curta, no és possible utilitzar un cronòmetre per prendre mesures de la descàrrega del condensador. En aquest cas s’aplica al circuit un senyal quadrat repetitiu, de freqüència adequada i s’observa la descàrrega periòdica del condensador a la pantalla d’un oscil·loscopi.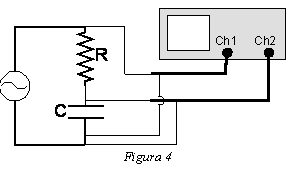

En la placa RC-2 munteu el circuit de la figura 4, amb R = 10 kΩ i C = 10 nF. Al muntar el circuit tingueu cura de connectar totes les terres en comú.

Ajusteu la freqüència del generador a 1 kHz. Visualitzeu tots dos canals en pantalla i ajusteu els controls de l’oscil·loscopi per tal de veure més d’un cicle complet de càrrega i descàrrega. Amb els controls de base de temps i d’amplificació del canal 2, tracteu d’obtenir sobre la pantalla una imatge semblant a la figura 5.

Ajudant-vos dels cursors mòbils de l’oscil·loscopi (dos de tensió i dos de temps), obteniu una col·lecció de valors V(t). Preneu com a origen de tensions el valor asimptòtic al qual tendeix V(t). Mesureu, almenys, 15 punts. Calculeu τ amb el mateix tractament de dades que l’efectuat en l’apartat 12.3.1.

Un mètode més curt, però més imprecís, per calcular τ és el següent: determineu sobre la pantalla de l’oscil·loscopi, amb l’ajut dels cursors, el temps que ha trigat el condensador a passar d’una tensió qualsevol, V, a V/e. Aquest temps és la constant de temps del circuit.

Compareu els valors de τ obtinguts amb el del producte de R i C (no oblideu que a R cal sumar la resistència interna del generador de 50 Ω). Tingueu en compte la incertesa en mesurar τ.

12.3.3 Filtre RC passa-baixos

Munteu el circuit de la figura 4. Configureu el generador perquè proporcioni tensions sinusoïdals d'uns 5 V d'amplitud. Començant per f=100 Hz, i fins a f=20000 Hz, preneu mesures de la freqüència i la tensió en el condensador (a raó de, aproximadament, tres freqüències per dècada).

12.4 Realització de l’informe

1. Representeu les dades V_C(t) obtingudes a l'apartat 12.3.1 en una gràfica on l'eix de les V estigui en escala logarítmica i el temps en escala lineal. Feu l'ajust numèric per a obtenir la constant de temps, RC, del circuit i, a partir d'ella i del valor de R₁, calculeu el valor de C₁ i compareu-lo amb la capacitat que hi ha anotada al propi condensador.

2. Representeu les dades V_C(t) obtingudes a l'apartat 12.3.2 en una gràfica on l'eix de les V estigui en escala logarítmica i el temps en escala lineal. Feu l'ajust numèric per a obtenir la constant de temps, RC, del circuit i, a partir d'ella i del valor de R₂ (al qual cal sumar els 50Ω de la impedància del generador AC), calculeu el valor de C₂ i compareu-lo amb la capacitat que hi ha anotada al propi condensador.

3. Representeu les dades V_C(ω) obtingudes a l'apartat 12.3.3 en una gràfica on els eixos estiguin en escala logarítmica (diagrama de Bode del filtre). Obteniu el valor de ω₀ i compareu-lo amb el producte RC obtingut a l'apartat 2.

4. Demostreu que el producte RC té dimensions de temps.

5. Calculeu el temps que ha de passar, mesurat en termes de la constant de temps, perquè la tensió d’un condensador, en descarregar-se, arribi a un 1 % de la tensió inicial.

6. A partir del resultat de la qüestió anterior, indiqueu quina limitació existeix en el valor màxim de la freqüència del senyal quadrat, per a un valor determinat de R i C, si es vol mesurar la constant de temps.