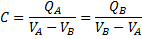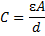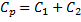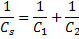- 1. ESTUDI D'UN CONDENSADOR
- 2 CONSTRUCCIÓ I CONNEXIÓ D’APARELLS DE MESURA
- 3. CARACTERÍSTICA ELÈCTRICA D'UNA CÈL·LULA SOLAR
- 4. CONDUCTIVITAT ELÈCTRICA
- 5. CREACIÓ DE CAMP MAGNÈTIC
- 6. MESURA DEL CAMP MAGNÈTIC TERRESTRE
- 7. MATERIALS FERROMAGNÈTICS. CICLE D'HISTÈRESI.
- 8. INDUCCIÓ ELECTROMAGNÈTICA I CORRENTS DE FOUCAULT
- 9. TENSIONS ALTERNES: AMPLITUD, VALOR EFICAÇ, FREQÜÈNCIA, DESFASAMENT. SUMA DE TENSIONS
- 10. CORRENT ALTERN. IMPEDÀNCIES I RESSONÀNCIA.
- 11. TRANSITORI RC. FILTRE RC OASSA-BAIX
- OLD. DEPENDÈNCIA DE LA RESISTIVITAT AMB LA TEMPERATURA
Menú principal
Se encuentra usted aquí
1 ESTUDI D'UN CONDENSADOR
Resum. El quocient entre la càrrega emmagatzemada per un condensador i la diferència de potencial entre armadures és una constant que és característica de cada condensador i s’anomena capacitat. En aquest treball s’estudia, en primer lloc, aquesta proporcionalitat. Seguidament s’analitzen les lleis d’associació de condensadors (sèrie i paral·lel). Finalment s’estudia detalladament un condensador pla.
1.1 Fonament
Un condensador està format per dos conductors (A i B, anomenats armadures) en influència total. En un condensador la càrrega que emmagatzema l’una o l’altra de les armadures i la diferència de potencial entre totes dues són proporcionals. El quocient entre elles és positiu i es coneix com a capacitat, C, del condensador:
|
|
(1) |
De la relació anterior es pot deduir que la capacitat equivalent de dos condensadors connectats en paral·lel és igual a la suma de les seves capacitats; i que la inversa de la capacitat equivalent de dos condensadors en sèrie és igual a la suma de les inverses de les capacitats respectives.
El càlcul de la capacitat d’un condensador pot ser resolt amb una certa facilitat en els casos de geometries senzilles. Per exemple, si es tracta de dues plaques paral·leles de superfície A, separades una distància d, la capacitat d’aquest condensador és:
|
|
(2) |
on ε és la permitivitat del medi que separa les dues plaques (ε0 = 10-9/36π F/m si és aire).
1.2 Dispositiu experimental
-
1 placa amb dos condensadors (C1 i C2)
-
1 font de tensió contínua
-
1 voltímetre digital
-
1 condensador pla (format per dos discos metàl·lics aïllats de 20 cm de diàmetre amb una separació que es pot variar)
-
1 coulombímetre.
Un coulombímetre està format, bàsicament, per un voltímetre de resistència d’entrada molt elevada i un condensador de capacitat elevada C connectat en paral·lel a l’entrada. A causa d’aquest fet, si el coulombímetre està descarregat i es connecta a un sistema carregat, n’absorbeix una part de la càrrega. Si la capacitat del sistema que es mesura és molt menor que la del coulombímetre, aquest rep pràcticament tota la càrrega en qüestió. De la lectura del voltímetre se’n calcula la càrrega absorbida: Q = CV. Funciona correctament per a la mesura de càrregues entre 10 i 1999 nC.
En el moment de fer una mesura (el coulombímetre ha d’haver estat curtcircuitat momentàniament per descarregar-lo i posar-lo a zero), connecteu el condensador del qual voleu mesurar la càrrega entre els terminals negatiu i positiu del coulombímetre. Un cop feta la mesura s’ha de curtcircuitar l’entrada del coulombímetre per preparar-lo per la mesura següent.
-
1 electròmetre.
L’electròmetre és un instrument que mesura diferències de potencial (similar a un voltímetre), amb la particularitat de tenir una resistència d’entrada molt més elevada (1014 Ω), cosa que permet mesurar la tensió d’un condensador sense descarregar-lo.
L’inconvenient principal dels electròmetres és que es poden avariar fàcilment. El motiu és que les càrregues estàtiques presents normalment (roba, aparells de plàstic, fibres, dielèctrics en general), tot i ser petites, sovint porten associats potencials elevats (superiors a 100 V). Si un cos amb càrregues estàtiques toca l’entrada d’un electròmetre, aquests potencials elevats fan malbé el transistor (FET de resistència molt elevada) que hi ha a l’entrada. Per evitar avaries cal prendre precaucions: no toqueu mai les armadures del condensador pla quan l’electròmetre estigui engegat.
Per tal de fer mesures amb l’electròmetre procediu de la següent manera:
-
Assegureu-vos que el selector de sota de l'interruptor POWER està en la posició "zero lock" abans d'engegar l'aparell.
-
Seleccioneu el rang de mesura de 100 V.
-
Gireu el botó a la posició "push to zero" per a fer les mesures. En aquesta posició, si premeu el botó curtcircuitareu l'entrada i obtindreu un zero per a ajustar el decalatge de zero que hi pugui haver. Deixeu anar el botó per a carregar el condensador i fer les mesures.
-
Premeu el botó vermell de la pantalla digital per a llegir la tensió en Volts.
1.3 Procediment experimental
1.3.1 Relació càrrega/tensió. Capacitat
Observem la proporcionalitat (1) entre la tensió aplicada a un condensador i la càrrega que emmagatzema. Per fer-ho, carreguem el condensador C a diferents tensions (posició 1 en el circuit de la figura 1) i seguidament en mesurarem la càrrega connectant-lo al coulombímetre (posició 2).
Un cop mesurada una càrrega i abans de mesurar la següent s’ha de descarregar el coulombímetre curtcircuitant-lo. Obtindrem així una col·lecció de mesures (Q, V), variant V entre 0 i 10 V (mínim 15 punts).
Aquest mètode té, però, un inconvenient: en mesurar la càrrega del condensador, aquest perd la seva càrrega. Per tant, en el nostre cas, després de cada mesura haurem de tornar a carregar el condensador; i també descarregar el coulombímetre, curtcircuitant l’entrada.
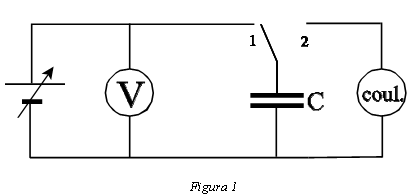
1.3.2 Associació en paral·lel
Mesureu la capacitat C1 i C2. Atès que ja hem vist que V i Q són proporcionals, n’hi ha prou amb una sola mesura (Q, V). Mesureu després la capacitat CP de l’associació en paral·lel de C1 i C2. Comproveu que els valors obtinguts compleixen la llei:
|
|
(3) |
1.3.3 Associació en sèrie
Determineu la capacitat (CS) de l’associació en sèrie de C1 i C2. Comproveu que els valors obtinguts compleixen la llei:
|
|
(4) |
1.3.4 Condensador pla
Munteu el circuit de la figura 2. Fixeu una separació d’1 mm entre armadures i carregueu el condensador a 10 V. Desconnecteu ara el condensador de la font: la càrrega de les armadures romandrà constant.
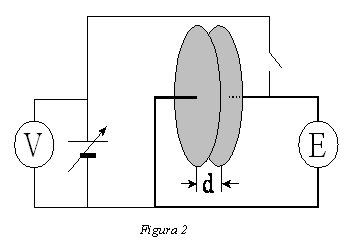
Varieu la separació entre armadures fins a 15 mm i anoteu les tensions. Per a l’elecció dels valors de d tingueu en compte que haureu de representar 1/V d’acord amb 1/d.
1.4 Realització de l’informe
Quan hàgiu anotat al full de laboratori tots els valors observats, feu els càlculs següents:
-
Amb els valors mesurats en l’apartat 1.3.1, feu una regressió lineal de la relació entre la càrrega i la tensió. Deduïu-ne el valor de la capacitat del condensador.
-
Comproveu que els resultats obtinguts en l’apartat 1.3.2 confirmen la llei d’associació de condensadors en paral·lel.
-
Comproveu que els resultats de l’apartat 1.3.3 confirmen la llei d’associació de condensadors en sèrie.
-
En l’apartat 1.3.4, la capacitat de l’electròmetre i del seu cable és del mateix ordre que la del condensador pla i no se’n pot prescindir. En realitat heu carregat aquest condensador de capacitat constant, Ce, en paral·lel amb un condensador de capacitat variable, funció de la distància entre les plaques, Cd. Aplicant a aquesta associació en paral·lel (Ceq = Cd + Ce) l’expressió general Q = CeqV, deduïu que 1/V és una funció lineal de 1/d, i que dels paràmetres que defineixen aquesta recta es pot obtenir la càrrega emmagatzemada i la capacitat de l’electròmetre Ce.
-
Calculeu la regressió de 1/V sobre 1/d i, sabent que el diàmetre de les plaques és de 20 cm, calculeu Q i Ce.