The Characteristic Stellar Mass
In the scenario of turbulent fragmentation, the characteristic stellar mass is essentially the Bonnor-Ebert mass at the characteristic postshock density (Padoan, Nordlund and Jones 1997, MNRAS 288, 145).
Bonnor-Ebert mass: isothermal sphere confined by external pressure (Ebert 1955; Bonnor 1956; McCrea 1957). It is a non-linear configuration (factor 14 density contrast).
With only thermal pressure:
Including the dynamic pressure of the turbulence (shocks --> non-linear density jumps):
So the modified turbulent Bonnor-Ebert mass is the mean B-E mass divided by the Mach number:
We test the theory with simulations:
i) without gravity to study the effect of the turbulence in isolation
Padoan et al. 2007 ApJ 661, 972
ii) with gravity and sink particles to test the combined effect of gravity, turbulence and dynamical interactions
Isothermal MHD Simulations
We test the theory (open circles and dotted blue line in the right panel) with isothermal MHD simulations with gravity and sink particles (see Haugbølle, Padoan and Nordlund 20017):
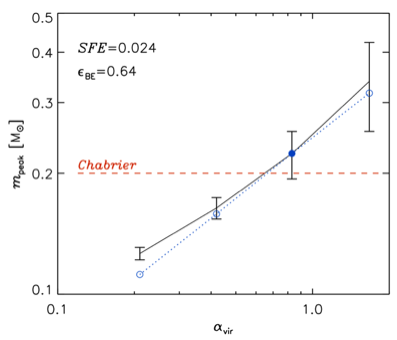
IMF peak mass versus virial parameter (only the mean density is varied).
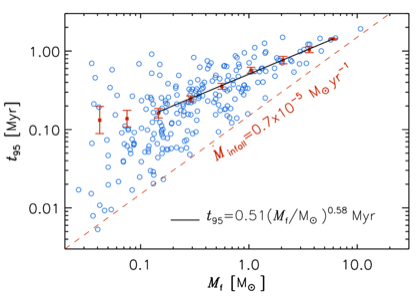
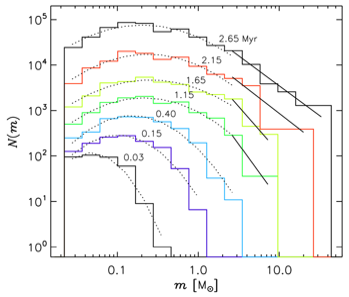
Early Time Evolution of the IMF
Because the final stellar mass takes some time to assemble (see the left panel), the stellar IMF exhibits a significant time evoluiton over the first ~1 Myr of star formation, with a gradual build up of the Salpeter power-law tail (see the right panel):
