| |
1.3
Telescopios
Subsecciones
1.3.1
Introducción
Los telescopios son instrumentos diseñados
por observar objetos muy
alejados. Se trata de sistemas afocales. Esto quiere decir que la
imagen
del infinito a través del telescopio está también en
el infinito. Al igual que el microscopio, los telescopios se diseñan
de forma que los rayos emergentes del instrumento salgan paralelos, es
decir,
hacia el infinito. De este modo, el ojo puede trabajar sin acomodación,
y por lo tanto no se fuerza la vista mientras se utiliza el
instrumento.
Finalmente, la imagen del infinito se proyecta sobre la retina. Los
telescopios
y los microscopios están formados básicamente por dos sistemas
ópticos: objetivo y ocular. El ocular del telescopio y del microscopio
funcionan de manera análoga. Se trata de un sistema de lentes tal
que en su plano focal objeto se forma la imagen producida por el
objetivo.
y, por lo tanto, ésta se proyecta de nuevo hacia el infinito (a través
del ocular).
1.3.2
Anteojo astronómico
El anteojo astronómico es el
telescopio más simple.
Consiste en dos sistemas de lentes convergentes: el objetivo, de focal 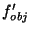 , y el ocular, con focal , y el ocular, con focal 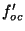 . El plano focal imagen del
objetivo
y el plano focal objeto del ocular son coincidentes. Así, los rayos
que provienen del infinito forman una imagen intermedia en el plano
focal
común. El ocular proyecta de nuevo esta imagen al infinito. La figura
1.29 muestra el
trazado de rayos a través
de un telescopio astronómico. Los rayos que entran paralelos al eje
óptico se cruzan en el punto focal imagen del objetivo; al atravesar
el ocular vuelven a salir paralelos al eje óptico. El rayo que entra
por el extremo superior del objetivo sale ahora por debajo,
indicándonos
de forma gráfica que este instrumento tendrá un aumento negativo.
Los rayos que entran en el sistema, formando un cierto ángulo . El plano focal imagen del
objetivo
y el plano focal objeto del ocular son coincidentes. Así, los rayos
que provienen del infinito forman una imagen intermedia en el plano
focal
común. El ocular proyecta de nuevo esta imagen al infinito. La figura
1.29 muestra el
trazado de rayos a través
de un telescopio astronómico. Los rayos que entran paralelos al eje
óptico se cruzan en el punto focal imagen del objetivo; al atravesar
el ocular vuelven a salir paralelos al eje óptico. El rayo que entra
por el extremo superior del objetivo sale ahora por debajo,
indicándonos
de forma gráfica que este instrumento tendrá un aumento negativo.
Los rayos que entran en el sistema, formando un cierto ángulo con el eje óptico se
cruzarán
en un cierto punto del plano focal común. Para determinar este punto
hay que recordar que el rayo que pasa por el centro de la lente no se
desvía.
Al pasar los rayos a través del ocular, estos salen paralelos formando
un ángulo con el eje óptico se
cruzarán
en un cierto punto del plano focal común. Para determinar este punto
hay que recordar que el rayo que pasa por el centro de la lente no se
desvía.
Al pasar los rayos a través del ocular, estos salen paralelos formando
un ángulo  con el
eje óptico. Para determinar la dirección de salida, se ha indicado
con línea discontinua un rayo auxiliar que pasa por el punto del plano
focal donde se han cruzado los rayos que entran en el sistema formando
un
ángulo con el
eje óptico. Para determinar la dirección de salida, se ha indicado
con línea discontinua un rayo auxiliar que pasa por el punto del plano
focal donde se han cruzado los rayos que entran en el sistema formando
un
ángulo  con el
eje óptico y que pasa sin desviarse por el centro del ocular. En el
plano focal común, se suele colocar el diafragma de campo. El tamaño
de la imagen del infinito que se forma en este plano está limitada
por las dimensiones de este diafragma. El tamaño de este objeto
intermedio
es una medida directa del ángulo máximo que puede penetrar
en el telescopio. Por otra parte, la limitación sobre la cantidad
de luz que penetra en el sistema (diafragma de apertura, DA) se
encuentra
en el objetivo. Como que no tenemos ningún sistema óptico previo
al objetivo, éste se comporta como la pupila de entrada (PE) del
sistema.
Al calcular la imagen del DA a través del ocular, se obtiene la
posición
y las dimensiones de la pupila de salida (PS). Este es el plano donde
se
debe colocar el ojo para observar a través del anteojo (plano de
emergencia de pupila). Si nos fijamos en el trazado de rayos en
eje,
se podría pensar que cualquier plano a partir del ocular sería
adecuado para colocar el ojo. Sin embargo, al hacer el trazado en campo
puede
verse que la única manera de no perder rayos es colocar el ojo en
la PS. con el
eje óptico y que pasa sin desviarse por el centro del ocular. En el
plano focal común, se suele colocar el diafragma de campo. El tamaño
de la imagen del infinito que se forma en este plano está limitada
por las dimensiones de este diafragma. El tamaño de este objeto
intermedio
es una medida directa del ángulo máximo que puede penetrar
en el telescopio. Por otra parte, la limitación sobre la cantidad
de luz que penetra en el sistema (diafragma de apertura, DA) se
encuentra
en el objetivo. Como que no tenemos ningún sistema óptico previo
al objetivo, éste se comporta como la pupila de entrada (PE) del
sistema.
Al calcular la imagen del DA a través del ocular, se obtiene la
posición
y las dimensiones de la pupila de salida (PS). Este es el plano donde
se
debe colocar el ojo para observar a través del anteojo (plano de
emergencia de pupila). Si nos fijamos en el trazado de rayos en
eje,
se podría pensar que cualquier plano a partir del ocular sería
adecuado para colocar el ojo. Sin embargo, al hacer el trazado en campo
puede
verse que la única manera de no perder rayos es colocar el ojo en
la PS.
Figura 1.29:anteojo
astronómica
![\includegraphics[width=\textwidth]{teleastr.eps}](img133.gif) |
En los telescopios, el aumento viene dado por
la relación entre
lo que se ve a través del instrumento respecto el que se vería
a ojo desnudo
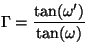 , , |
(1.16) |
el aumento obtenido con este sistema es
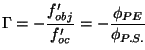 . . |
(1.17) |
Nótese que este aumento es negativo. La fórmula del aumento
se puede demostrar fácilmente a partir de equivalencias de triángulos
en la figura1.29.
1.3.3
Anteojo de Galileo
El anteojo de Galileo es un
instrumento con un diseño muy parecido
al anteojo astronómica. Este último presenta un aumento negativo
y por lo tanto genera un problema de orden práctico al utilizarlo
para observar objetos en la Tierra, ya que se ven las cosas invertidas.
Para conseguir un aumento positivo, se utiliza una lente o sistema
divergente
como ocular. El plano focal imagen del objetivo y el plano focal objeto
del ocular son también coincidentes. Las figuras 1.30 y 1.31 muestran
el trazado de rayos en eje y en campo. Es fácil demostrar que aquí
el aumento también se describe por
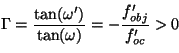 . . |
(1.18) |
Como el valor de 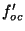 es negativo,
ya que la lente es divergente, el aumento visual del instrumento es
positivo.
Para encontrar la posición de la pupila de salida, se calcula la
posición
de la imagen de la montura del objetivo a través del ocular. Esta
se encuentra en el interior del telescopio, y en consecuencia el
objetivo
no actúa de diafragma de apertura. El ojo se deberá acercar
al máximo al ocular y mirar a través. La imagen del objetivo
limitará el campo que verá el ojo, por lo tanto, el objetivo
hace de diafragma de campo del conjunto telescopio-ojo y su imagen, de lucarna
de salida.
es negativo,
ya que la lente es divergente, el aumento visual del instrumento es
positivo.
Para encontrar la posición de la pupila de salida, se calcula la
posición
de la imagen de la montura del objetivo a través del ocular. Esta
se encuentra en el interior del telescopio, y en consecuencia el
objetivo
no actúa de diafragma de apertura. El ojo se deberá acercar
al máximo al ocular y mirar a través. La imagen del objetivo
limitará el campo que verá el ojo, por lo tanto, el objetivo
hace de diafragma de campo del conjunto telescopio-ojo y su imagen, de lucarna
de salida.
Figura 1.30:
Anteojo de Galileo
(trazado de rayos en eje)
|
|
Figura 1.31:Anteojo
de Galileo
(trazado de rayos en campo)
![\includegraphics[width=\textwidth]{37_9b.eps}](img138.gif) |
1.3.4 Anteojo terrestre
El anteojo terrestre es una
alternativa para conseguir telescopios
con aumento visual positivo sin que se generen los problemas de viñeteo
propios del anteojo de Galileo. Se trata de un anteojo astronómico
al que se ha añadido una lente denominada inversora. La imagen
del infinito se forma en el plano focal imagen del objetivo. Esta
imagen
se proyecta a través de la lente inversora, formándose una
nueva imagen intermedia. El plano de formación de esta imagen es
coincidente
con el plano focal objeto del ocular, y por lo tanto los rayos salen
paralelos
del sistema. Puesto que el aumento de la proyección a través
de la lente inversora es negativo, el aumento total es positivo.
Figura 1.32:Anteojo
terrestre
![\includegraphics[width=\textwidth]{teleterr.eps}](img139.gif) |
Se puede demostrar que el anteojo terrestre
tiene un aumento visual que es
igual a
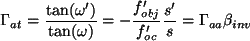 . . |
(1.19) |
El aumento visual en este caso es igual al aumento visual
correspondiente
al anteojo astronómico 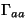 que podríamos construir sin inversora, multiplicado por el aumento
lateral de la proyección de la imagen intermedia a través de
la lente inversora. Puesto que ambos aumentos parciales son negativos,
el
aumento total es positivo. En este instrumento, el objetivo actúa
como pupila de entrada. La posición de la imagen de esta a través
de la inversora y el ocular, indica donde se debe poner el ojo. El
diafragma
de campo en este instrumento se encuentra situado equivalentemente en
el
plano focal imagen del objetivo o en plano focal objeto del ocular,
aunque
normalmente se coloca en el segundo.
que podríamos construir sin inversora, multiplicado por el aumento
lateral de la proyección de la imagen intermedia a través de
la lente inversora. Puesto que ambos aumentos parciales son negativos,
el
aumento total es positivo. En este instrumento, el objetivo actúa
como pupila de entrada. La posición de la imagen de esta a través
de la inversora y el ocular, indica donde se debe poner el ojo. El
diafragma
de campo en este instrumento se encuentra situado equivalentemente en
el
plano focal imagen del objetivo o en plano focal objeto del ocular,
aunque
normalmente se coloca en el segundo.
1.3.5
Telescopios de espejos
Basándose en el telescopio astronómico, se
pueden diseñar
telescopios en los cuales el objetivo es un sistema de espejos en vez
de
lentes. Estos sistemas pueden presentar valores de 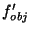 muy grandes, lo que supone grandes aberturas, y
por lo tanto el instrumento es muy luminoso. Además, los espejos no
presentan
aberración cromática. Los grandes telescopios presentan arquitecturas
de este tipo. La figura 1.33
muestra un ejemplo
de telescopio de espejos: al determinar la posición del plano principal
objeto obtenemos que la focal del objetivo es muy grande, lo que supone
un
valor del aumento muy elevado. muy grandes, lo que supone grandes aberturas, y
por lo tanto el instrumento es muy luminoso. Además, los espejos no
presentan
aberración cromática. Los grandes telescopios presentan arquitecturas
de este tipo. La figura 1.33
muestra un ejemplo
de telescopio de espejos: al determinar la posición del plano principal
objeto obtenemos que la focal del objetivo es muy grande, lo que supone
un
valor del aumento muy elevado.
Figura 1.33:Telescopio
de Cassegrain
![\includegraphics[width=\textwidth]{37_11.eps}](img142.gif) |
|

