JOptics

Català

Castellano

English

JOptics Curso de Óptica


JOptics
Inicio (Aplicaciones)
Presentación
Apuntes de Teoría
Ejercicios
Guía para Secundaria
Recursos
Actividades del grupo
Requisitos Técnicos
Novedades
Créditos

	Para más información: Grupo de Innovación Docente en Óptica Física y Fotónica Departamento de Física Aplicada y Óptica Universitat de Barcelona Martí i Franquès 1 08028 Barcelona Teléfono: 93 402 11 43 Fax: 93 403 92 19 optics at ub.edu

Índice

4.3 Estudio de casos particulares en aproximación de Fraunhofer

Subsecciones

4.3.1 Onda plana a través de un objeto rectangular

Para calcular la difracción de Fraunhofer de un objeto utilizaremos la siguiente ecuación

$\begin{displaymath} U(x,y,z)=\frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+y^2)}{\cal TF}_{\lambda z}[\psi(x_0,y_0)] \vspace{5mm} \end{displaymath}$ .

(4.31)

Supongamos que el objeto es iluminado por una onda plana $Ae^{ikz}$ . En , la onda plana es A. Escribiremos la transformada de Fourier de una función como , donde son las frecuencias espaciales. Es necesario recordar que la Transformada de Fourier de una abertura rectangular de dimensiones $l_x \times l_y$ vale

$\begin{displaymath} {\cal TF}\left [ rect(\frac{x}{l_x}) rect(\frac{y}{l_y}) \right ] = l_x l_y sinc (l_x u) sinc(l_y v) \vspace{5mm} \end{displaymath}$ ;

(4.32)

y, por lo tanto, el campo eléctrico escalar a distancia mucho mayor que o se escribe

$\displaystyle U(x,y,z)=A \frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+y^2)}{\cal TF}_{\lambda z}[rect(\frac{x}{l_x}) rect(\frac{y}{l_y})] =$	(4.33)
$\displaystyle = A \frac{e^{ikz}}{i \lambda z} l_x l_y e^{\frac{ik}{2z}(x^2+y^2)} sinc(\frac{l_x x}{\lambda z}) sinc(\frac{l_y y}{\lambda z}) \vspace{5 mm}$ ,

donde se han sustituido las variables (u,v) por $\frac{x}{\lambda z}$ y $\frac{y}{\lambda z}$ . La intensidad grabada por un detector será el módulo al cuadrado de la expresión anterior,

$\begin{displaymath} I(x,y,z) = A^2 \frac{l_x^2 l_y^2}{\lambda^2 z^2} sinc^2(\frac{l_x x}{\lambda z}) sinc^2(\frac{l_y y}{\lambda z}) \vspace{5mm} \end{displaymath}$ .

(4.34)

**Figura 4.4:** Difracción de Fraunhofer de un rectángulo cuyo lado vertical es menor que el horizontal
$\includegraphics[width=8cm,height=8cm]{difr2.ps}$

**Figura 4.5:** Perfil de la función que describe la intensidad de la difracción de Fraunhofer de un rectángulo
$\includegraphics[width=10cm,height=10cm]{sinc.eps}$

4.3.2 Onda plana a través de un objeto circular

La fórmula para calcular la difracción de Fraunhofer se puede escribir en coordenadas polares cuando el objeto tiene simetría circular, $\psi(r,\theta) = \psi(r)$ :

$\begin{displaymath} U(x,y,z)=\frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}r^2}{\cal TF}_{\lambda z}[\psi(r_0)] \vspace{5 mm} \end{displaymath}$ .

(4.35)

La transformada de Fourier de una función con simetría circular es

$\begin{displaymath} \int_{-\infty}^\infty f(x,y) e^{-2\pi i(xu+yv)}\;dx\;dy = \i... ... \cos(\theta_0 - \theta)} r_0 dr_0 = F(r,\theta) \vspace{5 mm} \end{displaymath}$ ,

(4.36)

donde se ha aplicado el cambio $x=r_0 \cos \theta_0$ , $y=r_0 \sin \theta_0$ y $u=r \cos \theta$ , $v=r \sin \theta$ . Utilizando la igualdad,

$\begin{displaymath} J_0(a)=\frac{1}{2\pi} \int_0^{2\pi} e^{-ia\cos(\theta-\phi)} d\theta \vspace{5 mm} \end{displaymath}$

(4.37)

se obtiene que

$\begin{displaymath} F(r) = 2 \pi \int_0^\infty f(r_0) J_0(2\pi r r_0) r_0\;dr_0 \vspace{5 mm} \end{displaymath}$ .

(4.38)

Para calcular la difracción de Fraunhofer cuando una onda plana $Ae^{ikz}$ atraviesa una abertura circular de radio , $circ(\frac{r}{R})$ en , tenemos que calcular la integral anterior. (f(r₀)=1 entre 0 i R). Aplicando ahora la relación

$\begin{displaymath}\frac{R}{a}J_1(aR) = \int_0^R J_0(ar) r\;dr, \vspace{5 mm} \end{displaymath}$

(4.39)

se puede demostrar que

$\begin{displaymath} {\cal TF}\left [circ(\frac{r_0}{R})\right] = R \frac{J_1(2\pi R r)}{r} \vspace{5 mm} \end{displaymath}$ ;

(4.40)

y, por lo tanto, el campo eléctrico escalar vale

$\displaystyle U(x,y,z)=A \frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+y^2)}{\cal TF}_{\lambda z}[circ(\frac{r_0}{R})] =$	(4.41)
$\displaystyle A \frac{e^{ikz}}{i \lambda z} R e^{\frac{ik}{2z}(r^2)} \frac{J_1(... ...-i A R e^{ikz} e^{\frac{ik}{2z}(r^2)} \frac{J_1(\frac{2\pi R r}{\lambda z})}{r}$ ,

mientras que la intensidad,

$\begin{displaymath} I(r) = A^2 \frac{R^2}{r^2} J_1^2(\frac{2\pi Rr}{\lambda z}) \vspace{5 mm} \end{displaymath}$ .

(4.42)

Se conoce como el radio del disco de Airy al radio del primero mínimo de la función anterior. La función $\frac{J_1(\pi x)}{\pi x}$ se anula en y, por lo tanto,

$\begin{displaymath} r_A=1.22 \frac{\lambda z}{2R} \vspace{5 mm} \end{displaymath}$ .

(4.43)

**Figura 4.6:**Difracción de Fraunhofer de un círculo
$\includegraphics[width=8cm,height=8cm]{difrac.ps}$

**Figura 4.7:** Perfil de la función que describe la intensidad de la difracción de Fraunhofer de un círculo. El primer cero de la función está en r=1.22
$\includegraphics[width=10cm]{j1.eps}$

4.3.3 Onda plana a través de una estructura periódica unidimensional

Sea un objeto de transmitancia repetido periódicamente N veces, con periodo 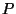. La función matemática que modeliza este objeto se escribe

$\begin{displaymath} \psi(x,y) = \sum_{m=0}^{N-1} f(x-mP) \vspace{5mm} \end{displaymath}$ .

(4.44)

La transformada de Fourier a escala $\lambda z$ de la expresión anterior es

$\begin{displaymath} TF_{\lambda z} [\psi(x_0,y_0)] =F(\frac{x} {\lambda z}, \fra... ...exp(-\frac{2 \pi i x(n-1)P}{\lambda z}) \right ) \vspace{5mm} \end{displaymath}$ ;

(4.45)

y, por lo tanto, cuando una onda plana atraviesa este objeto, el campo eléctrico escalar es

$\begin{displaymath} U(x,y,z)=A \frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+... ..._{m=0}^{N-1} \exp(-\frac{2 \pi i xmP}{\lambda z}) \vspace{5mm} \end{displaymath}$ .

(4.46)

Los términos de la suma de la ecuación anterior siguen una progresión geométrica cuya razón es $r=\exp(-\frac{2 \pi i xmP}{\lambda z})$ . Puesto que se verifica

$\begin{displaymath} 1+r+r^2+ r^3 + \ldots + r^{N-1} = \frac{1-r^N}{1-r} \vspace{5mm} \end{displaymath}$ ,

(4.47)

entonces

$\begin{displaymath} U(x,y,z)=A \frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+... ...ambda z})}{1-\exp(-\frac{2 \pi i xP}{\lambda z})} \vspace{5mm} \end{displaymath}$ .

(4.48)

Puede comprobarse que

$\begin{displaymath} \left \vert \frac{1-\exp(-\frac{2 \pi i x(N-1)P}{\lambda z})... ...(\pi NPx /\lambda z)}{\sin^2(\pi Px /\lambda z)} \vspace{5mm} \end{displaymath}$ ;

(4.49)

la intensidad se escribe como

$\begin{displaymath} I(x,y,z) \propto A^2 \left \vert F(\frac{x}{\lambda z}, \fra... ...mbda z)}{\sin^2(\pi Px /\lambda z)} \right \vert \vspace{5mm} \end{displaymath}$ .

(4.50)

Algunos comentarios adicionales:

La expresión de la intensidad nos indica que la distribución de luz que detectaremos es el producto de la difracción del objeto por un término interferencial.
El numerador del término de interferencial se anula cuando se verifica que $N P x = n \lambda z$ donde es un natural. Por lo tanto, cuando $x=n \lambda z /N P$ , la intensidad se anula (pasa por un mínimo). Entre dos mínimos tenemos un máximo secundario (ver figura 4.8).
El denominador del término de interferencial se anula cuando se verifica que $P x = n \lambda z$ donde es un natural. Es fácil comprobar que, en estos puntos donde el denominador se anula, también lo hace el numerador. Deshaciendo la indeterminación puede comprobarse que el término interferencial vale (máximo principal) (ver figura 4.8).
Si el número de franjas es N, entre dos máximos principales tenemos mínimos y máximos secundarios.
Si , el término interferencial se escribe

$\begin{displaymath} I(x,y,z) \propto 4 \cos^2(\frac{\pi P x}{\lambda z}) \end{displaymath}$ , (4.51)

que corresponde a la intensidad de las interferencias generadas por dos fuentes puntuales de luz (experimento de Young).
Por ejemplo, la intensidad de la difracción de Fraunhofer que generan dos objetos cuadrados de lado separados una distancia se escribe

$\begin{displaymath} I(x,y,z) \propto4 A^2 {\textrm sinc}(\frac{lx}{\lambda z}) {... ... sinc}(\frac{ly}{\lambda z}) \cos^2(\frac{\pi P x}{\lambda z}) \end{displaymath}$ . (4.52)

**Figura 4.8:** Perfil de la función que describe la intensidad de las interferencias para N=4
$\includegraphics[width=10cm, height=8cm]{no.eps}$

Índice