JOptics

**Figura 4.3:** Difracción de Fresnel
$\includegraphics[width=\textwidth]{difresnel.eps}$

A partir de ahora fijaremos unos ejes coordenados

en la pantalla que contiene la abertura. El eje

es el eje normal al plano de la abertura, que consideraremos en

. Los puntos del plano normal al eje

que contiene el punto de observación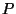

tendrán coordenadas

. La distancia de observación

será mucho mayor que las distancias transversales involucradas y, por lo tanto, podemos considerar que el factor de oblicuidad es cercano a la unidad. Escribiendo la fórmula de Fresnel-Kirchhoff en coordenadas cartesianas tenemos

$\displaystyle U(P)$	$\textstyle =$	$\displaystyle \frac{1}{i \lambda} \int_\Sigma U(\Sigma) \frac{\exp(ikr)}{r} \approx$	(4.22)
	$\textstyle \approx$	$\displaystyle \frac{1}{i\lambda} \int_\Sigma U(x_0,y_0,0) \frac{\exp(ik\sqrt{((... ...)^2+(y-y_0)^2+z^2})}{\sqrt{((x-x_0)^2+(y-y_0)^2+z^2})} dx_0 \;dy_0 \vspace{5mm}$ .	(4.22)

$\begin{displaymath} r=\sqrt{(x-x_0)^2+(y-y_0)^2+z^2} = z \sqrt{1 + \frac{(x-x_0)^2}{z^2} + \frac{(y-y_0)^2}{z^2}} \vspace{5mm} \end{displaymath}$ .

(4.23)

Si se verifica que $(x-x_0)^2+(y-y_0)^2 \ll z^2$ , se puede aproximar

por

en el denominador. Sin embargo, el término de la exponencial compleja presente en la integral varía muy rápidamente (debido al factor $2\pi / \lambda$ ), y por lo tanto, un pequeño error en la evaluación de

, puede suponer un error muy grande en la estimación del ángulo. Para simplificar correctamente la expresión del interior de la integral de difracción, desarrollamos

en serie de Taylor,

$\begin{displaymath} r= z \sqrt{1 + \frac{(x-x_0)^2}{z^2} + \frac{(y-y_0)^2}{z^2... ...x_0)^2}{2z^2} + \frac{(y-y_0)^2}{2z^2} \right ] \vspace{5mm} \end{displaymath}$ .

(4.24)

Esto equivale a aproximar una superficie esférica por una superficie parabólica. La fórmula de difracción toma ahora la forma siguiente (fórmula de difracción de Fresnel):

$\begin{displaymath} U(x,y,z)=\frac{\exp(ikz)}{i \lambda z} \int_\Sigma U(x_0,y_... ...frac{ik}{2z}((x-x_0)^2+(y-y_0)^2)) dx_0 \;dy_0 \vspace{5mm} \end{displaymath}$ .

(4.25)

Los límites de integración corresponden a abertura $\Sigma$ . Puesto que el campo eléctrico es cero a fuera de la abertura, podemos extender los límites de integración de $-\infty$ a $+\infty$ , haciendo que

$\begin{displaymath} \psi(x,y)=U(x,y,0)G(x,y) \;\textrm{,} \vspace{5mm} \end{displaymath}$

(4.26)

$\begin{displaymath} U(x,y,z)=\frac{\exp(ikz)}{i \lambda z} \int_{-\infty}^\inft... ...frac{ik}{2z}((x-x_0)^2+(y-y_0)^2)) dx_0 \;dy_0 \vspace{5mm} \end{displaymath}$ .

(4.27)

$\displaystyle U(x,y,z)$	$\textstyle =$	$\displaystyle \frac{e^{ikz}}{i \lambda z} \exp(\frac{ik}{2z}(x^2+y^2)) \int_{-\... ..._0) e^{\frac{ik}{2z}(x_0^2+y_0^2)} e^{-\frac{ik}{z}(xx_0 + yy_0)} dx_0 \;dy_0 =$	(4.28)
	$\textstyle =$	$\displaystyle \frac{e^{ikz}}{i \lambda z} \exp(\frac{ik}{2z}(x^2+y^2)) \int_{-\... ...^2)} e^{ -2 \pi y(\frac{x}{\lambda z}x_0 + \frac{i}{\lambda z}y_0)} dx_0 \;dy_0$ .	(4.28)

Cuando la distancia de observación

es muy grande, la exponencial $\exp(\frac{ik}{2z}(x_0^2+y_0^2))$ en el interior de la integral tiende a la unidad. Es necesario tener en cuenta que las dimensiones de la abertura $\Sigma$ serán pequeñas en comparación con

, aunque esto no es necesario que se verifique en el plano de observación. Por esta razón el término exponencial cuadrático de fuera de la integral no desaparece. Cuando se verifican estas condiciones, decimos que trabajamos en condiciones de difracción de Fraunhofer. La integral de difracción se escribe ahora

$\displaystyle U(x,y,z)$	$\textstyle =$	$\displaystyle \frac{e^{ikz}}{i \lambda z} e^{\frac{ik}{2z}(x^2+y^2)} \int_{-\in... ... \exp( -2 \pi i(\frac{x}{\lambda z}x_0 + \frac{y}{\lambda z}y_0)) dx_0 \;dy_0 =$	(4.29)
	$\textstyle =$	$\displaystyle \frac{e^{ikz}}{i \lambda z} \exp(\frac{ik}{2z}(x^2+y^2)){\cal TF}_{\lambda z}[\psi(x_0,y_0)] \vspace{5mm}$ ,	(4.29)

donde ${\cal TF}$ representa el operador transformada de Fourier. La intensidad que captaría un detector en estas condiciones es

$\begin{displaymath} I(x,y,z)\propto \vert{\cal TF}_{\lambda z}[\psi(x_0,y_0)] \vert^2 \vspace{5mm} \end{displaymath}$ .

(4.30)

Es decir, en condiciones de difracción de Fraunhofer, la distribución de intensidad es proporcional a la transformada de Fourier a escala $\lambda z$ del campo eléctrico en el plano que contiene la abertura.