|
4.1 Teoría escalar
Subsecciones
4.1.1
Introducción a la Teoría Escalar de la Difracción
Sommerfeld definió la difracción como la
propagación no rectilínea de la luz que no se puede
interpretar a partir de las leyes de la reflexión y de la
refracción. Grimaldi, en el siglo XVII, fue el primero que
observó fenómenos difractivos: al hacer pasar un haz de
luz a través de una abertura practicada sobre una pantalla
observó que, al proyectar el haz sobre otra pantalla, el paso de
la zona iluminada a la zona de sombra no era abrupto (como indica la
propagación rectilínea). Años después,
Fresnel realizó el primer intento serio de explicar los
fenómenos de difracción (1818), basándose en unas
modificaciones arbitrarias del principio de Huygens. En 1882, Kirchhoff
propuso la explicación de los fenómenos de
difracción en términos de la teoría escalar. Su
teoría tiene inconvenientes formales de orden matemático
que fueron solucionados por Sommerfeld en 1894, introduciendo algunas
modificaciones en la teoría anterior.
La teoría escalar es suficientemente rigurosa
para explicar
la mayor parte de los resultados experimentales macroscópicos.
Pese a que se trata de una simplificación que no tiene en cuenta
el carácter vectorial de los campos electromagnéticos, la
teoría escalar funciona con éxito cuando las aberturas
son más grandes que la longitud de onda de la luz y cuando las
distancias de observación son suficientemente grandes. En estas
condiciones, la polarización del campo electromagnético
no es una información relevante y, por lo tanto, se puede
prescindir del formalismo vectorial.
4.1.2 Ondas escalares.
El teorema de Green
Una onda escalar perfectamente monocromática
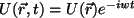 que
se propaga en el vacío, verifica la ecuación de ondas: que
se propaga en el vacío, verifica la ecuación de ondas:
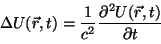 . . |
(4.1) |
En consecuencia, la amplitud compleja (parte
espacial) 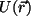 verifica la
ecuación
de Helmholtz: verifica la
ecuación
de Helmholtz:
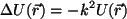 , , |
(4.2) |
donde r es el
vector de
posición,  es el
número de onda, es el
número de onda, 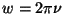 ,
y ,
y  . .
La formulación de la teoría escalar de la
difracción se basa en el uso del teorema de Green:
Sean 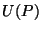 y y 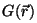 dos funciones que toman
valores complejos, continuas y con primera y segunda derivadas
continuas en el interior de un recinto dos funciones que toman
valores complejos, continuas y con primera y segunda derivadas
continuas en el interior de un recinto  cerrado por la superficie cerrado por la superficie 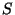 . En estas condiciones se verifica: . En estas condiciones se verifica:
![\begin{displaymath}
\int_V \left [ G \Delta U - U \Delta G \right ] dv = \int_S ...
...n} - U \frac{\partial G}{\partial n} \right ] ds
\vspace{5mm}
\end{displaymath}](img668.gif) . . |
(4.3) |
Figura 4.1:
Teorema de Green.
Geometría
![\includegraphics[width=10cm]{patata.eps}](img669.gif) |
En el problema que abordaremos, 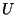 será la parte espacial de la ecuación de ondas, y
será la parte espacial de la ecuación de ondas, y 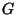 , una función auxiliar
denominada función de Green. La elección de
ésta, solamente está condicionada por el propio teorema de Green; no
obstante, es necesario escogerla de forma que el
problema se pueda abordar con el mínimo de complicaciones
matemáticas posible. La notación , una función auxiliar
denominada función de Green. La elección de
ésta, solamente está condicionada por el propio teorema de Green; no
obstante, es necesario escogerla de forma que el
problema se pueda abordar con el mínimo de complicaciones
matemáticas posible. La notación
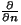 hace
referencia a la derivada de hace
referencia a la derivada de 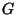 o o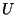 según la dirección
normal de la superficie según la dirección
normal de la superficie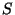 . A
partir
de ahora, no se tendrá en cuenta la parte temporal de la
onda. Sea . A
partir
de ahora, no se tendrá en cuenta la parte temporal de la
onda. Sea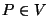 , el punto donde
haremos la observación del campo. Definimos una posible
función de Green como , el punto donde
haremos la observación del campo. Definimos una posible
función de Green como
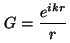 . . |
(4.4) |
En el punto 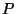 ( (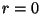 )
esta función no
está definida. Para evitar la discontinuidad en )
esta función no
está definida. Para evitar la discontinuidad en 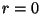 , se excluye el punto , se excluye el punto 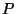 del recinto del recinto  definiendo una superficie esférica definiendo una superficie esférica 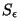 alrededor de alrededor de 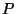 con un radio con un radio  infinitesimal. Así, la nueva superficie
de integración infinitesimal. Así, la nueva superficie
de integración 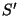 será
será 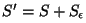 y el nuevo volumen y el nuevo volumen 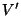 , , 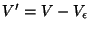 ; ; 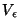 es el volumen definido por es el volumen definido por 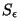 . La función . La función 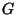 es una onda esférica de
amplitud unidad y, por lo tanto, verifica también la
ecuación de Helmholtz: es una onda esférica de
amplitud unidad y, por lo tanto, verifica también la
ecuación de Helmholtz:
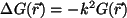 .
Aplicando el teorema de Green al nuevo recinto de integración
V' obtenemos .
Aplicando el teorema de Green al nuevo recinto de integración
V' obtenemos
![\begin{displaymath}
\int_{V'} \left [ G \Delta U - U \Delta G \right ] dv = - \int_{V'}\left [
k^2 G U - k^2 U G \right ] dv = 0
\vspace{5mm}
\end{displaymath}](img683.gif) ; ; |
(4.5) |
entoces
![\begin{displaymath}
\int_{S'} \left [ G \frac{\partial U}{\partial n} - U \frac{\partial
G}{\partial n} \right ] ds =0
\vspace{5mm}
\end{displaymath}](img684.gif) , , |
(4.6) |
y como 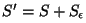 , tenemos que , tenemos que
![\begin{displaymath}
-\int_{S_\epsilon} \left [ G \frac{\partial U}{\partial n} -...
...l
U}{\partial n} - U \frac{\partial G}{\partial n} \right ] ds
\end{displaymath}](img685.gif) . . |
(4.7) |
4.1.3 Teorema integral
de Helmholtz-Kirchhoff
La evaluación de la integral definida sobre 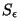 es sencilla. Se trata de
calcular el
límite siguiente, es sencilla. Se trata de
calcular el
límite siguiente,
![\begin{displaymath}
\lim_{\epsilon \rightarrow 0} \int_{S_\epsilon} \left [ G \...
... n} - U \frac{\partial G}{\partial n} \right ] ds
\vspace{5mm}
\end{displaymath}](img686.gif) . . |
(4.8) |
Al ser 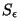 es una
superficie esférica, las derivadas normales de la
ecuación anterior pasan a ser derivadas en la dirección
radial es una
superficie esférica, las derivadas normales de la
ecuación anterior pasan a ser derivadas en la dirección
radial  . La derivada
normal en la superficie . La derivada
normal en la superficie 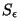 apunta hacia
apunta hacia 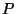 y, por lo
tanto, y, por lo
tanto,
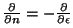 .
Puesto que la función .
Puesto que la función 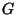 sobre la superficie
sobre la superficie 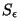 se
puede escribir como
se
puede escribir como 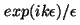 , la derivada
es , la derivada
es
![\begin{displaymath}
\frac{\partial G}{\partial n} = \left[ \frac{1}{\epsilon} -
ik\right]\frac{e^{ik\epsilon}}{\epsilon}
\vspace{5mm}
\end{displaymath}](img689.gif) . . |
(4.9) |
El diferencial de superficie es
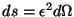 , donde , donde 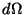 es
el diferencial de
ángulo sólido. Substituyendo en la integral, es
el diferencial de
ángulo sólido. Substituyendo en la integral,
![\begin{displaymath}
\lim_{\epsilon \rightarrow 0} \int_{S_\epsilon} \left [ G \f...
...k\epsilon}}{\epsilon} \right ] \epsilon^2 d\Omega
\vspace{5mm}
\end{displaymath}](img692.gif) . . |
(4.10) |
Las funciones y las derivadas presentes en la integral están
acotadas y, por lo tanto, de los tres términos contenidos en
ella, únicamente el segundo será diferente de cero.
Considerando, además, la continuidad de 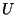 , ,
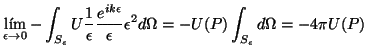 ; ; |
(4.11) |
la ecuación 4.7 se
escribirá
![\begin{displaymath}
U(P) = \frac{1}{4 \pi} \int_S \left [ G \frac{\partial U}{\p...
...ial n} \left
[\frac{e^{ikr}}{r}\right] \right] ds
\vspace{5mm}
\end{displaymath}](img694.gif) , , |
(4.12) |
resultado que se conoce como el teorema integral de
Helmholtz-Kirchhoff.
4.1.4 Aplicación
del teorema de Helmholtz-Kirchhoff a la difracción
En esta sección, se aplica el teorema
integral de
Helmholtz-Kirchhoff al problema de la difracción de una onda
escalar a través de una abertura contenida en una superficie
plana. Consideramos la superficie 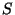 que rodea el punto de observación
que rodea el punto de observación 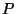 . La tomaremos subdividida en dos secciones . La tomaremos subdividida en dos secciones 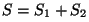 : :  corresponde al plano que contiene la abertura corresponde al plano que contiene la abertura  y y  es superficie esférica centrada en es superficie esférica centrada en 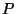 y de radio suficientemente grande.
Lo primero que debe hacerse es evaluar la integral 4.12 en la superficie y de radio suficientemente grande.
Lo primero que debe hacerse es evaluar la integral 4.12 en la superficie  . Al estar trabajando con iluminación
monocromática, y por lo tanto, de longitud de coherencia
infinita, una vez la onda se haya propagado a velocidad . Al estar trabajando con iluminación
monocromática, y por lo tanto, de longitud de coherencia
infinita, una vez la onda se haya propagado a velocidad  hasta hasta  , la contribución de la integral sobre , la contribución de la integral sobre  puede no ser despreciable. Para
aclarar este aspecto, calculamos el límite siguiente, puede no ser despreciable. Para
aclarar este aspecto, calculamos el límite siguiente,
![\begin{displaymath}
U(P) = \lim_{R\rightarrow \infty} \frac{1}{4 \pi} \int_{S_2}...
... n} - U \frac{\partial G}{\partial n} \right ] ds
\vspace{5mm}
\end{displaymath}](img697.gif) |
(4.13) |
La derivada en la dirección normal (radial)
de 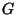 sobre sobre  vale vale
![\begin{displaymath}
\frac{\partial G}{\partial n} = \left[ \frac{1}{R} -
ik\right]\frac{e^{ikr}}{r} \approx ikG
\vspace{5mm}
\end{displaymath}](img698.gif) |
(4.14) |
si 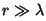 .
Por lo
tanto, la integral anterior vale .
Por lo
tanto, la integral anterior vale
![\begin{displaymath}
U(P) = \lim_{r \rightarrow \infty} \frac{1}{4 \pi} \int_{S_2...
...artial U}{\partial n} - ikU \right ] r^2 d\Omega
\vspace{5mm}
\end{displaymath}](img700.gif) , , |
(4.15) |
donde 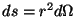 . Esta
integral tiende a cero si se
verifica . Esta
integral tiende a cero si se
verifica
![\begin{displaymath}
\lim_{r \rightarrow \infty} \left [
\frac{\partial U}{\partial n} - ikU \right ] = 0
\vspace{5mm}
\end{displaymath}](img702.gif) . . |
(4.16) |
Esta condición es cierta si 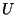 es una onda esférica ( es una onda esférica (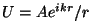 ). Dado que una onda cualquiera puede
ser expresada en términos de una combinación lineal de
ondas esféricas, en la práctica, este resultado se
verifica siempre. Por lo tanto, la contribución a ). Dado que una onda cualquiera puede
ser expresada en términos de una combinación lineal de
ondas esféricas, en la práctica, este resultado se
verifica siempre. Por lo tanto, la contribución a 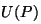 de la integral sobre de la integral sobre  puede ser despreciada. puede ser despreciada.
4.1.4.1 Condiciones de
contorno de Kirchhoff
Evaluemos ahora la integral sobre  .
Para ello, Kirchhoff impuso las siguientes condiciones para poder
realizar el cálculo: .
Para ello, Kirchhoff impuso las siguientes condiciones para poder
realizar el cálculo:
- El campo
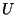 y su
derivada normal toman los mismos valores en la abertura y su
derivada normal toman los mismos valores en la abertura  , en presencia o no de la
superficie , en presencia o no de la
superficie  . .
- Sobre la superficie
 y fuera de
y fuera de  , , 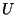 y su derivada normal valen cero. Esta
condición permite realizar la integral extendida
sólo a la geometría de y su derivada normal valen cero. Esta
condición permite realizar la integral extendida
sólo a la geometría de  . .
Figura 4.2:
Geometría.
Fórmula de Fresnel-Kirchhoff
![\includegraphics[width=12cm]{kirchhoff.eps}](img705.gif) |
4.1.4.2 Fórmula de
Fresnel-Kirchhoff
Para acabar, consideremos ahora la forma en
que se ilumina la abertura.
Concentrémonos en el caso en que la abertura está
iluminada por una onda esférica que proviene de un punto 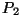 : : 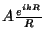 . Las derivadas
normales a . Las derivadas
normales a  de de  y y  valen
valen
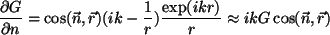 |
(4.17) |
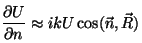 , , |
(4.18) |
donde
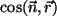 y y
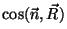 son los cosenos
de los ángulos formados por el vector normal a son los cosenos
de los ángulos formados por el vector normal a  y los vectores posición y los vectores posición  y y 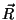 respectivamente. Por lo tanto la integral de
difracción en este caso es
respectivamente. Por lo tanto la integral de
difracción en este caso es
![\begin{displaymath}
U(P) = \frac{A}{2i \lambda} \int_{\Sigma} \frac{\exp(ik(r+R)...
...{n},\vec{r}) - \cos(\vec{n},\vec{R}) \right ] ds
\vspace{5mm}
\end{displaymath}](img713.gif) |
(4.19) |
conocida como la Fórmula de
Fresnel-Kirchhoff. Esta
fórmula nos da la expresión del campo escalar difractado
a través de una abertura cualquiera iluminada por una onda
esférica. Esta fórmula es simétrica respecto la
fuente o el punto de observación (teorema de reciprocidad).
4.1.4.3 Consideraciones
finales sobre la Fórmula
de Fresnel-Kirchhoff
- Si la abertura es pequeña frente a las distancias
 y y  ,
los factores ,
los factores 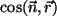 y y
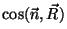 son
prácticamente constantes. Se denomina factor de oblicuidad
a la semidiferencia son
prácticamente constantes. Se denomina factor de oblicuidad
a la semidiferencia
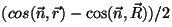
- Si la onda que ilumina la abertura no es esférica, es
posible describir cualquier campo en términos de ondas
esféricas, pudiéndose aplicar la fórmula deducida.
- Para ángulos pequeños (ie., distancias axiales
mucho mayores que las dimensiones de la abertura), el factor de
oblicuidad se hace próximo a la unidad, ya que
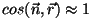 y
y 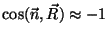 . .
- La expresión 4.19
se ha
deducido utilizando una onda esférica
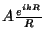 para iluminar la
abertura. Si la fuente de luz está en el infinito, la
abertura se ilumina con una onda plana: para iluminar la
abertura. Si la fuente de luz está en el infinito, la
abertura se ilumina con una onda plana:
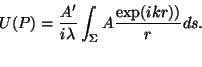 |
(4.20) |
- Si el sistema se ilumina con una onda cualquiera, cuya
amplitud
compleja en el plano de la abertura
 es es 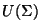 ,
la expresión puede generalizarse a ,
la expresión puede generalizarse a
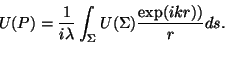 |
(4.21) |
|

