| |
3.2 Interferencias
de Young
Subsecciones
3.2.1 Descripción
del experimento
Consideremos el siguiente experimento: dos
emisores puntuales  y y  , coherentes entre sí, emiten ondas
esféricas
con igual frecuencia y polarización: , coherentes entre sí, emiten ondas
esféricas
con igual frecuencia y polarización:  y y  . Sea . Sea  la separación entre las dos fuentes.
Sea la separación entre las dos fuentes.
Sea  el plano que contiene las
dos fuentes. Consideramos un punto de observación el plano que contiene las
dos fuentes. Consideramos un punto de observación 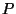 situado en situado en  .
Supongamos, sin perder generalidad, que el índice
del medio es .
Supongamos, sin perder generalidad, que el índice
del medio es  . .
Figura 3.5:
Interferencia de
dos ondas esféricas
![\includegraphics[width=14cm]{young.eps}](img516.gif) |
La intensidad que detectaremos en este punto
vendrá dada por la ecuación
3.6. Aunque
las distancias  y y  son diferentes, si son diferentes, si  es lo suficiente grande, las amplitudes de las ondas en el punto
es lo suficiente grande, las amplitudes de las ondas en el punto 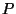 se pueden considerar iguales.
Intentemos
reescribir esta ecuación de forma que resulte más cómoda
de utilizar. El producto escalar se pueden considerar iguales.
Intentemos
reescribir esta ecuación de forma que resulte más cómoda
de utilizar. El producto escalar  no es
más que no es
más que  , donde , donde  y y  son las distancias entre la fuente son las distancias entre la fuente  y el punto de observación y el punto de observación 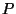 y la distancia entre la fuente y la distancia entre la fuente  y el punto de observación y el punto de observación 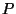 , respectivamente ( , respectivamente ( , por ejemplo, es la proyección del vector , por ejemplo, es la proyección del vector  según la dirección
fijada por la fuente según la dirección
fijada por la fuente  y el
punto y el
punto 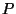 ). ).  es la diferencia de camino óptico
es la diferencia de camino óptico  , mientras que , mientras que  es la diferencia de fase. Las fuentes
es la diferencia de fase. Las fuentes  y y  se
encuentran
en los puntos se
encuentran
en los puntos  y
y  ,
respectivamente. Aplicando
la definición de distancia, tenemos que ,
respectivamente. Aplicando
la definición de distancia, tenemos que
 . . |
(3.7) |
En el experimento de Young se toma la distancia de observación  mucho más grande que la distancia
entre las fuentes mucho más grande que la distancia
entre las fuentes  . Si se
verifica
esta condición . Si se
verifica
esta condición  , entonces , entonces
 y la diferencia y la diferencia  puede escribirse puede escribirse
 . . |
(3.8) |
y, por lo tanto, la ecuación de la intensidad se escribirá
 . . |
(3.9) |
donde  es la amplitud en el plano
de observación, es la amplitud en el plano
de observación, 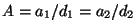
3.2.1.1 Análisis de la
figura de franjas de Young
- Una vez se ha fijado la geometría (
 , D ) y la
longitud
de onda, la intensidad que se registra es sólo una función
de la variable , D ) y la
longitud
de onda, la intensidad que se registra es sólo una función
de la variable  , ,  : por lo tanto, todos los puntos con la
misma intensidad estarán en rectas paralelas al eje : por lo tanto, todos los puntos con la
misma intensidad estarán en rectas paralelas al eje  . .
- El perfil de la intensidad según el eje
 varia como un coseno al cuadrado. Se trata de una
función que se hace máxima cuando varia como un coseno al cuadrado. Se trata de una
función que se hace máxima cuando  ( ( entero) y se hace cero cuando
entero) y se hace cero cuando  .
El máximo de orden .
El máximo de orden  se encontrará
en la posición se encontrará
en la posición
 , , |
(3.10) |
y la distancia entre dos máximos (interfranja) será
 . . |
(3.11) |
3.2.2 Dispositivos por obtener
franjas de Young
Existen algunos dispositivos experimentales
que permiten reproducir con facilidad
el experimento de Young. Se trata de conseguir que los dos emisores
puntuales
sean coherentes entre sí, es decir, que la fase aleatoria sea la misma
de manera que la diferencia de camino óptico  sea inferior a la longitud de coherencia sea inferior a la longitud de coherencia  . La única posibilidad para conseguir
esto es generar imágenes geométricas de un único foco
puntual de luz. . La única posibilidad para conseguir
esto es generar imágenes geométricas de un único foco
puntual de luz.
- Por ejemplo, el biprisma de Fresnel consiste en un
dispositivo como
el que se muestra en la figura 3.6. El ángulo
 es muy pequeño.
Sí colocamos una fuente de luz a distancia ` es muy pequeño.
Sí colocamos una fuente de luz a distancia ` ' del prisma, se puede demostrar que un observador
situado
al otro lado del prisma (a su derecha según la figura) verá
dos fuentes de luz (coherentes entre si) correspondientes a las
imágenes
geométricas de la fuente de luz a través del biprisma. ' del prisma, se puede demostrar que un observador
situado
al otro lado del prisma (a su derecha según la figura) verá
dos fuentes de luz (coherentes entre si) correspondientes a las
imágenes
geométricas de la fuente de luz a través del biprisma.
Figura 3.6:
Biprisma de
Fresnel
![\includegraphics[width=12cm]{biprisma.eps}](img542.gif) |
- Otra posibilidad es utilizar el espejo de Lloyd. Se trata
de colocar
una fuente delante de un espejo. La imagen virtual de la fuente a
través
del espejo actuará como segunda fuente coherente con la primera. Si
se trata de un espejo dieléctrico, el rayo reflejado tiene un cambio
de fase
 adicional. Se
puede comprobar
que esto implica que la figura de interferencias sea complementaria a
la
deducida anteriormente: allá donde había máximos tendremos
mínimos y viceversa. adicional. Se
puede comprobar
que esto implica que la figura de interferencias sea complementaria a
la
deducida anteriormente: allá donde había máximos tendremos
mínimos y viceversa.
Figura 3.7:Espejo
de Lloyd
|
|
3.2.3 Coherencia espacial
En el apartado anterior hemos considerado que
la fuente de luz original es
puntual. En cambio, las fuentes de luz reales tienen unas determinadas
dimensiones.
Definimos el contraste de las franjas (también denominadofactor
de visibilidad,  ) como el
cociente ) como el
cociente
 , , |
(3.12) |
donde  e e  son las intensidades máxima y mínima en
una distribución de interferencias. Para un experimento de Young
ideal, son las intensidades máxima y mínima en
una distribución de interferencias. Para un experimento de Young
ideal,  , por lo tanto,
el contraste
de las franjas será siempre óptimo, , por lo tanto,
el contraste
de las franjas será siempre óptimo,  . En cambio, si las amplitudes de las dos ondas que
interfieren
son diferentes, . En cambio, si las amplitudes de las dos ondas que
interfieren
son diferentes,  y, en
este caso,
y, en
este caso,  . Si no se
aprecian interferencias, . Si no se
aprecian interferencias,
 , entonces , entonces  . Si la fuente de luz que
ilumina el sistema no es puntual,
el factor de visibilidad también puede ser inferior a 1, incluso
verificándose
estrictamente las cuatro condiciones para obtener imágenes de
interferencias
estables. El fenómeno de la pérdida de contraste en las franjas
a consecuencia de las dimensiones de la fuente está relacionado con
el concepto de Coherencia espacial. El estudio de este
fenómeno
se hace considerando que cada punto de la fuente es un emisor puntual
que
genera su sistema de franjas de interferencia. Se puede demostrar que
cada
uno de estos emisores elementales genera un sistema de franjas con un
origen
diferente (posición del máximo . Si la fuente de luz que
ilumina el sistema no es puntual,
el factor de visibilidad también puede ser inferior a 1, incluso
verificándose
estrictamente las cuatro condiciones para obtener imágenes de
interferencias
estables. El fenómeno de la pérdida de contraste en las franjas
a consecuencia de las dimensiones de la fuente está relacionado con
el concepto de Coherencia espacial. El estudio de este
fenómeno
se hace considerando que cada punto de la fuente es un emisor puntual
que
genera su sistema de franjas de interferencia. Se puede demostrar que
cada
uno de estos emisores elementales genera un sistema de franjas con un
origen
diferente (posición del máximo  ).
La superposición de los diferentes términos ).
La superposición de los diferentes términos
 de la
ecuación 3.9, con
un pequeño desplazamiento entre
ellas, provoca la pérdida de contraste. de la
ecuación 3.9, con
un pequeño desplazamiento entre
ellas, provoca la pérdida de contraste.
|

