PRUEBAS PARA K MUESTRAS INDEPENDIENTES
En este apartado se presentan dos pruebas que permiten contrastar si k >2 muestras aleatorias e independientes proceden de una misma población, es decir, si un factor que subdivide la población de origen incide de forma significativa sobre el valor central de la población. Estos contrastes son alternativas no paramétricas al análisis de la varianza cuando se incumple alguno de los supuestos básicos de dicho análisis. El único requisito para aplicar estos contrastes es que la variable esté medida al menos en una escala ordinal.
Este contraste permite decidir si puede aceptarse la hipótesis de que k muestras independientes proceden de la misma población o de poblaciones idénticas con la misma mediana. El único supuesto necesario es que las distribuciones subyacentes de las variables sean continuas y que éstas hayan sido medidas por lo menos en una escala ordinal.
Sean n1, n2 ... nk los tamaños de cada una de las muestras y n el total de observaciones. Para el cálculo del estadístico de prueba se ordenan las n observaciones de menor a mayor y se les asignan rangos desde 1 hasta n. A continuación se obtiene la suma de los rangos correspondientes a los elementos de cada muestra, Rj y se halla el rango promedio. Si la hipótesis nula es cierta, es de esperar que el rango promedio sea aproximadamente igual para las k muestras; cuando dichos promedios sean muy diferentes es un indicio de que H0 es falsa.
El estadístico de prueba es:
Si H0 es cierta y los tamaños muestrales son todos mayores que 5, el estadístico H se distribuye aproximadamente como chi-cuadrado con k-1 grados de libertad. La aproximación es tanto mejor cuanto mayor es el número de muestras y el tamaño de las mismas.
Cuando se producen empates, es decir, cuando varias observaciones de la misma o de distintas muestras son iguales y a todas se les asigna el mismo rango, es necesario dividir el valor de H por el siguiente factor de corrección:
En esta expresión g es el número de rangos que se repiten y ti es el número de veces que se repite el rango i-ésimo. El efecto del factor de corrección es elevar ligeramente el valor de H.
Mediante esta prueba se contrasta la hipótesis nula de que k muestras independientes de tamaños n1, n2 ... nk proceden de la misma población o de poblaciones con medianas iguales. Para este contraste se requiere que la variable sea medible por lo menos en una escala ordinal y es particularmente útil cuando por alguna razón (como, por ejemplo, por haberse establecido puntos de corte durante el proceso de obtención de los datos) se sabe que las muestras no pueden contener observaciones extremas.
Para hallar el valor del estadístico de prueba se ordenan las n observaciones (n1 + n2 +... +nk) de menor a mayor y se determina el valor de la mediana común, Me.. A continuación, cada una de las observaciones originales se asigna a una de dos categorías: a la categoría 1 si es superior a la mediana común o a la categoría 2 si es inferior o igual.
El número de observaciones de cada grupo asignadas a cada categoría se recoge en una tabla de contingencia como la siguiente:
Muestra Superiores a Me Inferiores a Me Inferior o iguales a Me |
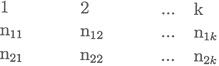 |
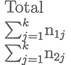 |
| Total | n |
El estadístico de prueba es:
Eij es la frecuencia esperada en la i-ésima fila de la j-ésima columna bajo el supuesto de que la hipótesis nula es cierta, calculada como producto de las frecuencias marginales dividido por n. Si la hipótesis nula es cierta el estadístico de prueba se distribuye aproximadamente como una chi-cuadrado con k - 1 grados de libertad. Se rechazará H0 si el valor del estadístico de prueba está en la región crítica.
Cuando aparecen frecuencias esperadas menores que 5 la aproximación de la distribución del estadístico de prueba mediante la chi-cuadrado no es buena y deberán agruparse muestras o aumentar el tamaño de las mismas para resolver el problema.
Para realizar estas pruebas la secuencia es:
Analizar
Pruebas no paramétricas
k muestras independientes
En el cuadro de diálogo se seleccionan en Contrastar variables la variable que recoge las puntuaciones de los grupos. En Variable de agrupación se indica la variable que determina los grupos, es decir, la variable que actúa como factor y se indica en Definir el rango los valores enteros para el máximo y el mínimo que se correspondan con las categorías mayor y menor de la variable de agrupación. Se activa la o las pruebas que se quieren realizar en el recuadro Tipo de prueba. Por defecto únicamente está activada la prueba H de Kruskal-Wallis.
EJEMPLO
Con los datos de la encuesta Enctrans.sav probar si los alumnos que utilizan habitualmente los transportes públicos (metro, bus, tren) valoran de forma significativamente distinta las características independencia (Inde) y rapidez (Rapi).
Se trata de contrastar la hipótesis nula de que la valoración asignada a la independencia y a la rapidez difieren significativamente en función del tipo de transporte público utilizado. Dado que las valoraciones de ambas características se miden en una escala ordinal y las muestras son independientes, el contraste más adecuado es la prueba H de Kruskal-Wallis.
Para realizar este contraste la secuencia es:
Estadística > Pruebas no paramétricas > k muestras independientes.
En el cuadro de diálogo se selecciona en Contrastar variables Independencia y Rapidez; en Variable de agrupación se indica el factor, es decir, la variable que induce los diferentes grupos, que en este caso es la variable Trans. Como únicamente interesa comparar la opinión de los usuarios del transporte público en el cuadro de diálogo que se abre con el botón Definir rango se indica como rango Mínimo 1 y como rango Máximo 3, ya que 1, 2 y 3 son las codificaciones asignadas a las modalidades metro, bus y tren respectivamente. Al aceptar se obtienen los siguientes resultados:
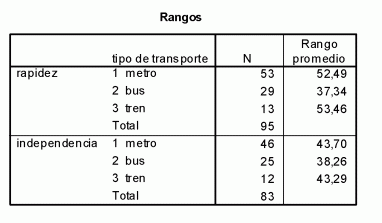

Por lo que se refiere a la variable Rapidez, el estadístico de prueba es 6,449 y por tanto se rechaza la hipótesis nula según la cual los tres grupos valoran igualmente esta característica. En el caso de la variable Independencia el valor del estadístico Chi-cuadrado es 0,891 y no se rechaza la hipótesis nula