PRUEBAS PARA K MUESTRAS DEPENDIENTES

Cuando las k muestras están relacionadas de forma que las características de los i-ésimos elementos de cada muestra son idénticas o lo más parecidas posible, las diferencias observadas entre las muestras serán atribuidas únicamente al efecto del factor diferenciador de los grupos. El contraste de la hipótesis de que las k muestras proceden de una misma población o de poblaciones con la misma tendencia central no puede realizarse mediante el análisis de la varianza, al incumplirse el supuesto, por lo menos, de independencia de las muestras. En este caso puede utilizarse alguna de las alternativas no paramétricas que se presentan a continuación.

PRUEBA DE FRIEDMAN

Esta prueba puede utilizarse en aquellas situaciones en las que se seleccionan n grupos de k elementos de forma que los elementos de cada grupo sean lo más parecidos posible entre sí, y a cada uno de los elementos del grupo se le aplica uno de entre k ''tratamientos'', o bien cuando a cada uno de los elementos de una muestra de tamaño n se le aplican los k ''tratamientos''.

La hipótesis nula que se contrasta es que las respuestas asociadas a cada uno de los ''tratamientos'' tienen la misma distribución de probabilidad o distribuciones con la misma mediana, frente a la hipótesis alternativa de que por lo menos la distribución de una de las respuestas difiere de las demás. Para poder utilizar esta prueba las respuestas deben ser variables contínuas y estar medidas por lo menos en una escala ordinal.

Los datos se disponen en una tabla en la que en cada fila se recogen las respuestas de los k elementos de cada grupo a los k tratamientos:

A las observaciones de cada fila se les asignan rangos de menor a mayor desde 1 hasta k; a continuación se suman los rangos correspondientes a cada columna, siendo RJ la suma correspondiente a la columna j-ésima. Si la hipótesis nula es cierta, la distribución de los rangos en cada fila se debe al azar, y es de esperar que la suma de los rangos correspondientes a cada columna sea aproximadamente igual a n(k + 1)/2. La prueba de Friedman determina si las RJ observadas difieren significativamente del valor esperado bajo la hipótesis nula.

El estadístico de prueba es:

Si H0 es cierta y el número de columnas y/o de filas es moderadamente grande la distribución de F se aproxima a una chi-cuadrado con k - 1 grados de libertad; de forma que se rechaza la hipótesis nula para valores de F superiores al valor crítico para el nivel de significación fijado.

PRUEBA Q DE COCHRAN

Cuando sobre n elementos se observa la serie de respuestas de cada uno de ellos a k ''tratamientos'' esta prueba permite contrastar la hipótesis nula de que no existe diferencia significativa entre los k ''tratamientos''. También es posible utilizarla si cada tratamiento se aplica a uno de los elementos de n grupos de k elementos elegidos de forma que los elementos de cada grupo se asemejen lo más posible entre ellos.

Esta prueba es adecuada cuando la respuesta a cada tratamiento es una variable dicotómica, siendo X = 1 si la respuesta es ''éxito'' y X = 0 si es ''no éxito'' Si la respuesta es susceptible de medición en por lo menos una escala ordinal también es posible dicotomizarla, pero se pierde información y, por lo tanto, es preferible utilizar la prueba de Friedman.

Los datos se disponen en una tabla de la misma forma que para la prueba de Friedman, pero ahora las columnas de la tabla contienen únicamente ceros y unos, de forma que la suma de los valores de la j-ésima columna, GJ , es el número de ''éxitos'' de la distribución de las n respuestas al j-ésimo ''tratamiento''. Si la hipótesis nula es cierta las diferencias entre el número de éxitos de cada columna se deben al azar, por lo que es de esperar que sean pequeñas, es decir, que todas las G_{j estén muy próximas al número medio de éxitos por muestra, El estadístico de prueba se basa en la dispersión del número de éxitos de cada ''tratamiento'' con respecto a :

El estadístico de prueba es:

Donde Li es el total de ''éxitos'' del primer elemento o grupo.

Si la hipótesis nula es cierta, la distribución de Q puede aproximarse mediante una chi-cuadrado con k - 1 grados de libertad y se rechaza la hipótesis nula si el valor de Q es superior al valor crítico para el nivel de significación deseado.

REALIZACIóN DE LOS CONTRASTES

Para realizar estas pruebas la secuencia es:

Analizar

Pruebas no paramétricas

k muestras relacionadas

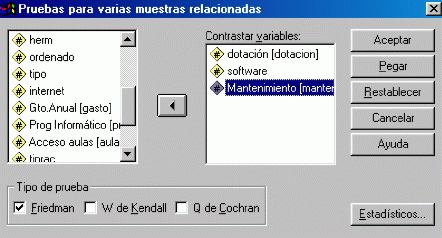
En el cuadro de diálogo Pruebas para varias muestras relacionadas se indican las variables que se quiere comparar y se activan las pruebas que se desea realizar. Por defecto está activada la prueba de Friedman.

EJEMPLO

Con los datos de la encuesta Encinf.sav probar si hay discrepancia entre la valoración que hacen los alumnos al mantenimiento (Manten), acceso a las aulas de informática (Aulas) y la valoración que hacen a los monitores que supervisan las aulas (Monitor).

Como se trata de contrastar la hipótesis nula de que las valoraciones asignadas por los alumnos a las características mantenimiento, acceso y monitores de las aulas no difiere significativamente a partir de las puntuaciones asignadas por los mismos individuos, las muestras resultantes no son independientes. Por otra parte, las variables se miden en una escala ordinal, y por tanto el contraste más adecuado es la prueba de Friedman.

Para realizar este contraste la secuencia es:

Analizar > Pruebas no paramétricas > k muestras relacionadas.

En el cuadro de diálogo se seleccionan las variables Manten, Aulas y Monitor y se mantiene el tipo de prueba activado por defecto, Friedman.

Los resultados que se obtienen son los siguientes:

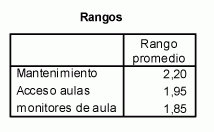
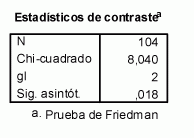
El estadístico de prueba es igual a 8,040, por lo que no se puede rechazar la hipótesis nula para niveles de significación superiores a 0,018. Al 5% de nivel de significación se acepta la hipótesis de que no existen diferencias significativas entre las valoraciones asignadas por los alumnos a estas características.