ANÁLISIS EXPLORATORIO DE DATOS

El análisis exploratorio tiene como objetivo identificar el modelo eórico más adecuado para representar la población de la cual proceden los datos muestrales. Dicho análisis se basa en gráficos y estadísticos que permiten explorar la distribución identificando características tales como: valores atípicos o outliers, saltos o discontinuidades, concentraciones de valores, forma de la distribución, etc. Por otra parte, este análisis se puede realizar sobre todos los casos conjuntamente o de forma separada por grupos. En este último caso los gráficos y estadísticos permiten identificar si los datos proceden de una o varias poblaciones, considerando la variable que determina los grupos como factor diferenciador de las poblaciones. También permite comprobar, mediante técnicas gráficas y contrastes no paramétricos, si los datos han sido extraídos de una población con distribución aproximadamente normal.

Para realizar un análisis exploratorio, la secuencia de instrucciones es:

Analizar
	Estadísticos Descriptivos
		Explorar

• Si el análisis de la variable se realiza conjuntamente para todos los casos es suficiente indicar la o las variables en la ventana Dependientes.

• Si el análisis de la variable se realiza por grupos es necesario indicar también la variable que define los grupos en la
ventana Factores.

Opcionalmente se puede indicar en la ventana Etiquetar los casos mediante una variable cuyos valores se tomarán para etiquetar los outliers.

El análisis exploratorio calcula, por defecto, los estadísticos más importantes así como el intervalo de confianza para la media al 95%, el gráfico de tallo y hojas y el diagrama de caja. Para ampliar éste análisis se puede acceder a los siguientes cuadros de diálogo intervalo media:

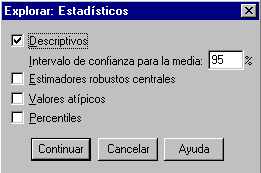
• Estadísticos: Permite modificar el grado de confianza del intervalo para la media, calcular Estimadores robustos centrales (estimador M de Huber, estimador en onda de Andrews, estimador M redescendente de Hampel, estimador biponderado de Tukey), y hallar los Valores atípicos (se obtienen los 5 mayores y los 5 menores valores de la distribución) y algunos Percentiles (los cuartiles y el 5º, 10º, 90º y 95º centil).

• Gráficos:

	- Las opciones del Diagrama de caja se utilizan sólo cuando se han seleccionado varias variables dependientes. Por defecto, se presentan en gráficos distintos las variables dependientes seleccionadas, y para cada una de ellas, en el mimo gráfico, las cajas de los distintos grupos definidos por el factor. Si se selecciona Dependientes juntas se representan en un único gráfico las cajas correspondientes a todas las variables dependientes. Con la opción Ninguno se omite la presentación de los diagramas de caja.
	- Las alternativas de Descriptivos son el gráfico de tallo y hojas, activado por defecto, y el histograma. Estos gráficos se elaboran por separado para todos los grupos definidos para cada una de las variables dependientes.
	- Si se activa la opción Gráficos con pruebas de normalidad se obtienen para cada una de las variables dependientes y para cada uno de los grupos el correspondiente gráfico Q-Q Normal y el gráfico Q-Q Normal sin tendencia. Estos gráficos permiten comprobar si las poblaciones de las que se han extraído las muestras presentan distribución normal. El Q-Q Normal presenta simultáneamente para cada elemento el valor observado y el valor esperado bajo el supuesto de normalidad. Si los datos proceden de una distribución normal los puntos aparecen agrupados en torno a la línea recta esperada. El Q-Q Normal sin tendencia se basa en las diferencias entre los valores observados y los valores esperados bajo la hipótesis de normalidad. Si estas diferencias se distribuyen aleatoriamente alrededor del eje de abscisas puede suponerse que la hipótesis de normalidad es sostenible. Además, esta opción permite contrastar la hipótesis de normalidad con las prueba de Kolgomorov-Smirnov* y de Shapiro-Wilks*.
	- La opción Dispersión por nivel con prueba de Levene, activando No transformados, permite contrastar la hipótesis de igualdad de varianza para los grupos definidos por un factor.

• Opciones controla el tratamiento de los valores missing en el análisis exploratorio.

•	- Por defecto está activada la opción Excluir casos según lista con la que se eliminan de todos los cálculos y gráficos los casos que presentan algún valor missing, ya sea en alguna de las variables dependientes o en algún factor. Con esta opción el número de casos válidos es el mismo en todos los resultados.
	- Si se activa Excluir casos según pareja, los casos que presentan algún valor missing en alguna variable dependiente sólo se excluyen en los cálculos de estadísticos correspondientes a dicha variable, y sí que se incluyen en los de otras variables dependientes. Con esta opción el número de casos válidos no tiene porque coincidir en todos los resultados.
	- Con la opción Mostrar valores, los valores missing de un factor definen un nuevo grupo de casos. Si los valores missing son de la variable dependiente éstos no se incluyen en el cálculo de los estadísticos.

El análisis exploratorio de datos puede aplicarse a variables cuantitativas. La variable factor debe presentar un número limitado de categorías y es conveniente expresarlas numéricamente o con una cadena alfanumérica corta.

EJEMPLOS

Ejemplo 1.

Con la base de datos Enctran.sav realizar el análisis exploratorio básico de las variables: Alt y Peso, diferenciando por las variables Genero y Curso. Etiquetar los valores atípicos con la variable Num.

En el cuadro de diálogo Explorar se seleccionan las siguientes variables:

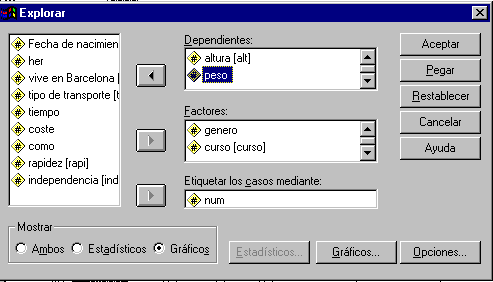
Con ello se obtendrá el análisis exploratorio básico de las variables dependientes (Altura y Peso). Los factores Género y Curso son variable cualitativas con dos modalidades cada una; por lo tanto, para cada dependiente quedarán definidos dos grupos con respecto al género (Hombres y Mujeres) y dos con respecto al curso (Primero y Segundo). La variable Num se selecciona para etiquetar los valores outliers.

Los resultados que se obtienen con las opciones activadas por defecto son:

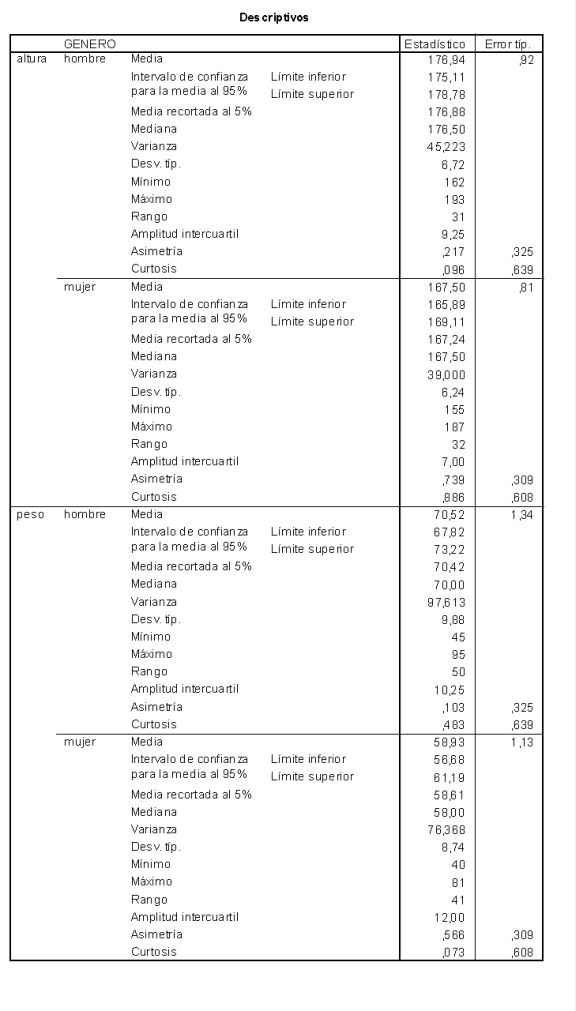
• Descriptivos:

Contiene los valores de los estadísticos más utilizados para las variables Altura y Peso en función de los grupos inducidos por las variables factores. En la tabla siguiente se recogen los resultados de ambas variables correspondientes a los grupos asociados al factor Genero. El lector puede comprobar que el output contiene también el cuadro análogo correspondiente a los grupos definidos por elfactor Curso.

• Gráficos:

En el visor de resultados se obtienen los gráficos de tallo y hoja y los diagramas de caja.

Como puede observarse la distribución de la variable Altura para el grupo mujer presenta dos outliers o valores extremos, con valores superiores a 182 cm. Gráficos similares se obtienen también para el resto de combinaciones variable-factor.

En el diagrama de caja anterior se observa que el valor central de la distribución de la variable Altura es notablemente superior en el grupo de hombres; la distribución de la altura en ambos grupos es prácticamente simétrica y, aparentemente, presentan dispersiones parecidas. Obsérvese que los valores outliers están etiquetados con el número de caso.

Ejemplo 2.

Para las mismas variables del ejemplo anterior y diferenciando únicamente por el factor género comprobar:

• La hipótesis de que las muestras provienen de poblaciones normales;
En el cuadro de diálogo que se abre con la secuencia Analizar > Explorar > Gráficos se activa la opción Gráficos con pruebas de normalidad:

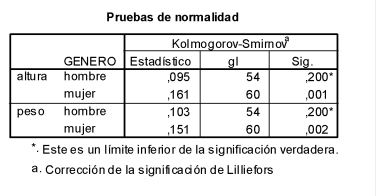
El estadístico del contraste Kolmogorov-Smirnov para la variable Altura en el grupo hombres toma el valor 0,95 que no permite rechazar la hipótesis nula de normalidad para niveles de significación inferiores a 0,2. En el grupo de mujeres, por el contrario, el estadístico toma el valor 0,161 con el que se rechaza la hipótesis de normalidad para niveles de significación superiores a 0,001. De la misma forma se interpretan los resultados correspondientes a la variable peso.

En el gráfico Q-Q normal de la variable Altura se observa, para el grupo de los hombres, que los puntos están situados casi sobre la línea recta lo cual es un indicio de normalidad de la población de origen. Este resultado es compatible con el del contraste de Kolmogorov-Smirnov.

• La hipótesis de que las muestras provienen de poblaciones con igual varianza.

Esta prueba debe realizarse cuando se desea contrastar hipótesis referidas a las medias de dos o más poblaciones definidas mediante una variable factor.

En el cuadro de diálogo Explorar: Gráficos se activa la opción No transformados del recuadro Dispersión por nivel con prueba de Levene.

El estadístico de Levene, en todos los casos, permite no rechazar la hipótesis de homogeneidad de la varianza (obsérvese que los niveles de significación para los que se rechazaría esta hipótesis son todos superiores a 0,4, por lo tanto, para los niveles de significación habituales no se rechaza la hipótesis nula).