CONTRASTES DE NORMALIDAD

Un caso específico de ajuste a una distribución teórica es la correspondiente a la distribución normal. Este contraste se realiza para comprobar si se verifica la hipótesis de normalidad necesaria para que el resultado de algunos análisis sea fiable, como por ejemplo para el ANOVA.

Para comprobar la hipótesis nula de que la muestra ha sido extraída de una población con distribución de probabilidad normal se puede realizar un estudio gráfico y/o analítico.

PRUEBA DE KOLMOGOROV-SMIRNOV

Cuando la prueba Kolmogorov-Smirnov kolmogorov se aplica para contrastar la hipótesis de normalidad de la población, el estadístico de prueba es la máxima diferencia:

siendo Fn(x) la función de distribución muestral y Fo(x) la función teórica o correspondiente a la población normal especificada en la hipótesis nula.

La distribución del estadístico de Kolmogorov-Smirnov es independiente de la distribución poblacional especificada en la hipótesis nula y los valores críticos de este estadístico están tabulados. Si la distribución postulada es la normal y se estiman sus parámetros, los valores críticos se obtienen aplicando la corrección de significación propuesta por Lilliefors.

PRUEBA DE SHAPIRO-WILK

Cuando la muestra es como máximo de tamaño 50 se puede contrastar la normalidad con la prueba de shapiro Shapiro-Wilk. Para efectuarla se calcula la media y la varianza muestral, S2, y se ordenan las observaciones de menor a mayor. A continuación se calculan las diferencias entre: el primero y el último; el segundo y el penúltimo; el tercero y el antepenúltimo, etc. y se corrigen con unos coeficientes tabulados por Shapiro y Wilk. El estadístico de prueba es:

donde D es la suma de las diferencias corregidas.

Se rechazará la hipótesis nula de normalidad si el estadístico W es menor que el valor crítico proporcionado por la tabla elaborada por los autores para el tamaño muestral y el nivel de significación dado.

La secuencia para realizar los contrastes de normalidad es:

Analiza

Estadísticos Descriptivos

Explorar

En el cuadro de diálogo que aparece al activar el botón Gráficos se activa la opción Gráficos con pruebas de normalidad.

EJEMPLO

Ejemplo 1.

Con los datos correspondientes a la variable Trans de la encuesta Enctrans.sav y con referencia a los encuestados que viven en Barcelona, se quiere comprobar si su distribución en cuanto al tipo de transporte utilizado se adapta a los resultados de un estudio realizado por el Ayuntamiento de Barcelona, que son los siguientes: el 40% de los desplazamientos al trabajo se realizan en metro; el 30% en autobús; el 20% en transporte privado y 10% otros medios.

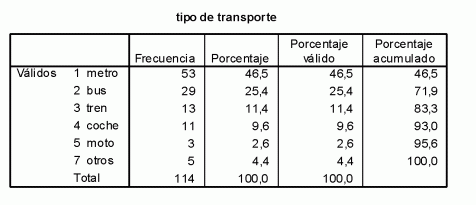
La distribución de frecuencias de la variable Trans es:

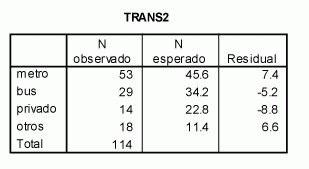
En este caso para realizar el contraste Chi-cuadrado es necesario definir las cuatro categorías contempladas en la hipótesis nula. Para ello, se crea una nueva variable, Trans2, a partir de Trans con las siguientes categorías: Metro, Bus, Privado (que resultará de agregar Coche y Moto) y Otros (que agrupará Tren y Otros).Una vez creada la nueva variable, con la secuencia Analizar > Pruebas no paramétricas > Chi-cuadrado se llega al cuadro de diálogo en donde se selecciona la variable Trans2 y se introduce en Valores esperados las frecuencias relativas de cada categoría según la hipótesis nula correctamente ordenadas: 0,4 para la categoría 1; 0,3 para la 2; 0,2 para la 3 y 0,10 para la 4. Al aceptar se obtienen los siguientes resultados:

Como todas las categorías presentan frecuencia esperada mayor que 5 se puede aplicar el contraste Chi-cuadrado sin modificar el número de categorías. El valor del estadístico Chi-cuadrado permite rechazar la hipótesis nula para niveles de significación superiores al 2,7%. Así pues, al 5% de significación se llega a la conclusión de que la distribución del tipo de transporte que utilizan los alumnos no se adapta a la publicada por el ayuntamiento.

Ejemplo 2.

Con la información correspondiente a la variable Pla de la base de datos Encinf.sav, se desea comprobar si la valoración que realizan los alumnos del plan de estudios sigue una distribución uniforme.

Para realizar la prueba de bondad de ajuste Kolmogorov-Smirnov la secuencia a seguir es Analizar > Pruebas no paramétricas> K-S de 1 muestra. Se selecciona la variable Pla de la base de datos Encinf.sav y se indica que la Distribución de contraste es uniforme.

Los resultados son:

A la vista de los resultados se concluye que no se puede rechazar la hipótesis de que la valoración asignada por este grupo de alumnos al plan de estudios es uniforme para cualquier nivel de significación inferior al 7,1%.

Ejemplo 3.

Con la base de datos Encinf.sav, se desea comprobar si la variable gasto presenta una distribución normal.

Para realizar la prueba de normalidad la secuencia a seguir es Analizar> Estadísticos Descriptivos> Explorar. Se selecciona la variable Gasto y en el cuadro de diálogo correspondiente a los Gráficos se activa la opción Gráficos con pruebas de normalidad.

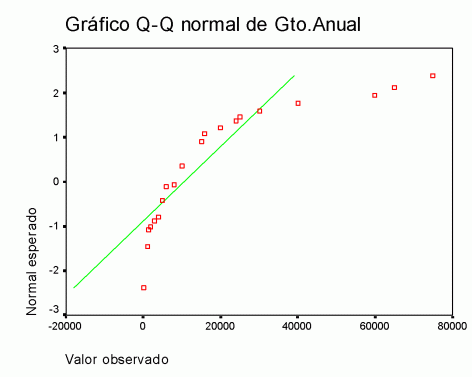
Los resultados obtenidos son:

El estadístico de prueba Kolmogorov-Smirnov con la correción de Lilliefors presenta un nivel de significación igual a 0,000. Enconsecuencia se rechaza la hipótesis de normalidad. El gráfico Q-Q normal ratifica la conclusión anterior, ya que los valores observados no se situan sobre la recta esperada bajo el supuesto de normalidad.