Scripta Nova |
CONTRIBUCIÓN AL ESTUDIO DE LAS DESIGUALDADES EN LA ESPAÑA DE LOS ’60: INGRESOS Y ALIMENTACIÓN
Pablo Martinelli Lasheras
Department of History & Civilization – European University Institute
pablo.martinelli@eui.eu
Recibido: 6 de marzo de 2008. Devuelto para revisión: 7 de mayo de 2009. Aceptado: 21 de mayo de 2009.
FINALISTA DEL PREMIO ISIDORO DE ANTILLÓN 2008 PARA TRABAJOS DE MÁSTER
Contribución al estudio de las desigualdades en la España de los '60: ingresos y alimentación (Resumen)
Las transformaciones que afectaron a la economía y a la sociedad española durante los sesenta han sido hasta ahora insuficientemente estudiadas desde la perspectiva de su impacto en los niveles de bienestar. Así, se propone aquí un método para superar los obstáculos metodológicos que hasta el momento han impedido evaluar indicadores provinciales de desigualdad en la distribución de los ingresos a partir de la Encuesta de Presupuestos Familiares de 1964-1965, y se evalúa la relación existente los mismos y diferentes variables. A continuación se estudian las estructuras provinciales de la alimentación y se realiza una estimación de sus determinantes y de sus diferencias. Finalmente se realiza una estimación de la huella ecológica provincial de la alimentación.
De este modo se muestra el grado de complejidad existente entre los ingresos, su distribución social y territorial y algunos de los elementos que definen el nivel de bienestar de una sociedad.
Palabras clave: bienestar, desigualdad, ingresos, alimentación, huella ecológica.A Contribution to the Study of Inequality in Spain during the Sixties: Income and Food Consumption (Abstract)
The transformations that affected the Spanish economy and society during the sixties have been up to now insufficiently studied from the perspective of their impact on well-being levels. Thus, here it is proposed a method to overcome the methodological obstacles that have avoided the evaluation of provincial income inequality indexes from the Spanish Household Budget Inquiry of 1964-1965 and it is studied the relationship between those indexes and some variables. Then, the study turns to the differences in provincial levels of food consumption and their determinants. An estimation of the provincial ecological footprint of diets (as an index of their sustainability) follows.
As a conclusion, the relationship between income levels, their social and territorial distribution and some of the main items which define the welfare of a society seem to be much more problematic and complex than what an excessively simplistic version of the mainstream economic theory may suggest.
Key words: well-being, inequality, income, food, ecological footprint.MARCO TEÓRICO Y FUENTES
Durante la década de los ’60 España vivió su particular “edad de oro” y uno de los periodos de transformaciones más radicales de toda su historia en su economía y su sociedad. La década que empezó con el Plan de Estabilización acabó con una país ya plenamente industrial, atravesado por el movimiento interior y exterior más grande de personas de su historia, con un campo que se fue vaciando rápidamente y, consecuentemente, se fueron imponiendo transformaciones de su agricultura que la alejaron definitivamente del modelo de la agricultura tradicional; fue esta la década de mayor crecimiento económico del siglo XX (y por extensión de la historia). Lo único que se mantenía intacto era el sistema político, que hacía del tardo-fascismo y del nacional-catolicismo español la gran anomalía del concierto europeo, junto a su vecino ibérico. De manera que en España los años gloriosos del capitalismo keynesiano, amén de empezar con notable retraso respecto al resto del mundo capitalista avanzado, se caracterizaron por una particular cojera en la aplicación del modelo occidental de la época; una cojera consolidada de la mano de los intereses militares y geopolíticos estadounidenses y acentuada por las transformaciones a que obligaba una desastrosa crisis de balanza de pagos. Es decir, se asistió a una inédita aceleración del crecimiento pero sin paralela construcción del Estado de Bienestar. ¿Cómo influyó esta circunstancia sobre los niveles de bienestar de los españoles y las españolas? ¿De qué magnitud eran durante este período las desigualdades y cómo evolucionaron? Responder a estas preguntas desde la perspectiva de los ingresos y de la alimentación es el objetivo de esta investigación.
La multidimensionalidad del bienestar
En los últimos años la solidez del marco teórico neoclásico, que parecía haber alcanzado unos niveles de hegemonía inexpugnables, se ha visto sometido a una serie de críticas que han puesto en evidencia los límites de sus supuestos teóricos y, por ende, de su capacidad como herramienta para explicar la realidad. Dichos ataques han provenido a veces de los confines mismos del paradigma neoclásico y en otros se han situado abiertamente fuera del mismo, pero sus efectos sobre la puesta en discusión de verdades que parecían ya definitivamente establecidas han sido igualmente efectivos y estimulantes.
Una de las críticas más poderosas proviene de las aportaciones de Amartya Sen. Dos conjuntos de sus numerosas observaciones pueden ser especialmente invocados a la hora de explicar las razones que justifican esta investigación: la complejidad de las categorías de bienestar, por una parte, y la complejidad de la toma de decisiones por parte de las personas, por otra.
Por una parte, Sen se ha referido a los límites de medir los niveles de bienestar únicamente por una sola variable: los ingresos monetarios. Esto se enmarca en una reflexión más general acerca de lo que consideramos como “bienestar” y de una clara sistematización de los elementos que intervienen en su formación. Hay que tener claro, por una parte, que el ser humano tiene una serie de necesidades. Algunas de éstas son de carácter universal; de hecho, varias pueden considerarse de origen genético e inseparables de lo que entendemos como naturaleza humana en sentido biológico o zoológico, a decir de antropólogos como Marvin Harris[1]; otras necesidades no están directamente vinculadas a un imperativo genético y pueden más bien considerarse fruto de la selección cultural. Otras propuestas de sistematización de las necesidades humanas han sido realizadas desde diferentes tipos de disciplinas, e incluso no existe consenso sobre qué tipo de necesidades deben considerarse de origen genético y cuáles de origen cultural[2]. Pero lo que aquí nos interesa resaltar es que todas estas propuestas comparten una característica: la pluralidad de las necesidades y los límites a la agregabilidad de las mismas. Cada necesidad es única, indivisible e insubsumible en otra. La satisfacción de las necesidades genera lo que entendemos por bienestar; dada la multiplicidad de necesidades a satisfacer y su insustituibilidad, parecen evidentes las dificultades de realizar ordenaciones de niveles de bienestar y comparaciones interpersonales e intertemporales de los mismos. Respirar es tan importante para sobrevivir como comer, porque las funciones vitales no pueden desarrollarse en estados de carencia de alguno de los dos elementos. Lo mismo puede decirse de cada uno de los elementos que podemos considerar “necesidades”: no son intercambiables entre sí. ¿Disfruta de un nivel de bienestar superior un enfermo rico o un pobre sano? En otros términos: sea W(x,y) una función de bienestar con solamente dos ítems, X e Y (dos necesiadades). Sean los individuos A y B. Sean XA,YA y XB,YB las cantidades de los diferentes ítems de bienestar disfrutados por A y B (los satisfactores de necesidades). Si XA>XB e YA<YB, lo que se plantea es que no es posible establecer irreversiblemente si WA es mayor, menor o igual a WB.
Todo esto no obsta a que puedan realizarse jerarquías entre necesidades o grupos de necesidades y, en consecuencia, establecer gradaciones en los grados de satisfacción de las mismas y por tanto en los niveles de bienestar alcanzados. Lo que cabe resaltar es que dichas gradaciones no pueden nunca reclamar un carácter absoluto e indiscutible. En el ejemplo antes citado, pues, es posible, legítimo y quizás necesario realizar supuestos sobre la forma de la función de bienestar, que viene a ser lo mismo que realizar supuestos sobre los criterios de agregación entre variables. Pero dicho ejercicio debe resaltar explícitamente los criterios adoptados y ser consciente de la subjetividad de los mismos.
El debate sobre los niveles de bienestar debe, por tanto, enmarcarse en un contexto de ciencia dialogada, en el que los diferentes participantes aporten sus propios elementos al debate con predisposición al intercambio de ideas y con plena conciencia de la parcialidad de sus aportaciones; que cada cual explicite su punto de vista, y que los más elijan (con conocimiento de todas las posiciones) las opciones o los conjuntos de opciones que consideren más cercanos a la verdad; acaso pueda esto despertar el temor a la incertidumbre, al indeterminismo y a la inoperatividad de la actividad científica. Quizás estos temores sean justificados. Pero también es cierto, por una parte, que nos emancipa de servidumbres hacia verdades tenidas por científicas a pesar de su indemostrabilidad y, por otra, que las ciencias sociales pecarían de imperdonable presuntuosidad caso de perseverar en la pretensión de establecer verdades absolutas vinculadas a la predictibilidad cuando otras ramas de las ciencias, ante la evidencia de que estamos en un mundo rodeado de incertidumbre, hace ya tiempo que las han abandonado. Pero nos estamos alejando en exceso del núcleo de nuestra argumentación.
Hemos establecido que para satisfacer cada una de sus necesidades los seres humanos pueden disponer de una serie de elementos, que Sen llama “satisfactores”. También hemos resaltado las dificultades de agregarlos entre sí. Cada vez parece más claro que centrarse únicamente en los indicadores monetarios del bienestar, tales como los niveles de ingresos, es una opción excesivamente reduccionista. Deben tenerse en cuenta otros elementos de dimensiones diferentes (esto es, no monetarias), y esto dificulta la evaluación de los niveles de bienestar. En este sentido, un buen marco analítico para evaluar las diferencias en los niveles de bienestar puede ser el análisis multicriterial, que la economía ecológica propone para evaluar entre diferentes alternativas que implican diferentes resultados para diferentes variables de problemática agregación. El método consiste, en síntesis, en utilizar diferentes ponderaciones para agregar las variables y presentar todos los resultados. En caso de que una alternativa domine en forma robusta (para todos los conjuntos de ponderaciones posibles) sobre las otras, ciertamente es la mejor. En caso contrario, la mejor alternativa dependerá de los criterios de agregación que se prefieran (es decir, qué peso se quiere dar a cada una de las variables en la evaluación del resultado final). Como no existe una opción dominante, se presentan todos los resultados y se hace explícita la multiplicidad de criterios utilizados para evaluar y los cambios en los resultados consecuencia de los cambios en los criterios considerados.
La economía del bienestar empieza a moverse en esta dirección para de evaluar el bienestar de las personas. El ejemplo más conocido es el Índice de Desarrollo Humano, elaborado anualmente por el Programa de Naciones Unidas para el Desarrollo (PNUD) y ampliamente popularizado[3]. En la misma publicación anual también suelen consignarse otros indicadores, menos conocidos por el gran público, pero de análoga filosofía: el Indicador de Pobreza Humana para países en desarrollo (IPH-1), el Indicador de Pobreza Humana para una selección de países de la OCDE (IPH-2), el Índice de Desarrollo Relativo de Género (IDG) y el Índice de Potenciación de Género[4]. Todos estos indicadores comparten una filosofía de fondo, basada en la doble multidimensionalidad de las ordenaciones del bienestar: a) el bienestar no puede ser medido atendiendo únicamente a una variable, por ser consecuencia de la interacción de más variables; b) incluso utilizando ciertos criterios de agregación, los indicadores obtenidos no pueden pretender reflejar totalmente los niveles de bienestar y deben ser comparados con otros indicadores alternativos que utilizan variables y/o criterios diferentes.
Pero incluso atendiendo a una sola dimensión del bienestar (los ingresos) cada vez se abre paso más la idea de que, en aras de realizar comparaciones entre agregados sociales, limitarnos a los valores medios es excesivamente reduccionista y puede llevar a conclusiones erróneas; hace falta atender también a su distribución dentro de los agregados a comparar. Así, siguiendo a Cowell[5], se hace necesario incluir en las funciones de bienestar social argumentos tanto referidos a los niveles de renta como a su distribución, en funciones del tipo W=ω[μ(y), I(y)][6]. Discutiremos más adelante algunas formas concretas de funciones de bienestar que cumplen estos requisitos. Lo que aquí interesa es que incluso centrándonos en una sola categoría definitoria del bienestar, se hace necesario aproximarse a diferentes dimensiones de la misma (aquí, sus niveles medios y su distribución).
Evidentemente, si damos por buena, por una parte, la necesidad de atender tanto a los niveles como a su distribución dentro de la unidad de análisis de un ítem de bienestar para realizar comparaciones de bienestar más completas y si, por otra, admitimos la multidimensionalidad de los ítems de bienestar, las desigualdades de bienestar también deberán evaluarse de acuerdo con criterios multidimensionales; habrá que ver en qué ítems de bienestar existe una mayor desigualdad y en cuáles no: si en el acceso a diferentes satisfactores de diferentes necesidades existen desigualdades (tanto entre unidades de análisis como dentro de las mismas) similares, entonces quiere decir que existe una correspondencia lineal o, cuanto menos, funcional entre los mismos. Si este fuere el caso, podrían reducirse a una única unidad de medida los indicadores de bienestar, sin riesgo de perder de vista demasiada información y con la ventaja de simplificar notablemente el análisis. Sin embargo no con todos los ítems de bienestar pueden considerarse tales supuestos válidos, como estamos argumentando.
¿Igualdad de qué?, se pregunta Amartya Sen[7]; si el bienestar tiene diferentes dimensiones, también la desigualdad debe reflejar ese carácter multidimensional, por lo menos para cierto número de ítems de bienestar. No solo cuenta la desigualdad en los ingresos, también, por ejemplo, puede contar la desigualdad en la esperanza de vida, la desigualdad en los niveles de nutrición, la desigualdad en los niveles de precariedad laboral, la desigualdad en la capacidad de incidir políticamente en el proceso de toma de decisiones que afectan a la colectividad, etc.
De este modo el panorama sobre los niveles de bienestar aparece como sustancialmente más complejo de lo que había sido considerado hace años: ya no nos basta reducirnos a los ingresos monetarios. El bienestar de una sociedad es multidimensional y queda definido por diferentes variables. La desigualdad forma parte de lo que define el bienestar de una sociedad y, a la vez, debe considerarse en todas las dimensiones relevantes del bienestar.
La presente investigación pretende contribuir al esfuerzo colectivo por esclarecer la historia del bienestar y las desigualdades en España. La atención se focalizará en dos aspectos concretos del bienestar, los ingresos y la alimentación, sus respectivas desigualdades y la relación entre ambas. El periodo de análisis son los años `60 del siglo XX. Es evidente que con esto solamente llegaremos a hacer un poco de luz sobre los niveles de bienestar: por una parte porque limitamos considerablemente en el tiempo nuestro análisis y, por otra (y quizás más importante), porque nos centraremos solamente en dos ítems de bienestar. Somos conscientes de los límites que esto supone, pero los afrontamos desde la profunda convicción de que la complejidad del tema de los niveles de bienestar hace preferible una aproximación parcial y plenamente consciente de ello que una aproximación que pretenda reducir los análisis de las desigualdades y del bienestar a unas pocas variables. Si consideramos que la relación entre los distintos elementos que definen el bienestar es compleja, y por tanto no pueden reducirse todos a una misma unidad de medida, ¿porqué no analizarlos uno a uno y evaluar los resultados, en vez de intentar definir agregaciones, necesariamente cargadas de juicios de valor, que pretendan a priori seleccionar los ítems de bienestar relevantes e imponer un criterio de agregación entre ellos? ¿Porqué no analizar los niveles y su distribución de los diferentes ítems de bienestar de manera individual y dejar al juicio de cada investigador u observador interesado la tarea de seleccionar entre los más y los menos relevantes?
Como las variables que intervienen son numerosas, estudiarlas una a una del modo más profundo posible no puede ser más que una tarea colectiva, como ya se ha señalado.
Aquí, pues, evaluaremos por una parte las desigualdades en los niveles de ingresos, tomando las provincias como unidades de análisis. Construiremos diferentes indicadores de las desigualdades en los ingresos dentro de cada provincia, tarea hasta ahora inédita para los años en cuestión, y los compararemos entre ellos. Veremos así qué provincias eran las que presentaban mayores niveles de desigualdad y veremos si esta presenta algún patrón reconocible de relación con la renta: ¿Puede establecerse una relación entre nivel de ingresos y desigualdad, aunque sea de ida y vuelta como predice la “curva de Kuznets”?
En segundo lugar estudiaremos las diferencias provinciales en la alimentación, exploraremos cuáles son sus determinantes y veremos si existe una relación directa entre ingresos monetarios y niveles de alimentación, y por extensión entre desigualdades monetarias y desigualdades alimentarias.
Finalmente, estimaremos la huella ecológica de la alimentación para cada provincia (un indicador del impacto ambiental de las desigualdades en las dietas, y por tanto de su grado de sostenibilidad en el tiempo), estudiaremos su distribución territorial y veremos si, también en este caso, los ingresos presentan alguna relación, y de qué tipo, con el espacio ocupado por la alimentación efectiva de los habitantes de las diferentes provincias.
Fuentes: la Encuesta de Presupuestos Familiares de 1964-1965
Un buen aliciente para afrontar este periodo, al margen de las cuestiones que de por sí despierta, es que contamos con información disponible no suficientemente explotada. Arrojar algo más de luz sobre este periodo es pues, además de necesario, posible. La piedra de toque de nuestra aproximación será la primera gran Encuesta de Presupuestos Familiares realizada en España, la de 1964; con un nivel de representatividad estadística y de desagregación (territorial y temática) de los datos con los que no cuenta la EPF de 1958 (la primera realizada en absoluto en el Estado), esta encuesta es la primera cuyos datos pueden ser explotados satisfactoriamente a nuestros efectos. Su elaboración presenta mejoras notables respecto a la EPF-1958. Se realizó durante un año, de marzo de 1964 a marzo de 1965 (para captar la estacionalidad en el consumo), se incluyeron en la muestra todo tipo de hogares (sin restricciones en función del tamaño y del nivel de ingresos), se registró un número mayor de características de la población (aunque no siempre se publicaron posteriormente con un nivel de desagregación aceptable) y, finalmente, el tamaño de la muestra asume finalmente dimensiones que la hacen realmente fiable: 20.794 hogares, de los que se consideran colaboraciones útiles 20.062 (con lo que se obtiene un porcentaje de respuestas útiles un 3-4% superior a las de la EPF-1958, legando al 96,5%), que implican a algo más de 80.000 personas. La muestra supone, pues, un 0,25% de la población. Se distingue también entre las muestras obtenidas en unidades censales urbanas y suburbanas, lo que es particularmente interesante en el caso de querer estudiar fenómenos cuyas pautas difieren en función de dichos ámbitos, como por ejemplo la distribución de los ingresos o las estructuras de consumo, como es nuestro caso.
Los resultados de la EPF fueron publicados en dos tiempos. En primer lugar, en 1965 apareció un volumen con la primera tanda de resultados, que llevaba por título “Encuesta de Presupuestos Familiares (Marzo 1964-Marzo1965). Resultados provisionales, nacionales y provinciales”. El mismo se dividía, tras una introducción metodológica sobre el proceso de elaboración de la encuesta y la posterior explotación de los datos, en dos bloques: por una parte los resultados nacionales, y por otra los resultados provinciales. Los resultados nacionales constan de series de tres tablas (conjunto nacional, conjunto urbano y conjunto suburbano[8]) de doble entrada en las que se clasifican los hogares encuestados en función del nivel de ingresos del hogar y el tipo de actividad (“categoría socio-económica”) [9] del sustentador principal. La segunda parte (los resultados provinciales) recalca en lo esencial la primera, excepto por la ausencia de algunas elaboraciones porcentuales fácilmente obtenibles a partir de los datos presentados en forma absoluta y de comparaciones con los datos de 1958 (recordemos que la ausencia de datos desagregados a nivel provincial es uno de los mayores límites de dicha encuesta). Así, tenemos, para cada provincia (siempre con datos para los dos conjuntos correspondiente a la estratificación censal y al total), la ficha técnica introductoria con datos de la población y la muestra, la distribución de los hogares por categoría y niveles de ingresos y el presupuesto por hogar (o estructura de los gastos de consumo).
Algunos años más tarde (en 1969) se publicó el resto de información con la que disponemos respecto a la EPF64-65, bajo el título “Encuesta de Presupuestos Familiares (Marzo 1964-Marzo 1965)”. Esta publicación es de inestimable valor tanto por la información que contiene como por el modo en que permite interpretar los datos aparecidos cuatro años antes. En suma, los datos publicados se refieren a: a) datos cruzados a nivel nacional de las características de los hogares (tamaño del hogar y nivel de ingresos, tamaño del hogar y categoría socio-económica); b) datos de consumo y autoconsumo de 126 categorías de alimentos (medidas en cantidades) a nivel nacional, con detalle de los conjuntos urbano y suburbano; c) datos sobre la suma de consumo más autoconsumo para los 126 tipos de alimentos a nivel regional (clasificando las provincias en 12 “regiones”), detallando eso sí los resultados para los conjuntos urbanos, suburbanos y totales; d) cantidades medias consumidas de 22 alimentos o grupos de alimentos detallados por provincias; e) datos a nivel nacional sobre el consumo de las mismas 22 categorías de alimentos recién comentadas (detallando el consumo y el autoconsumo) en función de la categoría socio-económica, en función del tamaño del hogar y en función del nivel de ingresos.
Puede verse ya ahora de la información de que disponemos que la heterogeneidad de la presentación de los datos según las variables cruzadas que de caso en caso se hayan presentado y el nivel de agregación elegido dificulta el trabajo: en algunos casos obliga a realizar estimaciones de modo indirecto mediante el paso de una variable a otra, cuando la disponibilidad de los datos cruzados lo permite, en otras obliga a realizar estimaciones mediante la realización de supuestos que parezcan razonables, y en otros casos el tipo de supuestos a realizar es tan atrevido que es imposible estimar determinadas categorías.
En 1967 y en 1968 se realizaron sendas nuevas Encuestas de Presupuestos familiares cuyos resultados se publicaron conjuntamente en 1970, aunque ambas adolecen de los mismos límites de la primera encuesta de 1958.
A partir de estas encuestas el INE realizó una Encuesta de Presupuestos Familiares con periodicidad decenal y con características similares a las de la de 1964-1965, tanto en lo relativo a la cobertura muestral (siempre sobre los como a la exhaustividad y desagregación de los datos publicados. Se realizaron en 1973-1974, 1980-1981 y 1990-1991[10]. De hecho, estas encuestas cuentan con una notable ventaja respecto a la de 1964-1965: se dispone con los microdatos informatizados. En 1965 el INE no disponía de la tecnología ni de los recursos necesarios para informatizar la información contenida en la encuesta, y esta es la razón por la que los investigadores han concentrado su atención en las encuestas posteriores[11]. Únicamente Ángel y Julio Alcaide trabajaron con los datos de la EPF64-65, aunque concentrándose en los niveles nacionales y en las diferencias en desigualdades entre categorías socio-económicas. Después pasaron a realizar estimaciones a partir de las encuestas de 1967-68, proyecciones sobre 1970 a partir de los datos de éstas últimas (siempre a nivel estatal) y empezaron luego a explotar con mayor intensidad la de 1973-74.
A partir de mediados de los años ’70 comenzó la transición política en España y la crisis económica, a continuación comenzó el proceso de descentralización competencial y política del Estado y empezó a desarrollarse, cabe notar que con varias décadas de retraso respecto a la norma europea, el Estado de Bienestar español. Como consecuencia de esto el interés de la literatura sobre la desigualdad fue centrándose en las evoluciones contemporáneas y en evaluar su interrelación con los fenómenos señalados; aunque precisamente por dichas interrelaciones la atención se ha focalizado en estudiar las desigualdades entre los diferentes territorios (por ejemplo en la convergencia en niveles de renta, en stock de capital, en niveles educativos, etc.), y la desigualdad a nivel intraterritorial sólo en años recientes ha empezado a recibir cierta atención. En todo caso, los años sesenta se han visto relegados en este tipo de análisis por esta doble razón: mayor dificultad en la manipulación de los datos y ausencia de interrelación con los procesos sociopolíticos y económicos que han confirmado el marco institucional, por una parte, y la transformación de la estructura económica, por otra, en los últimos treinta años.
En todo caso, aquí solamente se pretende exponer el abanico de datos de que disponemos para dar una idea de la densidad de información (si la comparamos con la que proporciona la EPF58, o incluso las de 1967 y 1968) o de los déficits de la misma (si la comparamos con las siguientes EPF de 1973-1974 en adelante); debe advertirse al lector de que en los sucesivos capítulos expondremos con más detalle las características de la encuesta en los aspectos relevantes que afectan al análisis de cada apartado, en tributo al rigor y la precisión, aún a riesgo de afectar a la agilidad de la lectura de algunos pasajes. Nos enfrentaremos a los inconvenientes concretos a medida que avancemos en el análisis y a medida que sea necesario realizar estimaciones y supuestos, y el lector mismo podrá juzgar en cada caso el grado de verosimilitud de unas y de exceso de audacia de otros.
LOS INGRESOS
Problemas y decisiones metodológicas
Empecemos realizando un análisis de los ingresos, uno de los principales capacitadores o mecanismos de acceso a los elementos de bienestar en las economías capitalistas. La Encuesta de Presupuestos Familiares de 1964-1965, como se ha señalado, es una fuente que contiene gran cantidad de información que ha sido escasamente explotada. Acaso, este último elemento pueda achacarse a la forma de presentación de los datos: solamente contamos con los datos publicados en papel por el INE. Desgraciadamente, no contamos con las observaciones individuales, de modo que la información está agregada a diferentes niveles (de homogeneidad diferente en función de la característica buscada). Esta situación dificulta en gran medida las posibilidades de explotar la información, especialmente cuando nos interesa comparar la correlación entre variables cuyo nivel de desagregación es diferente. Sin embargo, creemos que, a pesar de sus deficiencias, la información de que disponemos permite llegar a proyecciones razonablemente precisas, mediante una serie de estimaciones.
Entrando ya en el mérito de los obstáculos técnicos con que nos encontramos en la evaluación de las desigualdades en los ingresos y de las opciones metodológicas que tomaremos para superarlos, podemos decir que tenemos que afrontar tres tipos de dificultades: sintéticamente, las definiremos como de estratificación/ponderación, agregación y escalas de equivalencia. Afrontaremos sucesivamente estos tres tipos de problemas, aportando las decisiones metodológicas tomadas, para evaluar en una fase sucesiva los resultados obtenidos. Afrontar este tipo de problemas, explicitándolos a medida que intentemos sortearlos, y evaluar el grado de éxito que su superación pueda proporcionar viene a ser tanto como evaluar la frontera hasta la que puede llevarse la investigación de acuerdo con los datos de la EPF64-65 publicados.
El problema de las ponderacionesCabe comentar aquí algunas deficiencias que aparecen en el diseño de la muestra, que a veces (como más adelante señalaremos) pueden llevar a conclusiones distorsionadas si no son tenidas en cuenta. Esencialmente, este tipo de problemas son de dos tipos; por un lado, la representatividad provincial de la muestra: el tamaño de la muestra es similar para cada provincia (416 familias encuestadas), con lo que en las provincias con menor población la muestra es mucho más representativa que en aquellas más habitadas; en todo caso, solamente Madrid y Barcelona cuentan con muestras cuyo tamaño es menor al 0,1% de la población (0,05% en ambos casos). A parte del hecho de tener en cuenta estos elementos a la hora de evaluar las diferentes estimaciones provinciales para ser conscientes de cuales son los resultados más fiables, esta situación es relevante en otro sentido. Cuando evaluamos la media de alguna variable a nivel estatal (por ejemplo el ingreso medio o el consumo medio de algún producto) a partir de datos medios provinciales, parece obvio ponderar los datos provinciales por el peso de cada provincia en el total. A las provincias con más hogares debe asignársele mayor peso en la estructura total de la distribución de ingresos que a aquellas con menos, operación no realizada por quién ha trabajado hasta el momento con datos de la Encuesta en cuestión[12]. Si ponderamos los datos puntuales, cabe hacer lo propio con las estructuras.
El segundo elemento a tener en cuenta es similar al recién considerado, pero lejos de afectar solamente al dato estatal afecta a los propios datos provinciales. Se ha comentado que, de acuerdo con la estratificación censal, se realizaron encuestas tanto en estratos urbanos como en estratos suburbanos[13]; sin embargo, la representación de ambos estratos en las muestras provinciales no corresponden con las proporciones de los mismos en la población provincial: el porcentaje de hogares “urbanos” y “suburbanos” respectivamente encuestados en cada provincia no corresponden a las proporciones reales de la población. Los mismos elaboradores de la encuesta eran conscientes de esta circunstancia y de las distorsiones a que pudiera dar lugar; se justifica la opción tomada para garantizar que los estratos de reducido tamaño estén bien representados; de hecho existe cierta correlación inversa entre la sobrerrepresentación muestral de hogares de estratos suburbanos en cada provincia y el peso de los hogares de estratos urbanos de la población (contra más urbana era la provincia, más se representaba proporcionalmente en la muestra el área suburbana), aunque tampoco cabría descartar el peso de la otra explicación ocasionalmente ofrecida[14] (“que los trabajos de campo tengan una organización más sencilla”: es decir, organizar la ruta que minimice los desplazamientos y el coste de la encuesta).
La renuncia a la proporcionalidad en la afijación de la muestra sería indiferente si no fuera razonable suponer que existen diferencias tanto en niveles como en estructuras de las variables a investigar (aquí, ingresos, consumo y estructura de consumo) entre unos estratos y otros. Sin embargo, este no parece ser el caso: el mundo rural presenta diferencias relevantes en la estructura económica respecto al mundo urbano; estas diferencias ocupacionales y de estructura productiva se trasladan a diferencias relevantes en los niveles de ingresos y en su distribución personal, y también (como pondremos en evidencia más adelante) en las estructuras del consumo tanto en lo que se refiere a la composición de las cestas de consumo como, aún más importante, al origen del consumo mismo: en el caso del consumo de alimentos, el autoconsumo es prácticamente irrelevante en los estratos urbanos, mientras en los no urbanos supone la principal fuente de aprovisionamiento en numerosas categorías de alimentos (18 de 126) y una fuente muy relevante en la mayoría. Tampoco sería un problema la fallida proporcionalidad de la afijación de la muestra si los datos obtenidos hubieran sido corregidos en consecuencia, como hacen otros estudios sobre la distribución de la renta en España referidos a las EPF posteriores[15]; pero al menos para las estructuras de los ingresos esto no ha sido realizado ni por los editores de la encuesta ni por quien ha trabajado con los mismos (J. B. Bena Trapero y, poco después, Ángel y Julio Alcaide).
De modo que se nos vuelve a plantear aquí el problema de proyectar los datos obtenidos en los estratos urbanos y suburbanos según el peso poblacional de los mismos (y no el peso de las observaciones muestrales) para obtener información provincial más cercana a la realidad. Para ello utilizaremos los datos del censo de 1970 que (a diferencia del de 1960 y del padrón de 1965) ofrece información sobre el número de hogares en los estratos urbano, intermedio y rural (siendo la suma de estos dos últimos la correspondiente a nuestro estrato suburbano) además de los datos de población; ya que lo que estamos observando son hogares, qué mejor que utilizar su distribución como criterio de ponderación (evitando así problemas relacionados con las diferencias en los tamaños de los hogares que pueden viciar las ponderaciones en base a la población). De este modo, la distribución de los hogares entre los diferentes intervalos de ingresos para cada provincia será fruto de ponderar las distribuciones urbana y suburbana de la provincia en cuestión por la proporción de los hogares urbanos y suburbanos dentro del total de hogares de la misma; la distribución para el total español se obtendrá del mismo modo.
El problema de los datos agrupados
El siguiente problema al que debamos enfrentarnos es el hecho de contar con datos agrupados en intervalos de ingresos. Es decir, para cada provincia (y para cada Comunidad Autónoma y el total español siguiendo los criterios de ponderación señalados) disponemos de las frecuencias relativas de los hogares para 16 intervalos de ingresos. Esto es tanto como saber que, dada cada distribución provincial de los ingresos, la probabilidad de hallar un hogar con unos ingresos comprendidos entre ai y ai+1 (las marcas de clase del i-ésimo intervalo de ingresos) es fi, es decir el porcentaje de hogares sobre el total que están comprendidos en esta categoría. Para la mayor parte de medidas de la desigualdad, sin embargo, es útil asociar frecuencias a ingresos y no a intervalos de ingresos. Con la información de que disponemos podemos conocer la frecuencia relativa de los hogares entre ai y ai+1 pero no entre ai y aj (donde i<j<i+1). Podemos saber que un 9,685% de los hogares de la provincia de Almería percibe unos ingresos anuales de entre 0 y 21.600 pesetas pero ¿Cómo saber qué porcentaje del ingreso total supone esto?
La mayor parte de métodos para estimar índices de desigualdad a partir de datos agrupados solamente pueden aplicarse en caso de disponer de más información de la que nosotros disponemos. Si dispusiéramos de los ingresos medios de cada intervalo, podrían implementarse los métodos de estimar valores extremos de los diferentes índices de desigualdad entre el supuesto de máxima igualdad dentro de cada intervalo (todo el mundo percibe unos ingresos idénticos e iguales a los valores medios del intervalo) y máxima desigualdad dentro del intervalo (condicionada a que el ingreso medio continúe siendo el observado)[16], y alcanzar un compromiso entre los diferentes índices extremos (que generalmente no suelen diferir en exceso) mediante diferentes criterios de ponderación; sin embargo este no es nuestro caso, de modo que primero deberemos realizar supuestos sobre la distribución de los ingresos dentro de cada intervalo.
También puede procederse suponiendo una desigualdad nula intra-intervalos y unos ingresos medios iguales a la marca de clase de cada intervalo; es decir, el porcentaje de hogares incluido en cada intervalo recibe unos ingresos iguales a la media de los ingresos extremos que delimitan el intervalo. En ausencia de más información, este parece ser el mejor método (si no el mejor) para estimar medidas de desigualdad, como pone en evidencia un estudio realizado a partir de encuestas de presupuestos familiares en Sudáfrica (donde los datos se pueden recoger tanto con niveles exactos de ingresos como en intervalos, para desincentivar la ocultación de ingresos)[17].
Bajo estos supuestos, se halla un ingreso para cada intervalo igual a la media de los límites superior e inferior de cada intervalo. El resultado es el siguiente:
| Intervalos | Ingreso medio | |
| Límite inferior | Límite superior | |
| 0 |
21.600 |
10.800 |
21.600 |
24.000 |
22.800 |
24.000 |
30.000 |
27.000 |
30.000 |
36.000 |
33.000 |
36.000 |
42.000 |
39.000 |
42.000 |
48.000 |
45.000 |
48.000 |
54.000 |
51.000 |
54.000 |
60.000 |
57.000 |
60.000 |
72.000 |
66.000 |
72.000 |
96.000 |
84.000 |
96.000 |
120.000 |
108.000 |
120.000 |
144.000 |
132.000 |
144.000 |
180.000 |
162.000 |
180.000 |
240.000 |
210.000 |
240.000 |
500.000 |
370.000 |
500.000 |
o más |
750.000 |
De hecho, la mayor parte de los pocos estudios sobre los ingresos realizados a partir de esta encuesta han sido hechos a partir de los puntos medios de los intervalos; la estimación de la función de distribución log-normal de Bena Trapero (criticada por Alcaide) ha sido realizada tomando los puntos medios de los intervalos para hallar el porcentaje de los ingresos totales de que dispone cada frecuencia relativa de hogares. Sin embargo, ante los datos con que contamos, la implementación de este método presenta serios riesgos adicionales: el primer intervalo presenta un rango significativamente superior al de los inmediatamente siguientes y no es razonable pensar que en su interior la distribución de hogares sea uniforme; para los intervalos superiores sucede otro tanto, con el problema añadido de que el último intervalo es abierto, con lo que fijar un punto medio supone fijar arbitrariamente el límite superior.
Todo esto supone un problema porque estimamos una función de densidad a partir de haber constreñido ya los datos; de manera que primero realizamos supuestos sobre los datos y después estimamos una función que se ajusta a estos datos “modificados”. Estimar es útil para rellenar las lagunas de información de que adolecen los datos; rellenar las lagunas realizando supuestos sobre la distribución intra-intervalos y después estimar las funciones que más se ajustan a los datos manipulados de tal guisa no añade mucha información, porque la función resultante, en el mejor de los casos, se ajustará a los supuestos previamente realizados. Para esto, tanto vale trabajar con los datos directamente modificados a la hora de evaluar la desigualdad.
Otro discurso merece la distribución de Pareto. Como es sabido, la distribución de Pareto tiene una función de densidad del tipo
donde f(y) es la frecuencia relativa, y los ingresos y k y α son constantes, y particularmente esta última es conocida como “alfa de Pareto” y se interpreta como una especie de “filtro”: contra más grande es, más se “filtra” el paso de un nivel de renta a otro, de manera que menos gente se encuentra en los niveles siguientes de renta. Integrando dicha función puede verse que su función de densidad (o de distribución) acumulativa es
y su respectiva función complementaria es
donde P indica el porcentaje de población que se sitúa por encima de un determinado nivel de ingresos y. Esta última expresión puede modificarse tomando a ambos lados logaritmos y estimar los parámetros α y k por Mínimos Cuadrados Ordinarios. Sin embargo, parece haber prácticamente unanimidad sobre el hecho de que la distribución de Pareto se ajusta bien a los datos de distribución de la renta solamente para tramos de ingresos elevados, y en consecuencia suele utilizarse generalmente para estimar el nivel de ingresos del último tramo (abierto) de ingresos.
El hecho es que el uso de la distribución de Pareto no implica realizar ningún supuesto sobre la distribución intraintervalos, porque se estima a partir de la función de densidad acumulativa y aquí los valores están bien definidos: densidades acumuladas y límites de intervalo. Este método es utilizado por Alcaide en su ejercicio de estimar las distribuciones de la renta a partir de los datos de la EPF modificados combinándolos con datos de contabilidad nacional (aunque sin cuantificar tal modificación y realizando el ejercicio solamente para el total español) para las diferentes categorías socio-económicas en que queda clasificada la población (y utilizando también el método del punto medio del intervalo para la mayoría de categorías en que los resultados de tal uso parecen compatibles con los datos de contabilidad nacional) y complementándolo con una estimación del α de Pareto para calcular los ingresos medios del último tramo.
Sin embargo permanece el problema de estimar los ingresos medios del primer tramo de ingresos, cuyo rango es relativamente elevado y cuyo punto medio del intervalo subestima el ingreso medio de los hogares (puesto que, según todos los estudios realizados con microdatos, la pendiente de la función de densidad es relativamente elevada y crece rápidamente en este primer tramo: se pasa rápidamente de ingresos nulos a ingresos bajos-muy bajos). ¿Cómo resolver este problema, si es que existe forma?
Durante el estudio del problema hemos hallado una regularidad que aprovecharemos para realizar otra estimación de la distribución de los ingresos. La ventaja de este método es que también permite realizar estimaciones simplemente con los datos de las funciones de densidad acumulativas, que son las que se ofrecen cuando se dan datos agrupados, y no se necesita la media de ingresos del intervalo. Los resultados ofrecen, en todo caso, ingresos medios de cada intervalo similares al punto medio en todos los tramos excepto en el primero y en los últimos, corregidos ambos en la dirección deseada (el primero al alza, los segundos a la baja en el caso de los intervalos cerrados y con un ingreso medio del último intervalo abierto similar al ofrecido por el alfa de Pareto). El método consiste en estimar una función logística para la función de distribución acumulativa del logaritmo de los ingresos y derivar una pseudo-función de distribución de frecuencias relativas a partir de la misma. Vayamos por partes.
Nosotros disponemos de los datos agrupados de tal modo que, sin necesidad de realizar ningún supuesto sobre la distribución entre intervalos de los ingresos, podemos construir el siguiente gráfico:
 |
| Figura 1. Frecuencias acumuladas de la distribución de los hogares por intervalos de ingresos. Total España. |
Podemos así saber qué porcentaje de hogares recibe unos ingresos anuales inferiores al límite superior de cada intervalo.
El primer paso es obtener los logaritmos del límite superior de cada intervalo en que tengamos agrupados los datos. A estos podemos asociar las frecuencias acumuladas que obtengamos por suma de todos los intervalos de ingreso que quedan por debajo de cada límite superior y obtener un gráfico en todo idéntico al anterior excepto en que los límites superiores de los intervalos de ingresos están expresados en sus respectivos logaritmos. Con estos datos (frecuencias acumuladas y logaritmos de los límites superiores), podemos regresar una función logística de forma[18]
mediante estimación curvilínea. Presentamos a continuación los datos para el conjunto de España de tal regresión:
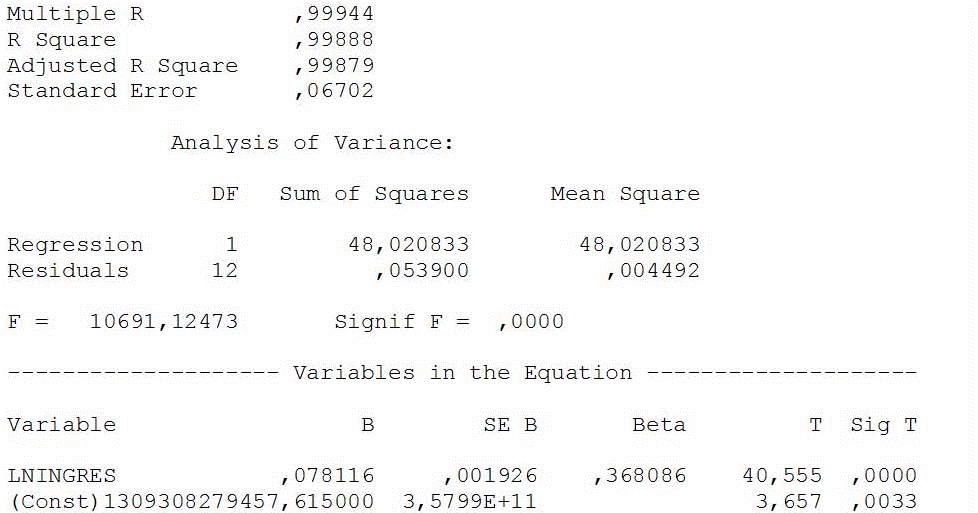
Podrá verse la muy elevada bondad del ajuste de la ecuación estimada. Presentamos también la representación gráfica de la regresión, en que los puntos representan los datos de que disponemos (las frecuencias acumuladas a cada logaritmo de los límites superiores de los intervalos) y la curva logística es la ecuación estimada. Toda función de distribución acumulativa F(x) es la integral entre 0 (o -∞, según el tipo de función) e ∞ de la función de densidad f(x)[19] de la variable en cuestión. Simétricamente, toda función de distribución de densidad es la derivada de la función de distribución. A su vez, la esperanza es la integral desde 0 (o desde -∞) de x·f(x). Desgraciadamente esta última integral, para nuestra función logística presenta el problema de incluir una función hipergeométrica de tipo 2F1, cuyas características y propiedades, hasta el presente momento, se nos escapan. Esta integral es fundamental para los estudios sobre desigualdad no sólo para calcular la esperanza, sino porque permite asociar un determinado espacio de x (léase un intervalo de ingresos) a la cuota sobre el total de los ingresos que un determinado porcentaje de población posee o al ingreso medio de un intervalo sabiendo que la población en él incluida se distribuye según la función en cuestión. Esta dificultad puede sortearse mediante la construcción de pseudo-funciones de densidad a partir de la función de distribución, realizando una aproximación discreta a la variable continua. Aprovechando el hecho de que
si construimos intervalos razonablemente pequeños entre sucesivos a y b, hallaremos las diferentes y sucesivas áreas que quedan por debajo de la función f(x) entre los diferentes a y b. Si multiplicamos el valor medio de a y b a estas áreas y las sumamos todas, tendremos una aproximación a la esperanza de la variable (o al valor medio de los ingresos, en nuestro caso) siempre que los intervalos sean razonablemente reducidos. Al fin y al cabo, integrar no es más que realizar esta operación para intervalos infinitesimalmente reducidos. Evidentemente, la bondad de la operación depende de que elijamos intervalos lo suficientemente reducidos como para que x·f(x) no se aleje demasiado de su valor teórico y lo suficientemente grandes como para que se pueda operar con ellos. Proponemos utilizar intervalos de 100 pesetas en el espacio que va de 100 a 3.000.000 (donde artificialmente fijaremos el tope de la función, puesto que los valores de F(3.000.000) son ya superiores a 0,9999 y ni los índices de desigualdad ni los ingresos medios varían perceptiblemente ampliando el espacio a valores superiores, además de ofrecer resultados extremadamente similares al uso del α de Pareto para niveles elevados de renta).
 |
| Figura 2. Frecuencias acumuladas mediante regresión logística. España. |
Ahora disponemos de todo el instrumental necesario para evaluar las desigualdades de los hogares españoles en 1965. Sin embargo, aún queda un obstáculo por salvar. Las desigualdades entre hogares no siempre reflejan totalmente las desigualdades entre personas. Sin embargo, los datos de la EPF64-65 se refieren a hogares. ¿Cómo realizar el paso de los primeros a las segundas? A este tema dedicamos el apartado siguiente.
El problema de las escalas de equivalencia
Finalmente, afrontamos nuestro último problema. La encuesta de presupuestos familiares recoge datos tomando como unidad de análisis los hogares. Sin embargo esta misma unidad no debe necesariamente ser la única que nos interesa a la hora de realizar evaluaciones de bienestar y de desigualdades, puesto que podemos querer evaluar no tanto las desigualdades entre hogares como las desigualdades entre personas. Por una parte un hogar unipersonal y uno con numerosos miembros no cuenta con las mismas necesidades (comoquiera que se decida evaluar dicha diferencia, tema que trataremos a continuación). Por otra no es necesariamente cierto que los ingresos del hogar y el tamaño de los hogares no estén de algún modo relacionados, máxime en este período en que persiste todavía en determinadas áreas del país una forma de familia ampliada en que conviven diferentes generaciones y en otras los emigrantes se asocian en las ciudades de destino en una misma vivienda, por lo menos durante un periodo inicial (tal como sucede ahora con los denominados “pisos-patera”). Desgraciadamente el hecho de no contar con los micro-datos de la encuesta nos impide asociar cada una de las familias a un determinado nivel de ingresos para poder controlar por el tamaño de los hogares. Por esta razón los índices de desigualdad calculados para estos años por los procedimientos antes descritos por Alcaide se refieren a las desigualdades entre hogares y no entre personas, con todas las salvedades que ello pueda comportar. Sin embargo, no cabe desfallecer. Creemos que es posible realizar una proyección que nos permita sortear este problema. Por una parte, contamos con las distribuciones de ingresos de los hogares agrupadas en diferentes intervalos. Por otra, contamos con la distribución de los hogares en relación a su tamaño a nivel provincial gracias al censo de 1970, el primero en recoger este tipo de información. Finalmente, contamos con un cuadro elaborado a partir de los datos de la EPF64-65 en la publicación de 1969 del mismo nombre[20] que ofrece información adicional a la publicada en 1965 (la más extensa, publicada con el subtítulo de “resultados provisionales”). En dicho cuadro se muestran los hogares (a partir de los cuales se pueden presentar los respectivos porcentajes sobre el total, sobre cada tamaño de hogar o sobre cada intervalo de ingreso) agrupados en un cuadro de doble entrada en que aparecen, precisamente, los datos cruzados que a nosotros nos interesan. A continuación se presenta el cuadro de porcentajes sobre el total obtenido a partir de dicha información.
|
Tamaño de los hogares (Porcentajes) |
|||||||||
Intervalos de ingresos (miles de pesetas) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 o más |
0 a 21,6 |
3,97 |
2,59 |
0,86 |
0,46 |
0,21 |
0,10 |
0,06 |
0,05 |
0,03 |
0,00 |
21,6 a 24 |
0,54 |
0,62 |
0,41 |
0,18 |
0,09 |
0,02 |
0,01 |
0,02 |
0,00 |
0,00 |
24 a 30 |
0,50 |
1,50 |
0,99 |
0,75 |
0,42 |
0,32 |
0,12 |
0,09 |
0,02 |
0,02 |
30 a 36 |
0,67 |
1,95 |
1,45 |
1,23 |
0,75 |
0,35 |
0,19 |
0,09 |
0,01 |
0,00 |
36 a 42 |
0,22 |
1,94 |
1,68 |
1,58 |
1,06 |
0,50 |
0,26 |
0,14 |
0,02 |
0,05 |
42 a 48 |
0,24 |
1,29 |
2,03 |
1,96 |
1,19 |
0,47 |
0,20 |
0,06 |
0,06 |
0,02 |
48 a 54 |
0,19 |
1,69 |
1,56 |
2,06 |
1,16 |
0,65 |
0,26 |
0,16 |
0,06 |
0,02 |
54 a 60 |
0,05 |
0,94 |
1,44 |
1,91 |
1,09 |
0,74 |
0,18 |
0,12 |
0,05 |
0,03 |
60 a 72 |
0,07 |
0,93 |
2,67 |
3,29 |
1,69 |
0,92 |
0,49 |
0,34 |
0,18 |
0,11 |
72 a 96 |
0,06 |
1,46 |
3,42 |
4,59 |
3,11 |
1,87 |
0,95 |
0,42 |
0,18 |
0,20 |
96 a 120 |
0,14 |
0,64 |
1,67 |
2,15 |
1,39 |
1,23 |
0,84 |
0,20 |
0,18 |
0,16 |
120 a 144 |
0,00 |
0,31 |
0,57 |
1,48 |
0,91 |
0,97 |
0,36 |
0,13 |
0,12 |
0,06 |
144 a 180 |
0,01 |
0,19 |
0,40 |
0,90 |
1,06 |
0,55 |
0,39 |
0,17 |
0,04 |
0,07 |
180 a 240 |
0,01 |
0,05 |
0,21 |
0,52 |
0,75 |
0,33 |
0,19 |
0,17 |
0,07 |
0,08 |
240 a 500 |
0,01 |
0,06 |
0,21 |
0,36 |
0,29 |
0,40 |
0,19 |
0,26 |
0,20 |
0,14 |
500 o más |
0,01 |
0,00 |
0,02 |
0,02 |
0,04 |
0,04 |
0,00 |
0,04 |
0,02 |
0,06 |
Ahora que hemos introducido el modo de operar en modo intuitivo, vamos a formalizarlo de acuerdo con el concepto de escalas de equivalencia y de economías de escala en el hogar. Si lo que nos interesa son las diferencias entre individuos y no entre hogares, para comparar hogares heterogéneos en lo que a su composición se refiere se hace necesario ajustar los ingresos al tamaño del hogar, teniendo en cuenta a) que los ingresos no tienen por qué distribuirse igualitariamente entre los componentes del hogar, b) que las necesidades de los distintos miembros del hogar no tienen por qué ser iguales (por ejemplo, entre componentes de diferentes edades) y c) que pueden existir economías de escala en función del tamaño del hogar (en virtud de las cuales el bienestar obtenido para cada miembro del hogar por una unidad adicional de gasto monetario crezca en función del tamaño del hogar). Para ajustar los ingresos a esta heterogeneidad de los hogares y poder compararlos entre sí se dividen los ingresos del hogar por el tamaño del hogar ajustado, obtenido ponderando el número de miembros del hogar por sus características (por ejemplo, se asigna a los niños un peso menor que a los adultos en la ponderación). La literatura sobre las escalas de equivalencia es variada, aunque lo único que queda claro es que el uso de un determinado tipo de escalas de equivalencia no domina totalmente sobre otro[23]. Quizás precisamente por esto parece imponerse últimamente el método de elevar el tamaño de los hogares a un parámetro θ, donde 0<θ<1, y generalmente se emplea θ=0,5[24]. Así, tendremos
donde Yi será el ingreso del hogar y Ni será el tamaño del hogar. Si θ= 0, xi será el ingreso por hogar, si θ=1 será el ingreso per cápita y si θ=0,5 será el ingreso por adulto equivalente.
De modo que lo dicho antes sobre el modo de operar con los datos de la tabla debe ampliarse para tener en cuenta que dividiremos el ingreso de cada celda bien por el Ni correspondiente bien por (Ni)½.
Aclarado el modo de proceder, queda todavía la más grande dificultad a afrontar en este apartado: no contamos con una tabla como la indicada arriba (que viene a ser una tabla de probabilidades conjuntas) más que para toda España. ¿Podemos realizar estimaciones de las desigualdades per cápita y por adulto equivalente a nivel provincial en estas circunstancias o debemos pararnos al nivel de los hogares? Creemos, como se ha señalado antes, que merece la pena realizar un intento de proyección. Al fin y al cabo, contamos con la distribución de los hogares por intervalos de renta para cada provincia, contamos con la distribución de los hogares en función de su tamaño para cada provincia y contamos con el dato cruzado para el total español. Proponemos aquí un ejercicio de estimación basado en la teoría de la probabilidad.
Si cada porcentaje de las celdas de la tabla representa la probabilidad de hallar (si elegimos de modo aleatorio) un hogar de las características que implica su celda, las sumas (verticales u horizontales) son las probabilidades marginales (con las que contamos para cada provincia). El peso de cada celda sobre el total de todas las celdas que mantienen una característica similar es la probabilidad condicional. Si sumamos todos los porcentajes de hogares unipersonales obtenemos la respectiva probabilidad marginal (la probabilidad de hallar un hogar unipersonal sea cual fuere su nivel de ingresos); el porcentaje de hogares unipersonales del primer intervalo de ingresos sobre el total de hogares unipersonales (en este caso, el 59,2) es lo que se denomina probabilidad condicionada (“la probabilidad de hallar un hogar del primer intervalo de ingresos condicionado a que sea unipersonal). Es decir, si A es la variables ingresos (que puede tomar un valor Ai, con i=1,...n) y B la variable tamaño del hogar (que puede tomar un valor Bj, con j=1,...m), P(Ai∩Bj) es la probabilidad conjunta de Ai y Bj, o la probabilidad de hallar un hogar de tamaño Bj que esté en el intervalo de ingresos Ai (es decir, nuestras “celdas” de la tabla anterior). Si sumamos horizontalmente para un nivel de ingresos i, hallamos la probabilidad marginal de i, P(Ai)=∑nj P(Ai∩Bj) (la probabilidad de hallar un hogar de ingresos i sin importarnos su tamaño). La probabilidad de hallar un hogar de ingreso Ai sabiendo que es de tamaño Bj (o que “hay que elgir entre los de tamaño Bj) es la probabilidad condicionada de Ai a Bj, y se escribe P(Ai│Bj)= P(Ai∩Bj)/ P(Bj)= P(Ai∩Bj)/ ∑ni P(Ai∩Bj).
Ahora bien, si las dos variables en cuestión fueran independientes, la probabilidad conjunta de un evento en este espacio bidimensional (“la probabilidad de hallar un hogar de ingresos X y del tamaño Y”) sería el producto de las dos probabilidades marginales (“la probabilidad marginal de X por la probabilidad marginal de Y”); en otras palabras P(Ai∩Bj)=P(Ai)P(Bj). Pero hemos visto que no es así y, de hecho, se puede operar con la tabla antes señalada, hallar las probabilidades conjuntas suponiendo que los eventos fuesen independientes y se notará una desviación considerable respecto al valor real de numerosos P(Ai∩Bj). Nosotros tenemos las P(Ai) y las P(Bj) para cada provincia y las P(Ai∩Bj) a nivel español. Podríamos utilizar las P(Bj│Ai) estatales para distribuir “horizontalmente” cada porcentaje de hogares en los varios niveles de ingresos entre los diferentes tamaños (las P(Ai)), o hacer lo propio con las P(Ai│Bj) para distribuir “verticalmente” cada porcentaje de hogares en los varios tamaños entre los diferentes niveles de ingresos. Es decir, podemos, por una parte, repartir la proporción de hogares de un determinado intervalo de ingresos entre los diferentes tamaños de hogares suponiendo que para cada provincia la distribución entre tamaños de hogares de cada intervalo de ingresos es igual al total de España. Podemos, por otra parte, hacer lo propio con los hogares: repartir cada proporción provincial de un tamaño de hogar entre los diferentes niveles de ingresos suponiendo que dicha distribución es similar a la española. Cualquiera de las dos opciones tiene inconvenientes: por una parte, utilizamos solamente la mitad de la información de que disponemos (o bien la distribución de los hogares entre sus tamaños o bien entre los intervalos de ingresos); por otra, el repartir cada categoría de este modo puede distorsionar excesivamente a la otra categoría (si repartimos “verticalmente” y después sumamos “horizontalmente” los resultados pueden distar del dato de que dispongamos para la categoría no empleada en el “reparto”, y viceversa). Por estas razones hemos optado por utilizar el método que nos permite capturar el máximo de información disponible posible y distorsionar en mínimo grado las estructuras originales. Procederemos calculando unos factores de elevación de las probabilidades conjuntas del total español respecto al supuesto de probabilidades independientes y aplicaremos dichos factores a los datos provinciales. Formalmente, si P(Ai∩Bj)≠ P(Ai)P(Bj) porque las variables A y B no son independientes, P(Ai∩Bj)/(P(Ai)P(Bj)) nos dará la medida de cuán desviadas están las probabilidades conjuntas bajo supuestos de no independencia y de independencia para cada par Ai y Bj, o de cuanto cabe elevar o disminuir P(Ai)P(Bj) para que proporcione la auténtica probabilidad conjunta; habiendo obtenido estos factores de elevación a nivel español, los aplicaremos a las probabilidades conjuntas bajo supuesto de independencia de las variables a nivel provincial para hallar una aproximación a las auténticas probabilidades conjuntas. Estos factores de elevación captan la relación “orgánica” entre las dos variables no independientes (nos dan la medida de la “no independencia” para cada valor conjunto de las variables), y suponer que esta relación (entre tamaño de los hogares y nivel de ingresos) es igual para toda España es un supuesto mucho menos fuerte que suponer que el tamaño de los hogares no varía o que la distribución en intervalos de ingresos no lo hace (supuestos respectivamente implícitos en el uso de las otras alternativas). Nótese que no estamos suponiendo que la relación entre tamaño de los hogares y el nivel de sus ingresos es constante, sino simplemente la relación entre las respectivas probabilidades marginales (que pueden variar incluso significativamente). El factor de elevación puede ser elevado, pero si la base a la que se aplica a nivel provincial es pequeña (porque hay pocos hogares de los correspondientes tamaño e ingresos) respecto al nivel estatal, la probabilidad conjunta resultante será también reducida (y viceversa). Adicionalmente, habiendo calculado y aplicado a nivel provincial los factores de elevación, los resultados son extraordinariamente positivos: las distorsiones de los datos así generadas son mínimas. Esta opción parece pues la óptima entre las que se encuentran a nuestra disposición, y será la que empleemos para pasar de la distribución de los ingresos entre hogares a la de entre personas u adultos equivalentes, según el método arriba indicado.
Ahora ya hemos clarificado las dificultades a las que cabe enfrentarse antes fuentes del tipo de las que utilizaremos, hemos especificado los instrumentos que utilizaremos para superarlos y las decisiones metodológicas adoptadas. Sólo queda, pues, aplicar nuestras herramientas para obtener una batería de indicadores que nos den una idea de las desigualdades en ingresos en la España de los años ’60 y evaluar los resultados.
La estructura territorial de las desigualdades en ingresos en la España de los años ’60
Medir la desigualdad en ingresos
Procederemos calculando diferentes índices de desigualdad en los ingresos para cada una de las categorías interesadas. En primer lugar obtendremos el índice de Gini, el más popularizado en su uso aunque no exento de problemas. El índice de Gini es igual a la razón entre el área que queda por debajo de la Curva de Lorenz y el área que queda por debajo de una Curva de Lorenz para una distribución de los ingresos totalmente igualitaria (es decir, la bisectriz del diagrama de Lorenz). El índice de Gini captura relativamente bien las diferencias entre los estratos de renta muy elevada y los de renta muy baja, aunque presenta problemas de captación de las desigualdades en ciertas circunstancias. Dos índices de Gini para dos hipotéticas distribuciones de los ingresos captan bien las diferencias en la desigualdad de ambas distribuciones si una curva de Lorenz queda siempre por debajo de la otra, de modo que está claro que la primera distribución es más desigual que la segunda. Sin embargo, cuando dos curvas de Lorenz se cruzan, el índice de Gini no nos sirve para establecer jerarquías entre distribuciones de los ingresos. Si el 20 más pobre tiene el 5 de los ingresos totales y el 30 tiene el 8 en la distribución A, por ejemplo, y, en la distribución B el 20 más pobre tiene el 4 y el 30 el 7 está claro que la distribución A es más igualitaria que la distribución B. Pero si en la distribución C el 20 de la población más pobre dispone de un 4 pero el 30 dispone de un 9 ¿es más igualitaria la distribución A o la distribución C? La pregunta no tiene respuesta objetiva y, como más cosas de las que se suelen explicitar habitualmente en ciencias sociales, depende de los juicios de valor del observador. El índice de Gini, pues, capta relativamente bien las desigualdades entre los estratos superiores e inferiores de renta, pero es relativamente insensible a cambios en la distribución en los niveles extremos. Capta bien las desigualdades entre ricos y pobres pero no las desigualdades entre pobres ni las desigualdades entre ricos. Por otra parte el índice de Gini no presenta la propiedad de descomponibilidad, de manera que es posible hallar el caso en que un país imaginario compuesto por dos provincias vea caer la desigualdad medida por el índice de Gini en ambas pero vea subir el índice de Gini de la distribución agregada de los ingresos. Por esta razón el índice de Gini para el conjunto de España no está vinculado con ningún tipo de media ponderada de los diferentes índices regionales o provinciales, y al tomarlo como referencia debe tenerse en cuenta este fenómeno. Para superar este problema utilizaremos como, complemento del índice de Gini, una batería de índices que entrañan diferentes juicios de valor sobre la distribución de los ingresos. En primer lugar utilizaremos el índice elaborado por Atkinson, definido como
donde μ es el ingreso medio, yi es el ingreso de cada individuo y ε es un parámetro de aversión a la desigualdad que toma valores positivos; contra mayor sea ε, más peso daremos en nuestro indicador a la desigualdad de los estratos que están por debajo del ingreso medio[25]. Simplificando, podemos decir que contra más cercano a cero, mayor peso damos a la desigualdad en los estratos elevados de nuestro índice, y contra más alejado más importancia daremos a la desigualdad “de los pobres”. Piénsese, para facilitar la comprensión del índice, que está construido a partir de una función de bienestar social aditiva, en que la utilidad de los individuos se mide en función de su nivel de ingresos. Para ε=0 la utilidad social es la suma de las utilidades individuales, mientras que para ε>0 se pondera la utilidad de cada individuo en la construcción de la función de bienestar social asignando una ponderación mayor a la utilidad de los individuos relativamente pobres contra más alejados estén del nivel de ingresos medios y menor contra más superen los ingresos medios; al crecer el parámetro de aversión a la desigualdad se asignará ponderaciones todavía mayores a quién esté por debajo del ingreso medio y todavía menores a quién esté por encima. Nosotros calcularemos los índices de Atkinson para parámetros de aversión a la desigualdad de 0,5, de 1 y de 2 para poder capturar las diferencias en los ordenamientos de desigualdad implícitas en diferentes juicios de valor de los mismos. Otra familia de índices que también utilizaremos será la de los índices de entropía generalizada, vinculando la entropía a la dispersión de la información derivada de no tener una distribución de los ingresos totalmente igualitaria. Estos índices toman la forma
y en cierta medida el parámetro de sensibilidad a la desigualdad θ expresa una medida de sensibilidad a la desigualdad, desde el momento en que θ=1-ε en la región en que está definido, de modo que el valor del indicador al crecer el parámetro de sensibilidad a la desigualdad debe interpretarse en sentido inverso al del parámetro del índice de Atkinson. Para valores del parámetro iguales a 1 nos encontramos ante el índice de Theil. Evaluaremos esta función para las diferentes categorías también para tres valores; a saber, θ=0,1,2. Ambas familias de índices, igual que el índice de Gini, ven crecer el valor de sus indicadores para distribuciones de los ingresos más desiguales.
Una vez definidas las formas en que podemos evaluar las desigualdades, procedamos a revisar los resultados obtenidos.
Comenzaremos por un repaso a los índices obtenidos a nivel de las actuales Comunidades Autónomas para los hogares. A continuación presentamos sendas tablas resumen en que se incluyen los distintos índices obtenidos mediante regresión logística de la función de distribución.
Tres comunidades superan el índice de Gini para el conjunto de España: Murcia, Extremadura y Madrid. Asturias y Aragón presentan una desigualdad elevada aunque en ambos casos muy poco inferior a la del conjunto español. Andalucía, Cataluña y Castilla-León presentan resultados algo problemáticos: se mueven entre una desigualdad muy poco inferior a la del conjunto español y una desigualdad medio-alta.
|
Hogares por regresión logística |
||||||
|
Gini |
A(0,5) |
A(1) |
A(2) |
GE(0) |
GE(1) |
GE(2) |
Andalucia |
0,3733 |
0,1170 |
0,2138 |
0,3820 |
0,2405 |
0,2635 |
0,4467 |
Aragon |
0,3890 |
0,1269 |
0,2306 |
0,4090 |
0,2622 |
0,2874 |
0,4934 |
Asturias |
0,3868 |
0,1254 |
0,2282 |
0,4056 |
0,2590 |
0,2831 |
0,4774 |
Baleares |
0,2944 |
0,0723 |
0,1366 |
0,2544 |
0,1468 |
0,1557 |
0,2134 |
Canarias |
0,3514 |
0,1034 |
0,1909 |
0,3456 |
0,2118 |
0,2294 |
0,3602 |
Cantabria |
0,3616 |
0,1095 |
0,2014 |
0,3629 |
0,2250 |
0,2443 |
0,3911 |
Castilla La Mancha |
0,3671 |
0,1131 |
0,2072 |
0,3716 |
0,2322 |
0,2539 |
0,4246 |
Castilla y León |
0,3769 |
0,1193 |
0,2176 |
0,3881 |
0,2454 |
0,2691 |
0,4601 |
Cataluña |
0,3866 |
0,1250 |
0,2279 |
0,4059 |
0,2587 |
0,2811 |
0,4610 |
Extremadura |
0,4182 |
0,1472 |
0,2635 |
0,4584 |
0,3059 |
0,3406 |
0,6513 |
Galicia |
0,3279 |
0,0899 |
0,1676 |
0,3071 |
0,1835 |
0,1974 |
0,2964 |
La rioja |
0,3663 |
0,1124 |
0,2064 |
0,3708 |
0,2311 |
0,2513 |
0,4064 |
Madrid |
0,4299 |
0,1547 |
0,2769 |
0,4813 |
0,3243 |
0,3552 |
0,6346 |
Murcia |
0,3908 |
0,1284 |
0,2327 |
0,4114 |
0,2649 |
0,2928 |
0,5272 |
Navarra |
0,3651 |
0,1116 |
0,2050 |
0,3688 |
0,2294 |
0,2491 |
0,3989 |
País valenciano |
0,3723 |
0,1162 |
0,2127 |
0,3808 |
0,2392 |
0,2609 |
0,4310 |
País vasco |
0,3522 |
0,1038 |
0,1917 |
0,3472 |
0,2128 |
0,2301 |
0,3574 |
España |
0,3904 |
0,1279 |
0,2322 |
0,4114 |
0,2643 |
0,2902 |
0,5037 |
En general, el grado de desigualdad de Cataluña es medio si utilizamos parámetros de aversión a la desigualdad bajos y crece contra más valoremos la desigualdad de los niveles más bajos de renta. Andalucía pasa a presentar parámetros de desigualdad menores a los de Cataluña al asignar más importancia a la desigualdad “entre ricos”. A continuación está Castilla-León, que oscila también en la banda alta de los valores intermedios. Castilla-La Mancha, Canarias y La Rioja presentan valores medio-altos de entre 0,35 y 0,38 en el índice de Gini, junto al País Valenciano. Cantabria, Navarra y País Vasco presentan valores medio-bajos y en ocasiones superan a Canarias. Galicia y Baleares en ambos casos presentan las distribuciones de los ingresos más igualitarias de España. En resumen, por lo menos en lo que respecta a los ingresos de los hogares, parece claro que las distribuciones más desiguales son las de Madrid y Extremadura, seguidas de Murcia, y las más igualitarias las de Baleares y Galicia. El resto de Comunidades fluctúan en un abanico relativamente reducido.
 |
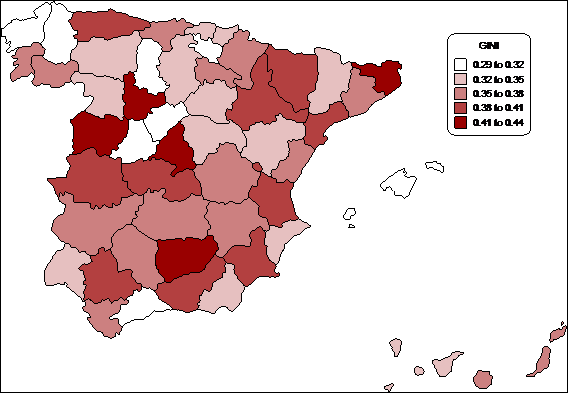
| Figura 3. Índice de entropía generalizada (2) para la distribución de los ingresos de los hogares, comunidades autónomas. |
Queda, pues, mucho por aclarar. Atendiendo a los patrones provinciales de los diferentes índices las diversas tipologías parecen ir conformándose con mucha mayor claridad, así como los desequilibrios intrarregionales que los índices de las CCAA no pueden reflejar. Se confirman las tendencias más claras apuntadas en el análisis regional: Baleares y Galicia presentan niveles de desigualdad reducidos; a estos se suman las provincias septentrionales y orientales de Castilla y León, pero no Valladolid, la provincia más industrializada de la región, ni Salamanca, provincia que se suele englobar en la España del latifundio; Ávila presenta una desigualdad bien superior bien inferior a la de la media, según se mida. La Rioja y las provincias vasco-navarras también tienen índices de desigualdad reducidos, excepto la provincia de Álava. También Asturias se caracteriza por una desigualdad elevada, a pesar de una tipología industrial relativamente similar a la vasca; quizás esto indique ya la decadencia del black country asturiano o, más probablemente, la mejor capacidad de diversificar y reconvertir su economía del País Vasco. En Aragón la provincia de Huesca, ya inmersa en un proceso de despoblación intenso, presenta la mayor desigualdad, pero Teruel (con características similares) presenta unos valores muy reducidos. En todo el tercio nororiental destaca la provincia de Girona, con una desigualdad muy elevada en cualquiera de los índices que tomemos. La desigualdad de la provincia de Barcelona, en contra de lo que cabría esperar dado su elevado crecimiento en estos años y su papel de polo atractivo de la inmigración, no presenta uno de los índices más elevados de desigualdad, a diferencia de Madrid que se mida como se mida es una de las más desiguales de España. Sin embargo, la desigualdad de Barcelona aumenta si aumentamos nuestra sensibilidad a la desigualdad de los ingresos en los tramos altos de renta, al contrario de lo que ocurre en Tarragona, cuya desigualdad es superior a la de Barcelona pero inferior a la gerundense. Cataluña, en general, presenta todas las gradaciones de la desigualdad, puesto que la provincia de Lérida presenta una desigualdad de las más bajas de España. El País Valenciano, con su combinación de industria de medianas dimensiones estructurada en torno a clusters agroindustriales y su agricultura altamente capitalizada, presenta una desigualdad moderada, aunque la provincia de Valencia, con mayor presencia de la gran industria y con los Altos Hornos de Sagunto, si consideramos algunos índices pasa a tener una desigualdad medio-alta. El caso andaluz es significativo; las provincias de Málaga y Almería, de la Andalucía Oriental con mayor peso de la pequeña propiedad, presentan índices reducidos de desigualdad, pero no así la provincia de Granada, que suele agruparse a las otras dos en lo que se refiere a características socio-económicas. La Andalucía del latifundio solo presenta niveles de desigualdad elevados (por este orden) en las provincias de Jaén, en Sevilla y Córdoba, aunque los índices más sensibles a la desigualdad en los niveles bajos la reducen en términos relativos; mientras, Cádiz y Huelva presentan índices más moderados. Extremadura, en cambio, junto a la provincia de Salamanca, sí que sigue las pautas esperadas de alta concentración de la propiedad de la tierra, estructura productiva y ocupacional muy agraria y altos índices de desigualdad. Estimando por regresiones logísticas la desigualdad de las provincias extremeñas se reduce sensiblemente y dejan de ser las más desiguales de España, pasando a ocupar este lugar Madrid. Gerona, Salamanca y Valladolid y Jaén, aunque se sitúan justo por detrás junto a Sevilla. En todo caso, dada la mayor heterogeneidad en las desigualdades de las otras Comunidades Autónomas, la región extremeña sigue siendo la más desigual junto a Madrid y Asturias.
Así pues, la fotografía de la mayor parte de las regiones parece confirmarse mediante el empleo de los dos métodos a nuestra disposición, aunque con matices. Las provincias castellano-leonesas siguen dividiéndose entre Salamanca y Valladolid (las más desiguales) y el resto; Asturias se confirma como el área más desigual del noroeste; el País Vasco, Cantabria, Navarra y La Rioja siguen presentando niveles de desigualdad moderados y Cataluña y Aragón presentan fuertes desequilibrios territoriales, aunque sus niveles de desigualdad en términos relativos disminuyen en relación a la estimación hecha mediante el método del punto medio, pues los niveles de ingresos de sus clases bajas son más elevados que en otras áreas y, subestimándolos, sobreestimábamos su grado de desigualdad. En todo caso permanece la provincia de Girona como una de las más desiguales; el resultado es sorprendente porque, por lo menos en teoría, no debería atribuirse a la escasa representatividad de la muestra, ya que en virtud de su relativamente reducida población la muestra es más representativa. Quizás los problemas muestrales podrían aducirse a la hora de explicar los resultados inesperadamente discordantes de Madrid y Barcelona; sin embargo el hecho de que Madrid era una de las provincias más desiguales de España coincide con la estimación hecha por Ayala, Jurado y Pedraja a partir de la EPF de 1973-1974, en que el diseño de la muestra se hizo ya en modo proporcional a la población.
Cabría suponer que Madrid, en cuanto concentraba una proporción superior de residentes ricos, vinculados al gran capital, a los negocios con el Estado y con las jerarquías del régimen y a grandes burócratas, tenía por esto mayores niveles de desigualdad simplemente por contar (quizás simplemente por razones de residencia desvinculadas de la actividad productiva) con mayor número de perceptores de ingresos elevados. Sin embargo esto no parece confirmarse por nuestros índices, ya que al aumentar la aversión a la desigualdad el alto grado de desigualdad madrileño permanece. En general, donde sí aumenta la medida de la desigualdad al aumentar nuestra aversión a la misma es en el área catalana y aragonesa (marcadamente en las provincias más urbanizadas y que absorbían a más población inmigrante, Barcelona y Zaragoza), reflejando probablemente estos desequilibrios en los estratos más bajos de renta, más moderados para los estratos medio-bajos y superiores. Por contra, las provincias extremeñas, andaluzas y manchegas ven reducirse relativamente su grado de desigualdad (aunque sigue siendo elevado) al aumentar nuestra aversión a la misma, indicando unos desequilibrios mayores entre las rentas altas que en otros lugares; en el sur, los ricos son mucho más ricos que la clase media alta que en otros lugares de España.
 |
| Figura 4. Índice de Gini para la distribución de los ingresos de los hogares, provincias. |
En cambio, en Barcelona y Zaragoza, el lumpenproletariado y el proletariado poco cualificado y de pocos ingresos percibe (relativamente) menos ingresos que el proletariado industrial y de servicios, o que los perceptores de ingresos medio bajos, que en otras áreas industriales como la vasco-navarra o la valenciana, con la excepción de Álava, cuyo dato es muy volátil y quizás no necesariamente significativo.
Andalucía no reproduce más que parcialmente, como se ha comentado, la geografía del latifundio, con provincias occidentales como Cádiz, Huelva y Córdoba (aunque en menor medida) con desigualdades no muy elevadas; por otra parte, Almería y Málaga sí que siguen el patrón andaluz oriental pero la provincia de Granada no.
Pero estos resultados pueden llevar a engaño.
Recuérdese lo dicho sobre el tamaño de los hogares y sobre como éste, en relación con los ingresos, pueden modificar la desigualdad observada. A continuación presentamos simplemente los mapas relativos a los índices de Gini de la distribución del ingreso per cápita y por adulto equivalente; en el Cuadro 4 pueden consultarse los datos completos referidos a esta última categoría. Los resultados son bastante similares al caso de los hogares. Si acaso, el área del latifundio coincide todavía más que en los casos anteriores con los mayores índices de desigualdad, puesto que aumenta la de la provincia de Córdoba y disminuye la de Granada; también aumenta el grado de desigualdad de Cádiz. Tres son las áreas del país que presentan un tamaño medio de los hogares notablemente superior al de la media: el área suroccidental con un foco especialmente intenso en Cádiz, el área vasco-navarra y el área gallega. En el primer caso, al pasar de hogares a individuos o adultos equivalentes, el grado de desigualdad aumenta, lo que indica que hay relativamente más familias pobres numerosas que de tamaño reducido; en los otros dos focos la desigualdad aumenta ligeramente, con el cambio, en el área Pirenaica occidental, aunque no de un modo significativo y permanece en los mismos niveles en el caso gallego.
 |
| Figura 5. Índice de entropía generalizada (2) para la distribución de los ingresos de los hogares, provincias. |
Los principales resultados, pues, de la evaluación que hemos realizado de la desigualdad en los ingresos son los comentados: las áreas más desiguales son Madrid y Extremadura (una de las más ricas provincias de España y dos de las más pobres), junto a parte de Andalucía, la zona meridional de Castilla y León (la latifundista provincia de Salamanca y la industrializada provincia de Valladolid) y la provincia de Gerona (una anomalía para la que no hallamos explicación convincente); las áreas con una distribución del ingreso más igualitarias son Baleares y Galicia (nuevamente, una de las áreas más ricas y una de las más pobres), junto a áreas del norte y este de Castilla y León. Cataluña presenta fuertes contrastes, del mismo modo que Aragón (aunque aquí, como en el caso vasco, son menos acentuados). Navarra, Rioja, Valencia y especialmente la parte oriental de Castilla-La Mancha tienen niveles de desigualdad entre moderados e intermedios. El archipiélago canario parece más desigual en la provincia de Las Palmas que en la de Santa Cruz de Tenerife.
 |
| Figura 6. Índice de Gini para la distribución de los ingresos per cápita, provincias. |
Finalmente, se observa que para mediados de los años ’60 no hay relación entre desigualdad e ingresos, de modo que no se produce ningún efecto tipo Kuznets de ida y vuelta en la relación entre ingreso medio y desigualdad (como tampoco hay relación positiva ni negativa entre ambas variables); sabemos que no es correcto realizar análisis con implicaciones dinámicas a partir de datos de sección cruzada, pero a veces se arguyen argumentos de este tipo para probar relaciones de este tipo; no es así para el caso español en pleno desarrollismo. A continuación se presenta en un gráfico la relación entre el índice de Gini por adulto equivalente y la renta familiar bruta disponible de las familias de cada provincia en 1965, según la estimación realizada por Julio Alcaide[26]. Con cualquiera de los índices elaborados se halla una relación similar.
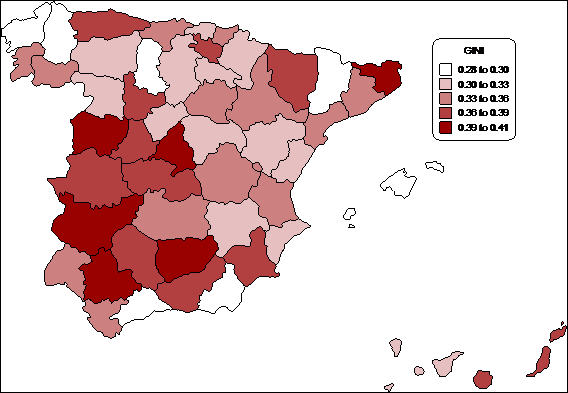 |
Figura 7. Índice de Gini para la distribución de los ingresos por adulto equivalente, provincias. |
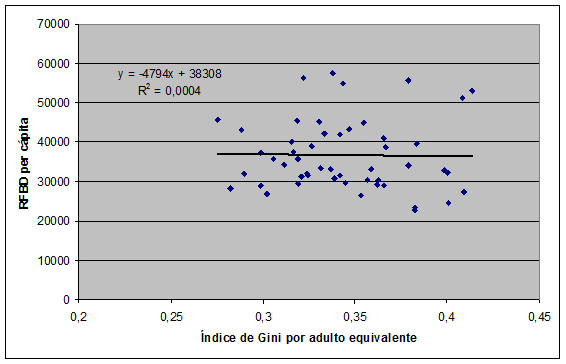 |
| Figura 8. Relación entre ingresos medios y desigualdad de la distribución de los ingresos en España, 1965. |
|
GINI |
A(0,5) |
A(1) |
A(2) |
GE(0) |
GE(1) |
GE(2) |
|
|
Álava |
0,3790 |
0,1172 |
0,2106 |
0,3528 |
0,2364 |
0,2631 |
0,3871 |
|
Albacete |
0,3191 |
0,0881 |
0,1657 |
0,3090 |
0,1811 |
0,1932 |
0,2941 |
|
Alicante |
0,3263 |
0,0902 |
0,1684 |
0,3095 |
0,1844 |
0,1979 |
0,2923 |
|
Almería |
0,3024 |
0,0816 |
0,1499 |
0,2730 |
0,1624 |
0,1834 |
0,2875 |
|
Ávila |
0,3655 |
0,1060 |
0,2014 |
0,3566 |
0,2249 |
0,2221 |
0,2703 |
|
Badajoz |
0,4007 |
0,1355 |
0,2394 |
0,3977 |
0,2737 |
0,3140 |
0,5325 |
|
Baleares |
0,2755 |
0,0659 |
0,1295 |
0,2630 |
0,1387 |
0,1377 |
0,1831 |
|
Barcelona |
0,3432 |
0,0988 |
0,1866 |
0,3527 |
0,2065 |
0,2129 |
0,2875 |
|
Burgos |
0,3165 |
0,0851 |
0,1622 |
0,3052 |
0,1769 |
0,1816 |
0,2398 |
|
Cáceres |
0,3823 |
0,1230 |
0,2216 |
0,3753 |
0,2505 |
0,2800 |
0,4691 |
|
Cádiz |
0,3416 |
0,0947 |
0,1821 |
0,3395 |
0,2010 |
0,1976 |
0,2411 |
|
Castellón |
0,3155 |
0,0856 |
0,1651 |
0,3235 |
0,1804 |
0,1819 |
0,2440 |
|
Ciudad real |
0,3446 |
0,0971 |
0,1865 |
0,3464 |
0,2064 |
0,2032 |
0,2528 |
|
Córdoba |
0,3621 |
0,1155 |
0,2013 |
0,3333 |
0,2248 |
0,2742 |
0,4951 |
|
Cuenca |
0,3568 |
0,1105 |
0,1994 |
0,3470 |
0,2224 |
0,2532 |
0,4344 |
|
Gerona |
0,4084 |
0,1376 |
0,2473 |
0,4198 |
0,2840 |
0,3099 |
0,4687 |
|
Granada |
0,3824 |
0,1214 |
0,2197 |
0,3737 |
0,2481 |
0,2736 |
0,4380 |
|
Guadalajara |
0,3190 |
0,0845 |
0,1677 |
0,3294 |
0,1836 |
0,1714 |
0,1981 |
|
Guipúzcoa |
0,3379 |
0,0950 |
0,1735 |
0,3038 |
0,1905 |
0,2110 |
0,3001 |
|
Huelva |
0,3389 |
0,0975 |
0,1785 |
0,3160 |
0,1967 |
0,2193 |
0,3572 |
|
Huesca |
0,3658 |
0,1147 |
0,2069 |
0,3623 |
0,2318 |
0,2603 |
0,4073 |
|
Jaén |
0,4091 |
0,1489 |
0,2498 |
0,3890 |
0,2875 |
0,3657 |
0,7053 |
|
La coruña |
0,2896 |
0,0695 |
0,1406 |
0,2892 |
0,1516 |
0,1379 |
0,1470 |
|
Las palmas |
0,3791 |
0,1178 |
0,2137 |
0,3652 |
0,2404 |
0,2620 |
0,3770 |
|
León |
0,3116 |
0,0844 |
0,1604 |
0,3052 |
0,1749 |
0,1827 |
0,2689 |
|
Lérida |
0,2884 |
0,0684 |
0,1334 |
0,2640 |
0,1432 |
0,1417 |
0,1665 |
|
Logroño |
0,3304 |
0,0946 |
0,1780 |
0,3343 |
0,1960 |
0,2068 |
0,3056 |
|
Lugo |
0,2823 |
0,0674 |
0,1300 |
0,2518 |
0,1392 |
0,1429 |
0,1919 |
|
Madrid |
0,4137 |
0,1392 |
0,2509 |
0,4223 |
0,2889 |
0,3105 |
0,4518 |
|
Málaga |
0,2986 |
0,0747 |
0,1435 |
0,2749 |
0,1549 |
0,1576 |
0,1988 |
|
Murcia |
0,3629 |
0,1087 |
0,2053 |
0,3711 |
0,2298 |
0,2325 |
0,3101 |
|
Navarra |
0,3188 |
0,0862 |
0,1651 |
0,3195 |
0,1804 |
0,1835 |
0,2443 |
|
Orense |
0,3533 |
0,1089 |
0,1984 |
0,3532 |
0,2211 |
0,2481 |
0,4238 |
|
Oviedo |
0,3666 |
0,1161 |
0,2058 |
0,3486 |
0,2304 |
0,2692 |
0,4493 |
|
Palencia |
0,2989 |
0,0746 |
0,1472 |
0,2905 |
0,1592 |
0,1527 |
0,1805 |
|
Pontevedra |
0,3370 |
0,0966 |
0,1803 |
0,3284 |
0,1988 |
0,2106 |
0,2939 |
|
Salamanca |
0,4003 |
0,1355 |
0,2410 |
0,4035 |
0,2758 |
0,3127 |
0,5385 |
|
Santa Cruz de Tenerife |
0,3246 |
0,0875 |
0,1613 |
0,2868 |
0,1759 |
0,1920 |
0,2654 |
|
Santander |
0,3333 |
0,0962 |
0,1760 |
0,3158 |
0,1935 |
0,2163 |
0,3350 |
|
Segovia |
0,3058 |
0,0799 |
0,1522 |
0,2873 |
0,1652 |
0,1721 |
0,2517 |
|
Sevilla |
0,3986 |
0,1325 |
0,2337 |
0,3848 |
0,2662 |
0,3057 |
0,5014 |
|
Soria |
0,3315 |
0,0904 |
0,1766 |
0,3387 |
0,1943 |
0,1863 |
0,2237 |
|
Tarragona |
0,3550 |
0,1085 |
0,1978 |
0,3505 |
0,2203 |
0,2453 |
0,3972 |
|
Teruel |
0,3209 |
0,0863 |
0,1665 |
0,3174 |
0,1821 |
0,1812 |
0,2302 |
|
Toledo |
0,3589 |
0,1053 |
0,1969 |
0,3505 |
0,2193 |
0,2272 |
0,3046 |
|
Valencia |
0,3421 |
0,0964 |
0,1829 |
0,3385 |
0,2020 |
0,2052 |
0,2640 |
|
Valladolid |
0,3837 |
0,1205 |
0,2274 |
0,4118 |
0,2580 |
0,2571 |
0,3417 |
|
Vizcaya |
0,3220 |
0,0894 |
0,1634 |
0,2942 |
0,1784 |
0,2009 |
0,3097 |
|
Zamora |
0,3239 |
0,0874 |
0,1688 |
0,3185 |
0,1849 |
0,1830 |
0,2312 |
|
Zaragoza |
0,3467 |
0,1023 |
0,1955 |
0,3695 |
0,2175 |
0,2190 |
0,3082 |
|
España |
0,3774 |
0,1191 |
0,2181 |
0,3834 |
0,2460 |
0,2647 |
0,3973 |
Hemos concluido nuestro análisis sobre las desigualdades en los ingresos en los años ’60. Sin embargo, como ya se dijera en la introducción, los ingresos son solamente uno de los varios elementos que permiten evaluar el nivel de vida y, del mismo modo, las desigualdades en los ingresos capturan solamente una parte de las desigualdades en los niveles de vida. A continuación evaluaremos otro elemento determinante del nivel de vida, la alimentación, y estudiaremos su relación con los ingresos monetarios y con su distribución.
Como ya se ha dicho, la Encuesta de Presupuestos Familiares de 1964-1965 ofrece datos sobre el consumo de alimentos. Una gran ventaja de la encuesta es que proporciona información sobre el consumo por persona anual en términos físicos de un amplio rango de alimentos y de su distribución por provincias, de manera que no hay que temer que se entrecrucen precios y cantidades como sucede cuando estudiamos el gasto en cada categoría.
A diferencia de las estimaciones ministeriales o de las de la FAO, la Encuesta de Presupuestos Familiares permite realizar una estimación de las diferencias provinciales en el consumo físico de alimentos; por esto supone una fuente de información de inestimable valor, puesto que mediante las estimaciones de hojas de balance alimentario no tenemos modo de asignar territorialmente los totales nacionales. La otra gran ventaja de la información proporcionada por la EPF es que, a diferencia también de los datos de la FAO y de las estimaciones ministeriales, se incluye el autoconsumo.
Procedamos, pues, habiendo visto ya las características de las fuentes, a analizar las desigualdades en la alimentación en la España de los años ’60.
Desigualdades territoriales en los niveles de nutrientes
El mayor estudio del estado nutritivo de los españoles en este periodo fue realizado por Gregorio Varela[27], uno de los mayores expertos españoles en nutrición del siglo pasado. En “La nutrición de los españoles. Diagnóstico y recomendaciones” Varela utilizaba los datos proporcionados por la Encuesta de Presupuestos Familiares de 1964-65 para realizar una evaluación de los niveles medios de ingesta de diferentes nutrientes para las distintas provincias españolas[28]. El primer hecho relevante es que, según sus datos, no existe una correlación clara entre el mapa de los ingresos medios en España y el mapa de los niveles nutritivos medios para ninguno de los tres tipos de nutrientes principales que consideraremos (calorías, grasas y proteínas). Podría argumentarse que los niveles medios pueden ocultar información (y seguramente lo hagan) y que, para algunas categorías de alimentos (especialmente los de origen animal, cuyo consumo suele asociarse a un incremento en las rentas) los niveles nutritivos medios no hagan más que ocultar severas diferencias entre los distintos perceptores de ingresos (o entre las clases sociales) de una determinada provincia. Si este fuera el caso, las diferencias nutritivas medias deberían mantener alguna relación con alguno de los índices de desigualdad calculados, o con los indicadores de bienestar tipo función de bienestar social de Sen que capturan ingresos medios y niveles de desigualdad. Pero los niveles de calorías, proteínas y grasas medios provinciales no guardan correlación alguna significativa con ninguna de estas variables (regresando todas las variables posibles de las tres categorías de nutrientes con cualquiera de las series de ingresos, indicadores de desigualdad o funciones de bienestar social que podamos construir no se obtiene ningún resultado que alcance un R2 de 0,1). En el caso de las calorías (Figura 9) la agregación geográfica es de difícil interpretación, pues vemos como los mayores niveles se encuentran en la zona cantábrico-gallega (aunque con niveles mínimos en las contiguas provincias castellanas), por una parte, y en un área que va de modo intermitentemente desde las provincias levantinas y su interior, el sistema ibérico, hasta algunas provincias andaluzas. Almería, las provincias valencianas, Galicia y Baleares (áreas en las que la desigualdad es relativamente reducida) mantienen unos niveles relativamente elevados, pero la mayor parte de provincias castellanas, Navarra y las provincias vascas más igualitarias (Guipúzcoa y Vizcaya) mantienen niveles similares a los del área salmantino-extremeña (con niveles de desigualdad máximos), Madrid, las provincias andaluzas más desiguales en ingresos (si exceptuamos Jaén) Granada y Sevilla y las provincias catalanas.
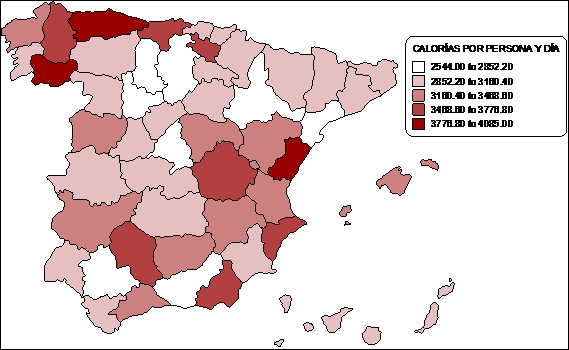 |
| Figura 9. Calorías por persona y día en España. |
El mapa de las proteínas (Figura 10) es en cierto sentido similar al de las calorías, con una localización más clara todavía (y también más reducidas, con mayor homogeneidad en el resto del territorio) de los focos de consumo máximo señalados, y con unos déficits en el consumo especialmente acentuados en el área andaluza y extremeña pero también catalano-aragonesa. Por contra, el consumo de grasas (Figura 11) presenta una compactación al alza de los distintos niveles de consumo: niveles máximos en el cinturón que va desde Badajoz hasta Castellón y Teruel (pasando por el norte de Andalucía y el este manchego) y un eje norte mucho más reducido, con marcados contrastes entre Asturias y Cantabria (con niveles máximos) y las provincias gallegas (con niveles mínimos). En general, el resto del país presenta niveles de consumo situados en el mismo rango.
 |
| Figura 10. Proteínas por persona y día en España. |
Cabe también decir, en general, que la dispersión de los tres elementos considerados es menor que la de los ingresos per cápita provinciales medios (si medimos dicha dispersión por la razón entre la desviación estándar y la media) y también que la mayoría de índices de desigualdad obtenidos en el capítulo anterior[29]. De hecho, según Varela, excepto en los casos de los hogares urbanos de tamaño muy numeroso (superior a los 8 componentes por hogar) los niveles medios de ingesta calórica y de éstos y la mayoría de lo demás nutrientes superaban (en ocasiones de mucho, como las grasas) los niveles mínimos de acuerdo a las escalas establecidas por la FAO aplicadas a la estructura de la población española; en todo caso, se señalaban déficits importantes y generalizados de vitamina A y de riboflamina, y solamente la niancina y el ácido ascórbico se consumía en cantidades correctas para todos los estratos. Hay que notar, sin embargo, que para una serie de nutrientes Varela subestima (dados los conocimientos científicos actuales) los requerimientos mínimos de nutrientes, de modo que en realidad, como puso de manifiesto Cussó[30], para algunos otros tipos de nutrientes los déficits son relevantes en prácticamente todo el país (como el calcio) o en varias regiones (como el hierro en la mitad norte del interior y en Andalucía Occidental). Con todo, el mismo Varela apunta a que los niveles medios no son un indicador totalmente correcto del estado nutritivo, por ocultar determinadas realidades de déficits nutritivos considerables para diversos estratos. Sin embargo, no disponemos de este tipo de información, y nos limitaremos a trabajar en el supuesto de que allá donde los déficits eran más marcados esto se reflejaba en los niveles medios y, si no lo hacía porque los estratos de ingresos más elevados consumían proporcionalmente mucho más, esto debía ser un indicio de altos niveles de desigualdad, que deberían poder ser recogidos por nuestros índices.
 |
| Figura 11. Grasas (lípidos) por persona y día en España. |
De modo que hasta ahora no puede hablarse de una relación clara entre ingresos (y su distribución) y niveles nutritivos. Si los ingresos monetarios y su distribución no nos explican las diferencias nutritivas parece obligado, pues, recurrir a otras variables: en primer lugar la composición misma de la dieta que genera estos niveles de nutrientes agregados y los determinantes de sus respectivas demanda, entre los cuales los precios relativos parecen ser un candidato de primer orden.
Los componentes de la alimentación
Las estructuraciones territoriales de la alimentación
Pasemos pues a un análisis algo más desagregado. Hemos visto como los niveles medios más reducidos de consumo calórico y de ingesta de proteínas y de grasas no se encuentran necesariamente ni en las provincias más pobres ni en las más desiguales, y, viceversa tampoco los niveles más elevados se encuentran necesariamente ni en las áreas más ricas ni en las más igualitarias. Las diferencias, debían deberse a diferentes modos de aprovisionarse de los diferentes nutrientes aún permitiendo cierta interrelación con los niveles y la distribución del ingreso. Veamos, pues, si podemos aclarar algo más atendiendo a la relación entre ingresos y su distribución, precios, estructuras demográfico-sociales (para tener en cuenta que los niveles medios de cada provincia no corresponden a un habitante medio igual) y estructura de la dieta.
En primer lugar, repasemos los alimentos de cuyo consumo anual medio per cápita a nivel provincial disponemos a través de la Encuesta de Presupuestos Familiares. Por una parte tenemos el pan, las pastas, las patatas, el arroz, hortalizas y verduras[31], legumbres[32], naranjas, limones y agrios (excluídas las naranjas), plátanos, “otras frutas frescas”[33], carne de vacuno, carne de lanar, carne de cerdo, carne de pollo y gallina, pescados frescos y congelados[34], huevos, leche fresca de vaca, queso, aceites, azúcar y vinos de pasto.
Analizaremos en primer lugar los patrones de consumo de productos de origen vegetal, que suponían la principal fuente de aprovisionamiento de los nutrientes considerados y de otros de gran importancia nutritiva como las vitaminas, para pasar a continuación a centrar nuestra atención en estudiar el consumo de productos de origen animal, fuente importante de proteínas y que se suele asociar a una elasticidad-renta superior a la de otros alimentos.
El consumo de aceites (muy calórico) es elevado en toda la franja meridional y oriental de la península, que grosso modo coincide con el área de mayor consumo de frutas y hortalizas[35] (fuentes especialmente de vitaminas y otros nutrientes aquí no contemplados). El aceite tiene un alto contenido calórico y por sí solo explica los relativamente elevados consumos calóricos del eje Córdoba-Castellón. El consumo de legumbres (fuente fundamental, dada la estructura del consumo de la época, de proteínas) se vuelve particularmente elevado a medida que avanzamos por la mitad occidental de la península para interrumpirse bruscamente en Galicia, donde volvemos a hallar un consumo particularmente bajo. El consumo de patatas se polariza, por una parte, entre toda el área que va desde el noreste al sur (con niveles de entre 70 y 150 kg anuales per cápita en Cataluña, País Valenciano y Andalucía) y, por otra (de un modo mucho más acentuado) en el noroeste con puntas de 400 kilogramos al año. Esta misma área, sin embargo y contra lo que cabría esperarse dado su aprovechamiento especialmente intenso de la patata como fuente de carbohidratos, también presenta niveles elevados de consumo de pan, junto al ya citado cinturón del interior suroriental que gravita en torno a Cuenca con unos 200 kg anuales. De este modo no puede hablarse de compartimentos estanco en la estructura provincial de la alimentación de origen vegetal, pues si bien tenemos áreas relativamente compactas en el consumo de cada bien, éstas se solapan conformando un mosaico de gradaciones dietéticas con cambios, a medida que nos desplazamos en el espacio, bien graduales en la sustitución de un componente por otro bien de ida y vuelta. Solamente el consumo de arroz se encuentra muy localizado en el área productora del País Valenciano y de la provincia de Tarragona. No hay fronteras en la distribución del consumo de los alimentos analizados hasta el momento, y la misma tiene poco que ver con la geografía de los ingresos y de su distribución. Pero no hemos pasado revista todavía al componente más significativo de lo que ha venido en denominarse transición nutricional: los alimentos de origen animal, que revisten un papel cualitativamente muy importante en el análisis de las variaciones territoriales de las dietas. Y aquí, veremos, el mosaico empieza a desaparecer y las fracturas se convierten en más acentuadas, fracturas que, repetimos, tienen una importancia cualitativa mucho mayor a la hora de evaluar cuán avanzada estaba en cada sección del territorio dicha transición nutricional.
De hecho suele argumentares que el incremento de los niveles de renta lleva asociados unos incrementos de productos cárnicos y derivados animales; este mecanismo es uno de los que están a la raíz del actual incremento de los precios mundiales de los alimentos, no solamente porque países enormes como China e India están incrementando sus demandas de estos tipos de productos, sino porque esto genera unos efectos de arrastre hacia atrás en los mercados de piensos que presionan (dada la naturaleza limitada de la tierra cultivable) sobre todos los otros productos agrarios. En una escala más modesta, como ponen en evidencia Rodríguez Artalejo, Banegas, Graciani, Hernández vecino y Rey Calero (1996) el elemento distintivo en el cambio de la dieta de los españoles desde 1940 hasta principios de los años ’90 fue el incremento espectacular de productos cárnicos (junto al de los aceites) que llevó aparejado no solamente el incremento de la ingesta proteica sino el crecimiento espectacular de los lípidos (con las consabidas consecuencias sobre las probabilidades de sufrir enfermedades cardiovasculares: no siempre más es mejor); simétricamente, Cussó y Garrabou (2007) han puesto de manifiesto como este proceso se ha visto acompañado no solamente con un descenso relativo del peso de los cereales, tubérculos y legumbres en las aportaciones nutritivas sino también por una caída en términos absolutos (por cuanto menor que en términos porcentuales). Estas transformaciones en la dieta (particularmente el aumento en la ingesta de nutrientes de origen animal y en aceites vegetales distintos al de oliva) se aceleran notablemente (o incluso se inician, según el tipo de alimento) precisamente en los años ’60. Parece razonable, pues, asociar estas transformaciones del largo plazo por una parte a la aceleración de la tasa de crecimiento de la renta per cápita y, por otra, a las transformaciones en la estructura económica y social que a ella han ido aparejadas, como las implicaciones sobre los hábitos de la sociedad urbana moderna, la disponibilidad de tiempo y los patrones de urbanismo y desplazamientos diarios y, finalmente, el proceso (ya altamente avanzado) de lo que ha venido en llamarse “macdonalización” de los hábitos alimentarios. Pero ¿Podemos cuantificar y territorializar cuán avanzado estaba este proceso a mediados de los ’50? ¿Pueden aplicarse las tendencias a largo plazo para explicar una fotografía fija del corto plazo? ¿Son aquellas secciones del territorio más avanzadas en la convulsión de las estructuras económicas más tradicionales también aquellas que aparentan niveles mayores de consumo de productos de origen animal? Procedamos.
“El país de la carne”
Veamos, en primer lugar, como se distribuía el consumo de alimentos de origen animal y de las aportaciones en términos calóricos y de proteínas y grasas que su consumo suponía. Para ello transformaremos el consumo provincial de cada alimento respectivamente en calorías, proteínas y grasas mediante los coeficientes utilizados en las Hojas de Balance de Alimentos de la FAO para España para los años en cuestión.[36]. Procediendo de tal modo y agregando, podemos captar un desequilibrio territorial en la alimentación que había quedado oculto por los mapas anteriores.
La ingesta de calorías, proteínas y grasas de origen animal, cuyas particularidades físicas y químicas le confieren un valor diferenciado de la de las de origen vegetal (en cuanto, por ejemplo, implican también un aporte de otro tipo de nutrientes), parece seguir un patrón un tanto diferente respecto a las categorías previamente consideradas.
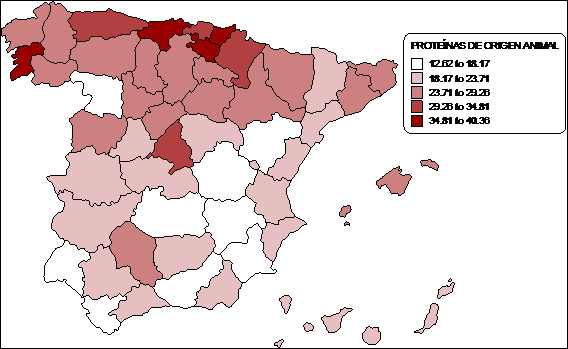 |
| Figura 12. Proteínas de origen animal: el “país de la carne”, kg por persona y año. |
La relación entre ingresos per cápita e ingesta de calorías y nutrientes de origen animal es ahora significativa (especialmente en el modo de procurarse las proteínas, independientemente de su nivel[37]), con unos R2 de entre 0,3 y 0,5, pero no tanto como cabría esperarse; de modo que la relación, si bien significativa, es suficientemente reducida como para no suponer que otros elementos están actuando; particularmente, la renta puede explicarnos bien las diferencias en los extremos, es decir entre las provincias muy ricas y las muy pobres (que son las que dan pendiente positiva a las rectas y significatividad estadística entre las variables) pero no nos explican las diferencias entre el 80 de provincias restantes; si quitamos los extremos, no hallamos relaciones significativas.
Por esta razón, seguimos hallando anomalías significativas: provincias como las valencianas y Tarragona (que se encuentran en la franja alta de ingresos per cápita) presentan niveles de consumo de productos animales relativamente reducidos, mientras otras más pobres y con estructuras socioeconómicas todavía fuertemente agrarias (las gallegas y castellanas) presentan niveles relativamente elevados.
Por otra parte, la desigualdad en la distribución de dichos ingresos sigue sin ser un factor explicativo. Así pues, los ingresos medios no lo explican todo: la intensidad en el consumo de nutrientes de origen animal parece seguir un gradiente descendente norte-sur; un norte donde hay provincias ricas y provincias pobres; adicionalmente, las provincias del País Valenciano (con niveles de renta relativamente elevados) destacan por unos niveles netamente reducidos.
Hallamos pues un mapa por una parte claro y por otra ambiguo del consumo de alimentos de origen animal. Claro en la medida en que este “país de la carne” está claramente delimitado geográficamente y es bastante homogéneo, y presenta alguna relación (por cuanto de menor intensidad de lo esperado) con los niveles de ingresos; ambiguo en la medida en que no es tan homogéneo atendiendo a estructuras económicas y sociales y tampoco podemos establecer un patrón común de la ingesta de nutrientes de origen animal entre las provincias con mayores niveles de renta.
Parece necesario, pues, intentar explicar mejor este patrón de consumo. Para ello pasaremos a estudiar el consumo de productos de origen animal de forma más desagregada, estimaremos las respectivas ecuaciones de demanda e intentaremos ver cuales son sus determinantes y como interactúan entre sí.
Observando el consumo de carnes podemos reconocer un patrón de consumo ya visto al analizar los nutrientes de origen animal: las provincias con mayores niveles de consumo son todas las de la franja norte (exceptuando la provincia de Zamora). Si atendemos a categorías más desagregadas es fácil verificar como esta homogeneidad septentrional del consumo de carnes desaparece en lo que parece ser una clara fragmentación geográfica de las áreas de consumo; el “país de la carne” parece contar con diferentes provincias igualmente bien delimitadas. Por una parte tenemos el consumo de carne de vacuno concentrado en el litoral cantábrico y Castilla y León (especialmente en su zona occidental), así como en las ricas provincias de Madrid y Barcelona. El consumo más elevado de cordero y otras especies de lanar se concentra entorno a Aragón y las provincias castellanas orientales (junto a las provincias adyacentes de Lérida, Castellón y Navarra). El consumo de cerdo parece ser un componente fundamental en la aportación de nutrientes de origen animal en Galicia, con presencia también (aunque mucho menor) en el norte de Cataluña (Gerona es la única provincia no gallega que supera el consumo de 4 kg anuales). El consumo de pollos es característico de toda la zona levantina (Cataluña, País Valenciano y Baleares). Podría, así decirse, simplificando en exceso, que a medida que vamos del oeste al este hallamos intensidades relativamente fuertes en el consumo de, respectivamente, cerdo, vacuno, cordero y pollo.
Por lo que se refiere al consumo de otros productos de origen animal, el consumo de leche es más elevado en la misma área en la que lo es el consumo de vacuno (confirmando quizás lo dicho antes sobre el autoconsumo, puesto que en Madrid y Barcelona, donde las posibilidades de autoconsumir leche serían más reducidas que en las áreas rurales del Cantábrico, el consumo de leche es comparativamente más reducido que el consumo de carne de vacuno). Pero el consumo de queso no reproduce exactamente el área más consumidora de leche: se sitúa en las islas y en el área suroriental de la península (así como en Badajoz). Del mismo modo, el área en que el consumo de huevos es más elevado tampoco es el área en que se consume más pollo, situándose en el área comprendida entre Aragón y las provincias castellanoleonesas orientales. En el caso del pollo y de los huevos esto puede deberse a la mayor presencia de la pequeña propiedad y al autoconsumo (que representa cerca de una cuarta parte del consumo nacional) consiguiente en relación a las áreas más urbanizadas e industrializadas del levante, que en estos años empezaba (gracias a la introducción de antibióticos) la producción en masa de volatería; el pequeño propietario amortizaba los pollos y gallinas dándole una vida útil más larga a través de su empleo en la producción de huevos. El consumo de pescado más elevado se localiza en las áreas costeras del suroeste y el noroeste y en sus respectivos hinterlands, así como en las grandes áreas urbanas de Barcelona y Madrid y en toda la ruta que une esta última ciudad con los puertos del mar Cantábrico.
Adicionalmente, hay que señalar que la relación entre ingresos y consumo de nutrientes animales es mucho más significativa si atendemos al conjunto de los nutrientes de origen animal que si tomamos los nutrientes de cada producto individualmente.
Una exploración por el “país de la carne”
Para explicar estos patrones de consumo parecería razonable suponer que, teniendo en cuenta las diferencias de ingresos, las diferencias de precios relativos de los diferentes productos animales lleven a las distintas poblaciones a proveerse con más intensidad de proteínas y otros nutrientes animales de aquellos productos en cuya producción cada área tiene una ventaja comparativa. Es decir, en Galicia el consumo de cerdo es tan elevado porque las condiciones ambientales permiten su producción a menor coste relativo que en otras áreas, y así sucesivamente. Niveles similares de ingesta de nutrientes de origen animal son alcanzados en toda la zona norte con estructuras dietéticas bastante diferentes. Este razonamiento implica que las elasticidades precio cruzadas de la demanda de un producto animal en relación a los otros debería ser significativa. Para testar este extremo, hemos regresado el consumo de cada uno de los alimentos en cuestión sobre a) el nivel de ingresos, b) el precio del producto, c) el precio de los productos competidores susceptibles de afectar a la demanda del bien en cuestión (hemos incluido aquí no solamente los productos animales mencionados sino también los huevos, el queso, la leche, el pescado y la legumbre, otra fuente de proteínas), d) el porcentaje de menores de 14 años (para controlar por la estructura por edad[38]) e) el índice de Gini por adulto equivalente para controlar por la distribución de los ingresos.
Los resultados obtenidos son sorprendentes. Hemos procedido del siguiente modo: en principio hemos realizado una estimación con todas las variables indicadas. A continuación hemos procedido a eliminar las variables menos significativas hasta hallar el modelo definitivo (en caso de haberlo).
En el caso del consumo de vacuno, no se ha hallado relación con el precio de ninguna otra de las carnes que podríamos, a priori, suponer influyen en el consumo del mismo. Se ha hallado una relación positiva y significativa con el nivel de ingresos y también con el precio de los huevos (con un coeficiente positivo), de modo que la elasticidad de substitución en el caso de la carne de vacuno no estaría cruzada con otras carnes sino con los huevos: contra más caro el precio de los huevos en relación al de la carne mayor es el consumo de carne, y viceversa. El precio de la carne de vacuno mismo, por otra parte, solo puede considerarse significativo a duras penas. Por otra parte existe una relación negativa con el precio de la leche (a igual precio de la carne, un precio mayor de la leche se asocia con un consumo menor de carne), quizás reforzando la idea de que a mayor precio de la leche (en relación al de la carne de vacuno) aumentaba el ganado destinado a producir leche para el mercado en cambio de carne para su consumo, o mejor dicho el uso que se daba al ganado (para producción cárnica o para producción lechera) en cada zona podía depender del precio relativo de los dos outputs posibles; acaso esto pueda indicar todavía insuficiencias en la integración del mercado (porque indica una gran atención de los productores locales a la demanda local).
La regresión del consumo de carne de lanar presenta resultados estadísticamente más débiles. Está negativamente relacionado con el precio de los huevos y de modo muy significativo (a mayores precios de los huevos, menor consumo de cordero), en lo que quizás sea una coincidencia estadística puesto que el mayor consumo de ambos alimentos coincide geográficamente. Por otra parte, presenta elasticidades de substitución positivas con el precio de la carne de cerdo y con el de las legumbres. Nuevamente el precio mismo de la carne de lanar es significativo solo rozando lo estadísticamente admisible, aunque el coeficiente es del signo esperado.
El consumo de cerdo no puede explicarse con ninguna variable más que por la proporción de jóvenes en la población, reflejando el envejecimiento relativo de la población gallega (y especialmente de las provincias más rurales y más consumidoras de porcino, que cuentan con las menores proporciones de jóvenes en la población del país), cuyo enorme consumo de carne de cerdo en relación al de todas las demás provincias pueda generar resultados distorsionados. De hecho, quitando la variable que nos controla por la estructura por edades de la población no se halla correlación con ninguna otra.
El consumo de carne de pollo y gallina está positivamente relacionada (y en modo muy significativo, estimando cada una de las variables por separado y en distintas combinaciones) con el precio del pescado y de la leche, indicando tal vez cierta sustituibilidad entre las demandas de estos productos. Por otra parte también presenta un coeficiente positivo y significativo la variable ingresos.
Sin embargo, el consumo de pescado no está relacionado con los precios del pollo, pero sí (en el sentido esperado) con los precios de los huevos; los ingresos también están positivamente relacionados con el consumo de pescado, aunque la variable más significativa es el precio.
El consumo de huevos presenta las relaciones predecibles con su propio precio (negativa) y con los ingresos (positiva); presenta elasticidad de sustitución con las legumbres, viéndose su consumo aumentado en presencia de precios de las legumbres más elevados; finalmente, confirmando alguna de las relaciones más inesperadas antes indicadas, está negativamente relacionado con el precio del pescado y del cordero (ante precios más elevados del pescado y del lanar el consumo de huevos es menor).
El consumo de leche es uno de los que queda mejor explicado y que presenta relaciones más complejas. Está positivamente relacionado con los ingresos aunque sorprendentemente está negativamente relacionado con el peso de niños y jóvenes en la población; su precio es muy significativo a la hora de explicar su consumo y éste también está positivamente relacionado con el precio de los huevos de un modo estadísticamente muy significativo. Finalmente, está negativamente relacionado con el precio de la carne de vacuno, lo que parece confirmar nuestra hipótesis sobre tal relación apuntada arriba. También está relacionado negativamente con el precio del pollo, en un resultado altamente sorprendente tras haber hallado una relación inversa entre el consumo de leche y el precio del pollo. Se consume más pollo allá donde la leche es relativamente más cara, pero se consume menos leche allá donde el pollo es más caro. Estos resulta dos son aparentemente inconsistentes, aunque ambas variables son estadísticamente muy significativas en las respectivas regresiones. Quizá la explicación pueda hallarse en los bajos niveles de consumo de pollo: en la mayor parte del territorio no se superan los 3 kg per cápita anuales y allá donde el consumo es muy reducido parece haber margen para el incremento ante precios elevados de la leche; sin embargo los niveles medios de consumo de leche parecen más elevados (al margen de la concentración geográfica de las provincias con consumo per cápita más acentuado), y precios más elevados del pollo pueden conducir a destinar parte de los recursos destinados al consumo de leche a satisfacer unas raciones mínimas de carne de pollo. Una demanda relativamente inelástica de carne de pollo (pero no de la curva de demanda de la leche) explicaría el comportamiento aparentemente sorprendente de los coeficientes. Esta intuición parece verse confirmada por el hecho de que el precio de la volatería no se muestra correlacionado con sus niveles de consumo.
Finalmente, el consumo de queso está negativamente relacionado con su precio, no presenta relación alguna con el precio de la leche, aunque quizás la relación con esta se pueda explicar a través de un coeficiente negativo de la variable ingresos. Al crecer los ingresos, el consumo de los nutrientes (el calcio en primer lugar) asociados a la leche pasaba a realizarse a través de la leche y no ya del queso, cuyos mercados parecen bastante segmentados (quizás debido a la especialización relativa en quesos de oveja y de cabra de la producción quesera española). Las provincias ricas se proveían relativamente más de leche de vaca para los aportes de calcio de los lácteos mientras las más pobres lo hacían con queso (en gran parte, cabe suponer, de oveja). Por otra parte las poblaciones con más niños y jóvenes sí que consumían más queso que las más viejas, de modo que buena parte de la ingesta de los nutrientes de la leche por parte de niños y jóvenes se producía a través del queso. Por otra parte, presenta elasticidades de sustitución con el pescado y con la carne de lanar (quizás en un mecanismo, en este último caso, similar al descrito anteriormente en relación al vacuno y a la leche).
Resumimos a continuación en un cuadro las relaciones halladas y los coeficientes estimados. El cuadro se lee del siguiente modo: un incremento de una unidad en el precio de los alimentos de las distintas filas afecta al consumo del alimento de la columna correspondiente en la medida en que indica el coeficiente correspondiente. Así, un incremento de una peseta en el precio de un kilogramo de vacuno implica un descenso del consumo de carne de vacuno de 0,57 kilogramos anuales y un descenso del consumo de leche de 0,46 litros anuales. Precios del cerdo una peseta más elevados están asociados a niveles de consumo de carne de lanar superiores en 0,36 kilogramos anuales, y así sucesivamente. Las celdas vacías indican que no se halla relación alguna entre el precio de un bien y la cantidad consumida del bien correspondiente. Para una correcta interpretación téngase en cuenta que todos los productos están expresados en kilogramos excepto los huevos, expresados en unidades, cuyo precio unitario rondaba las dos pesetas (de modo que un incremento de una peseta en su precio es muy elevado).
Q vacuno |
Q lanar |
Q cerdo |
Q pollo |
Q pescado |
Q huevos |
Q leche |
Q queso |
|
P vacuno |
-0,57 |
-0,46 |
||||||
P lanar |
-0,19 |
-0,42 |
0,14 |
|||||
P cerdo |
0,36 |
|||||||
P pollo |
-0,58 |
|||||||
P pescado |
0,18 |
-0,75 |
-3,09 |
0,68 |
||||
P huevos |
5,63 |
-9,7 |
12,78 |
-94,39 |
76,33 |
|||
P leche |
-0,29 |
0,26 |
-4,87 |
|||||
P queso |
-0,18 |
|||||||
P legumbres |
0,38 |
5,83 |
¿Qué conclusiones podemos sacar? En primer lugar podemos explicar poco los patrones geográficos de consumo de las distintas tipologías de carnes (vacuno, lanar, cerdo y pollo) en función de sus respectivos precios relativos (el cuadrante superior e izquierdo es el más vacío de coeficientes cruzados). Solamente el precio del cerdo parece afectar al consumo de cordero. En segundo lugar los ajustes en la obtención de proteínas y nutrientes animales en función de su precio suceden solamente en relación con los otros tipos de alimentos de origen animal, como los huevos, la leche, el queso o el pescado. Finalmente, las relaciones entre las distintas estructuras de consumo parecen más complejas de lo que a priori podría decirse. El precio mismo del bien es relevante a la hora de explicar la cantidad consumida en seis ocasiones (vacuno, lanar, pescado, huevos, leche y queso, si bien en las dos primeras el resultado es estadísticamente débil), siendo el consumo de carne de cerdo y de pollo insensible a su propio precio. Estas dos carnes son precisamente los productos de origen animal con mayores tasas de autoconsumo; aunque no conocemos la distribución regional del autoconsumo, podemos conjeturar que el papel de esta realidad económica a la hora de explicar los consumos de alimentos (al margen del mecanismo de la renta y de los precios) fue cualquier cosa menos irrelevante; de hecho, los mayores niveles de consumo de carne porcina se sitúan en el área gallega, con especial intensidad en las provincias más rurales de Galicia (Lugo y Orense), donde la estructura eminentemente agraria de la actividad económica, la subsistencia del minifundio y de la fragmentación de la propiedad constituyen el caldo de cultivo apropiado para el mantenimiento en el tiempo de fenómenos económicamente relevantes de autoconsumo; las mismas características (aunque probablemente algo menos acentuadas) se dan en el área castellanoleonesa oriental (en torno a la provincia de Soria), el foco (aunque con niveles harto más reducidos) de consumo de porcino, junto a las provincias de Gerona y Barcelona (que cuentan con los centros productores tradicionales de Olot y Vic).
La mayor parte de relaciones cruzadas se dan entre el pescado, los huevos y el queso o bien entre éstos y las carnes, pero no entre estas últimas. Dejando de lado los coeficientes negativos, cuya interpretación se ha visto que es problemática, el consumo de carne de vacuno se ve afectado por el precio de los huevos; la carne de cerdo por el precio del lanar y de las legumbres; la carne de cerdo no puede explicarse por ninguna variable; la carne de pollo es sensible a las variaciones del precio del pescado y de la leche. Por otra parte, el pescado es sensible al precio de los huevos, los huevos al precio de las legumbres, la leche al precio de los huevos y el queso al precio del lanar y del pescado. Leche, huevos, pescado y queso se ven involucrados en la mayor parte de relaciones de sustitución, relaciones de no fácil análisis porque la mayor parte de las veces son unidireccionales, indicando unas rigideces de la demanda en relación a unos productos pero no a otros. Se puede consumir más pollo si el pescado es más caro, pero esto no implica que se deje de consumir pescado si el pollo es más barato.
Nótese, finalmente, que la mayor parte de las aportaciones de nutrientes de origen animal las realizan la leche y el pescado; las carnes suponen solamente una tercera parte del consumo de proteínas animales a nivel nacional. Creemos que esto está relacionado con el hecho de que la demanda de carnes parezca bastante menos elástica tanto con respecto a su propio precio como en relación al precio de otros productos.
|
Calorías |
Proteínas |
Grasas |
Carnes |
24,78 |
29,34 |
29,08 |
Huevos |
12,59 |
13,36 |
15,24 |
Leche |
43,80 |
28,80 |
42,22 |
Quesos |
8,52 |
5,60 |
8,21 |
Pescado |
10,30 |
22,90 |
5,26 |
Total |
100,00 |
100,00 |
100,00 |
Los elementos estructurantes del consumo de nutrientes de origen animal no son las carnes; el consumo de éstas se ajusta o bien en función de los precios de los productos competidores (en el caso de la carne de vacuno y la carne de lanar) o bien en función de factores no vinculados a la circulación mercantil. Suponemos que el autoconsumo vinculado con la pequeña propiedad puede ser una causa importante de la escasa relación del consumo de algunos productos (como el cerdo o el pollo) con el sistema de precios en unos casos pero sí en otros. En las zonas de autoconsumo el precio de los productos competidores puede no influir en las decisiones de consumo, pero sí en los centros urbanos. Esto explicaría porqué el precio de algunos productos influye sobre la demanda de terceros productos pero no viceversa. De hecho, atendiendo a los porcentajes de autoconsumo nacionales, el 14 de las calorías de origen animal, el 11 de las proteínas y el 14,7 de las grasas se obtendrían mediante el autoconsumo. Si tenemos en cuenta que tanto los niveles de ingesta de nutrientes de origen animal como (verosímilmente) la tasa de autoconsumo habría sido muy superior en el norte que en el sur la relevancia del fenómeno y su interferencia con el mecanismo de los precios, todavía a la altura de los años ’60, debería ser tenida muy en cuenta.
Conclusiones
Hemos verificado, por una parte, que no existe relación entre los niveles de ingresos y los niveles de calorías, proteínas y grasas de las distintas áreas del país. Hemos verificado que los niveles de las mismas categorías de origen animal, en cambio, sí que se ven relacionados con los ingresos aunque de una manera relativamente débil. Al desagregar por productos, hallamos unos patrones geográficos de consumo muy definidos. Sin embargo, estos mismos patrones solo pueden explicarse parcialmente con los precios y la renta; esto refleja demandas de algunos productos relativamente insensibles a los cambios en la renta y los precios, probablemente vinculadas tanto a tradiciones dietéticas asociadas a sistemas de precios anteriores en el tiempo como a estructuras de aprovisionamiento de los nutrientes de origen animal al margen del mercado (el autoconsumo); de este modo, el proceso de transición alimentaria asociado al incremento de productos de origen animal se encuentra a mediados de los ’60 mucho más avanzado en el norte del país que en el sur, aunque por razones diferentes en las distintas secciones del mismo norte; en algunos casos (Madrid y Barcelona especialmente) puede vincularse al proceso de transformación económica, en otros debe vincularse más a la persistencia de la pequeña propiedad en sociedades agrarias. La confluencia de ambos fenómenos interfiere a la hora de explicar los distintos patrones de consumo por variables monetarias.
En el presente apartado pasaremos a realizar una nueva evaluación de la huella ecológica de la alimentación española en 1965, diferente (y creemos, al menos en la medida en que puede desagregarse territorialmente, más completa) que la realizada por Óscar Carpintero (aunque esté basada en su aportación fundamental) que permita evaluar como se repartía a nivel provincial.
En los años ’60 empieza a funcionar a todo ritmo el modelo económico desarrollista, con todas sus implicaciones. Hoy en día, cuando parece que el desarrollismo (y el acceso a una dieta rica en proteínas animales) se ha extendido a millones de personas del tercer mundo, a las que les son presentados como el mejor y único modelo de sociedad deseable, este aspecto parece especialmente relevante. En cierto sentido, estamos asistiendo a un proceso como el vivido por España en los años ’60 y primeros ’70 reproducido a escala mundial, y en términos ecológicos, como se hace evidente día a día, la escala cuenta. Esto es cierto no solo para los procesos de apropiación (directa o indirecta) del espacio vinculados a los cambios de uso del territorio, a la urbanización, al incremento de los consumos energéticos, al despilfarro de recursos, a los volúmenes crecientes de desperdicios que la actividad económica devuelve al medioambiente. Lo es también, en un terreno más básico, para uno de los procesos esenciales para el mantenimiento de la vida humana, cuyas complejas pautas hemos analizado arriba: la alimentación.
Pasemos pues a estudiar este tipo de procesos en nuestro “microuniverso” español de los años ’60.
Podemos calcular la huella ecológica de la alimentación a nivel provincial gracias a, por un lado, la citada Encuesta de Presupuestos Familiares y, por otro, a la fundamental contribución de Óscar Carpintero en “El metabolismo de la economía española. Recursos naturales y huella ecológica (1955-2000)” (2005), en la que construye la huella ecológica de la economía española desde 1955. En ella se sientan las bases de unas series de contabilidad ecológica para España exhaustivas, y son una fuente inestimable. Sin embargo, en algunas rúbricas, pueden ser mejoradas y completadas. Una de ellas es precisamente la de la huella ecológica de la alimentación. De hecho, se verifican diferencias importantes entre los datos utilizados por Carpintero y los ofrecidos por otras fuentes, como por ejemplo los de la Encuesta de Presupuestos Familiares. Veamos en detalle estas diferencias y como podemos interpretarlas.
La diferencia más grande se refiere a los datos de consumo de alimentos por habitante que utiliza Carpintero. La razón principal, según se desprende de la información contenida en el Anexo Metodológico de su libro, parece residir en el hecho de que ha privilegiado una aproximación por el lado de los inputs antes que por el lado de los ouputs. El enfoque es correcto si de lo que se trata es de calcular la ocupación de espacio que se utiliza para la producción de un determinado alimento; sin embargo, no tiene en cuenta algunos elementos, como que pueden darse pérdidas o despilfarros en los alimentos consumidos. En otras palabras, el enfoque de tomar las producciones es correcto para calcular los coeficientes de huella ecológica unitaria (los requerimientos territoriales de la producción de una unidad, generalmente kilogramos o litros, del alimento en cuestión); si queremos, en cambio, atender a la huella ecológica de la alimentación (los requerimientos territoriales de las unidades de alimentos efectivamente consumidas), debemos en cambio aplicar dichos coeficientes a los consumos efectivos de los alimentos y no a los volúmenes de su producción. Las pérdidas deben detraerse, del mismo modo que se debería hacer con las exportaciones ocultas, mientras que la producción oculta debería sumarse. Las pérdidas no son propiamente huella ecológica de la alimentación, aunque lo son del sistema agroalimentario. Del mismo modo, las exportaciones ocultas no son huella ecológica de la alimentación española, sino de aquellos países a los que se destina. Discurso inverso vale otra vez para la producción oculta. Hay que diferenciar entre la huella ecológica de la agricultura (o mejor del sistema agroalimentario, puesto que si las pérdidas son atribuibles al circuito de comercialización no está claro que deban asignarse a la agricultura) y la de la alimentación.
Pero, ¿por qué deberían ser más fiables los datos de la Encuesta de Presupuestos familiares que los utilizados por Carpintero? En primer lugar ante una encuesta de este tipo no había incentivo alguno a mentir sobre los consumos, a diferencia de lo que ocurría con los ingresos. En cambio, las estadísticas realizadas por el ministerio del ramo eran vistas siempre por los productores como susceptibles de ser utilizadas con fines tributarios: aquí los alimentos son su producción, y no su consumo como en el caso de los hogares.
En segundo lugar, los datos de la encuesta están elaborados tanto con la producción comprada en el mercado como con el autoconsumo, categoría de la que los datos del MAPA carecían.
Al margen de estas consideraciones, el uso de los datos de consumo de la Encuesta de Presupuestos es el único que nos permite desagregar territorialmente la huella ecológica de la alimentación española.
Si lo que queremos es captar las diferencias en la distribución de la huella ecológica de la alimentación, hay pues que aplicar los coeficientes calculados por Carpintero a las categorías desagregadas de alimentos.
Esta última operación entraña ciertas dificultades.
En primer lugar, hay que hacer comparables temporalmente los datos de Carpintero y los de la Encuesta. Para ello hay que transformar los datos de kilogramos por habitante y (más importante) la huella ecológica unitaria (metros cuadrados por kilogramo, que serán los coeficientes que utilicemos para calcular la huellas ecológicas provinciales). Intrapolando las tasas de crecimiento anual acumulativas para los datos de hectáreas por habitante de cada categoría a partir de los datos de 1961 y 1975 y después aplicar dichas tasas hasta obtener el valor correspondiente a 1965 (cogeremos este año como año de referencia de la EPF para simplificar) es la opción más evidente.
El siguiente obstáculo que debemos superar es la homologación de categorías alimenticias. Con la EPF tenemos datos detallados a nivel provincial para las categorías citadas en el apartado anterior. Los coeficientes de huella ecológica por kilogramo de alimento y los kilogramos de alimento per cápita que hemos obtenido para 1965 a partir de los cálculos de Carpintero, en cambio, son, junto a sus respectivas categorías, los siguientes.
Categorías |
Coeficientes (m 2 /kg) |
Cantidades (kg/habitante) |
Productos vegetales |
3,07 |
609,03 |
Trigo |
9,52 |
136,80 |
Arroz |
1,81 |
8,33 |
Judías |
17,18 |
4,32 |
Lentejas |
21,53 |
1,12 |
Garbanzos |
20,13 |
3,70 |
Hortalizas |
0,53 |
201,87 |
Tubérculos |
0,77 |
160,11 |
Cítricos |
0,63 |
34,40 |
Frutales |
1,80 |
56,33 |
Carne de ganado |
16,97 |
22,40 |
Bovino |
23,16 |
7,49 |
Porcino |
19,67 |
11,01 |
Ovino |
1,41 |
3,54 |
Caprino |
6,53 |
0,37 |
Aves |
14,09 |
4,64 |
Conejo |
20,76 |
0,82 |
Pescado |
120,60 |
30,89 |
Los coeficientes para “productos vegetales” y “carne de ganado” se obtienen por ponderaciones de los coeficientes de las categorías que engloban, por lo que de momento podemos prescindir de ellos.
Se puede ver que las categorías de alimentos no corresponden totalmente. No queda más remedio que agregar al nivel máximo consentido por las dos fuentes, pero ¿Qué ponderaciones utilizar para calcular el coeficiente de huella de la nueva categoría? ¿En qué casos supone un problema?
Para empezar, podemos agregar las categorías de pan y pastas de la EPF para obtener el equivalente de “Trigo” y esto no supone problema[39]. Podemos agregar también los datos de lentejas, garbanzos y judías de Carpintero para obtener la categoría “legumbres” de la EPF[40].
Sumando “naranjas” y “limones y otros agrios” obtenemos “cítricos”. Aquí no podemos hacer otra cosa que tomar el coeficiente tal como nos lo presenta Carpintero.
Podemos considerar equivalentes “hortalizas” y “hortalizas y otras verduras”. Sumando “plátanos” y “otras frutas frescas” obtenemos “frutales”. Siendo la patata prácticamente el único tubérculo consumido en la dieta española (especialmente en los años ’60, en que no se habían introducido todavía variedades de otras latitudes) no supone un problema suponer análogas las categorías de “patatas” y “tubérculos”.
El ovino y el caprino pueden agregarse para equipararse a la “carne de lanar”.
No tenemos tampoco datos del consumo de carne de conejo a nivel provincial, si bien la EPF (en el resumen estatal) indique un consumo estatal de 1,31 Kg por persona y año de “Otras carnes”; esto es coherente con los 0,82 Kg que hemos obtenido intrapolando. El problema con este alimento es que es el único de los utilizados por Carpintero que no está agregado en las categorías principales de la EPF. Sólo quedan dos opciones: imputar el mismo consumo para todas las provincias o excluirlo del análisis. Esta última opción es preferible en la medida que una imputación homogénea no alteraría la distribución provincial de la huella. Por esto, excluiremos a la carne de conejo del análisis provincial de la huella ecológica, pero no del nuevo cálculo estatal.
El caso del pescado sería bastante delicado, tanto porque supone con diferencia el mayor componente de la huella ecológica de la alimentación (nótese lo elevado del valor de su coeficiente, y esto a pesar de que Carpintero utiliza la productividad local, esto es la de las capturas españolas y no la productividad estándar de los mares, que arrojaría un coeficiente todavía más elevado) como porque incluye una gran variedad de especies, con unos requerimientos presumiblemente muy diferentes de espacio. Ante la ausencia de más detalles sobre su elaboración, nos limitamos a tomar el valor de los coeficientes procurado por Carpintero.
Sobre los demás alimentos de que disponemos de datos provinciales y que Carpintero no incluye en su análisis (huevos, leche fresca, queso, aceites, azúcar, vinos de pasto) aquí intentaremos reproducir sus huellas ecológicas. Solo los huevos y el azúcar deberán ser excluidos por ausencia de datos.
Sobre la leche, cuando Carpintero realiza estimaciones sobre la huella de los pastos, nos ofrece datos de la huella por habitante del consumo de leche a partir de una simulación de los requerimientos de tierra en caso de una alimentación extensiva (vía pastizales) del ganado que la produce. Tomando estos datos y combinándolos con los datos del Anuario de la Producción Ganadera del MAPA de 1965 sobre la distribución de la producción de leche entre consumo humano y otros usos y, a su vez, entre leche para consumo humano directo y para producción de queso, obtenemos que los metros cuadrados por habitante destinados a la producción lechera directa eran unos 296 y los destinados a la elaboración de quesos eran unos 60.
Por otra parte, disponemos de los consumos per cápita de leche y de queso en medias estatales. Esto nos debería permitir obtener los coeficientes (m2/litro) para imputar a nivel provincial la huella del consumo de leche y queso. En el caso de la leche tenemos que 296 ha/hab dividido 78,7 litros/habitante, lo que deja un coeficiente de 3,76 m2/litro.
Por otra parte, dividiendo los m2 per cápita dedicados a su producción (60, como hemos visto) por el consumo de queso (1,53 Kg/habitante) por obtenemos el coeficiente que utilizaremos para calcular la distribución provincial de la huella ecológica imputable a este alimento. El resultado es de 39,2, uno de los coeficientes más elevados de los que manejamos. ¿A qué se debe esta intensidad espacial de los consumos queseros?
La razón reside en que solo una pequeña proporción de la leche utilizada acaba convirtiéndose en queso, quedando la mayor parte separada del mismo en el suero o perdida a través de procesos de deshidratación.
El siguiente grupo de alimentos que podemos incluir en nuestro cálculo de la huella ecológica es el del aceite y el vino. Ambos no aparecen en el análisis de Carpintero porque, según dice en el apéndice metodológico, no se dispone de series completas de los mismos para todo el periodo por él estudiado. Pero nosotros, al enfocar la cuestión en perspectiva estática, no tenemos que lidiar con este problema y, al contrario, contamos con datos detallados de consumo. En p.369 Carpintero nos ofrece la huella ecológica por habitante de los cultivos del viñedo y el olivar (entre otros) para los años 1961 y 1975, que utilizaremos para interpolar según el método ya habitual y hallar los coeficientes para el aceite y el vino. En el caso del vino, obtenemos un requerimiento de tierra de 506,71 m2 por habitante, y en el del aceite uno de 649,15 m2/habitante. De aquí es fácil pasar a los 10,67 m2/l del vino y los 26,22 m2/l del aceite.
Como se ha dicho, nada podemos decir sobre los huevos y el azúcar, por lo que nos vemos obligados a excluirlos de nuestro análisis.
Ahora estamos en condiciones de comparar los datos estatales obtenidos con los elaborados por Carpintero.
|
m 2 /Kg |
Huella p.c A (m 2 /hab.) |
Huella p.c. B (m 2 /hab.) |
Trigo |
9,52 |
1302,21 |
1323,15 |
Arroz |
1,81 |
15,06 |
17,54 |
Legumbres |
19,15 |
175,09 |
287,25 |
Hortalizas |
0,53 |
106,33 |
28,75 |
Tubérculos |
0,77 |
123,29 |
84,32 |
Cítricos |
0,63 |
21,56 |
13,48 |
Frutales |
1,80 |
101,19 |
63,59 |
Bovino |
23,16 |
173,48 |
167,69 |
Porcino |
19,67 |
216,46 |
39,72 |
Lanar |
1,72 |
6,71 |
8,63 |
Aves |
14,09 |
65,42 |
71,58 |
Conejo |
20,76 |
16,94 |
0 |
Pescado |
120,60 |
3725,31 |
3039,17 |
Leche |
3,76 |
0 |
295,91 |
Queso |
39,2 |
0 |
59,97 |
Aceite |
10,67 |
0 |
264,12 |
Vino |
26,22 |
0 |
1245,33 |
|
|
|
|
Vegetales |
|
1844,76 |
1818,11 |
Carne |
|
479,03 |
287,64 |
Pescado |
|
3725,31 |
3039,17 |
Otros |
|
0 |
1865,34 |
Total sin otros |
|
6049,11 |
5144,93 |
Total |
|
6049,11 |
7010,27 |
La Huella p.c. A indica la huella ecológica por habitante calculada a partir de las cantidades estimadas para 1965 a partir de los datos ofrecidos por Carpintero, y la Huella p.c. B hace lo propio con los datos ofrecidos por la EPF. Si no consideramos los alimentos no incluidos en la estimación de Carpintero obtenemos una huella ecológica de unos 900 m2 por habitante inferior a la que se deduce de los datos utilizados por Carpintero (un 15 inferior). En cambio, al incluir la leche, el queso, el aceite y el vino obtenemos una huella ecológica de unos 1.000 m2 superior.
La huella ecológica de la alimentación española y su distribución territorial
Ahora, finalmente, podemos obtener la huella per cápita de la alimentación española lo más completa posible en 1965 en su dimensión provincial. Para ello, basta con aplicar los coeficientes de requerimientos de espacio por unidad de medida (kg o litros) de los alimentos en combinación con los datos de consumo de alimentos en cantidades. En los mapas abajo reproducidos se reproduce la distribución provincial de la huella ecológica per cápita. Como el pescado oculta otras realidades (dada su magnitud en exigencias territoriales y su relativamente pequeña entidad en peso) se ha reproducido la huella p.c. con y sin el pescado. Con el pescado lo más destacado es como la huella ecológica tiene una correlación débil tanto con las provincias con mayor renta como con las áreas más urbanizadas. Pueden verse los resultados en los gráficos correspondientes. Excluyendo a las provincias de Orense y Pontevedra (que por su elevado consumo de pescado tienen las huellas ecológicas per cápita de la alimentación más elevadas de España) la correlación parece aumentar, aunque sigue sin ser especialmente explicativa dada la gran dispersión de los datos. La relación entre ingresos y huella ecológica per cápita es de hecho incluso más débil que la correlación con la ingesta de nutrientes animales. Al obviar el pescado la relación parece aumentar, pero sigue sin ser clara y ni siquiera se alcanza un R2 de 0,3. Habiendo visto las pautas de la distribución territorial de los diferentes alimentos, a primera vista no se puede decir nada más que la composición de la dieta (y con ella su impacto ecológico) parece obedecer a una combinación de elementos económicos pero también culturales vinculados con el medio, como las dietas intensivas en pescado de las zonas costeras o los grandes centros comerciales, o aquellas vinculadas a la leche y al vino allá donde estas producciones eran ya típicas de la agricultura tradicional. De este modo, toda la franja norte manifiesta las grandes exigencias espaciales que implica una dieta rica en proteínas animales, bien sea carne, pescado, o lácteos. Por otra parte, hemos visto como el mecanismo de los precios relativos explica parcialmente pero no totalmente estos fenómenos y en pleno desarrollismo las provincias económicamente más avanzadas no son las que tienen una dieta con mayor impacto territorial relativo.
 |
| Figura 13. Huella ecológica por habitante e ingresos per cápita. |
 |
| Figura 14. Huella ecológica de la alimentación de las provincias españolas. |
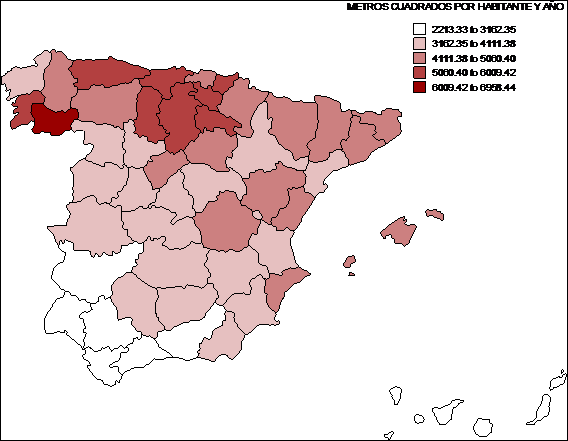 |
Figura 15. Huella ecológica de la alimentación de las provincias españolas (sin incluir la huella ecológica del pescado). |
Notas
[1] Entre éstas últimas se situarían las necesidades de respirar, beber, comer, satisfacer el placer sexual y la necesidad de ser amados, comprendidos y recibir apoyo emocional; incluso estas últimas habrían sido seleccionadas naturalmente y habrían cumplido un papel evolutivo fundamental en la formación del moderno Homo sapiens sapiens, “genéticamente” social. Véase al respecto Harris, M., “Nuestra especie”, 2006.
[2] Al respecto, ver la polémica sobre la (supuesta) necesidad humana, que Harris niega, de maximizar el éxito reproductor, en Harris, 2006, p. 194-200.
[3] Dicho índice, elaborado desde 1990, consiste en una media ponderada de tres indicadores normalizados, respectivamente de PIB per cápita, esperanza de vida y educación (siendo este último, a su vez, un indicador elaborado a partir de la ponderación de las tasas de alfabetización de adultos, a la que se asigna una ponderación de 2/3, y de las tasas de matriculación, a la que se asigna 1/3). A cada uno de los tres indicadores se le asigna un peso de 1/3.
[4] Véase “Informe sobre Desarrollo Humano, 2007”, PNUD, Nota Técnica 1, pg. 357-363 para una descripción de los diferentes indicadores. Véanse asimismo las notas técnicas del “Informe sobre Desarrollo Humano, 1997” para las propiedades matemáticas de los diferentes indicadores y el sentido de su sensibilidad ante cambios en las ponderaciones.
[5] Cowell, F., “Measurement of inequality”, en Atkinson, A. y Bourguignon, F. (eds.) “Handbook of Income Distribution”, 1999.
[6] Donde μ(y) es la renta media e I(y) es un indicador de la desigualdad de la distribución de la renta y donde δW/δμ> 0 y δW/δI<0; es decir, el bienestar social debe aumentar si aumenta la renta media (sin que lo haga la desigualdad) y disminuir si aumenta la desigualdad (sin que lo haga la renta media)
[7] Ver el capítulo 1, “Eguaglianza di che cosa?” de Sen, A. “La diseguaglianza. Un riesame critico”.
[8] Donde los datos del conjunto nacional están derivados de la suma de los datos urbano y suburbano, con el inconveniente que más adelante se describe.
[9] Dichas categorías son: agricultores; obreros agrícolas; patronos y trabajadores independientes; profesiones liberales y asimiladas; directores gerentes de empresa y compañías; empleados, administrativos, oficinistas; empleados, trabajadores manuales; empleados, personal de servicios; miembros de fuerzas armadas; personas económicamente activas no clasificables; población independiente no activa.
[10] Desgraciadamente, el INE dejó de realizar encuestas de este tipo tras la de los primeros años noventa y optó por recabar información sobre presupuestos familiares a través de la Encuesta Continua de Presupuestos Familiares (ECPF), que ofrece la ventaja de una alta frecuencia en la distribución temporal de las muestras recogidas y un coste más reducido pero pierde representatividad al nivel regional, por no hablar del provincial, a causa del tamaño más reducido de la muestra, sólo parcialmente paliado por su ampliación en 1997.
[11] Ver, al respecto, Goerlich y Mas (2001) y Ayala, Jurado y Pedraja (2005).
[12] Por ejemplo, en los trabajos de los Alcaide, que calculan para el conjunto de España índices de desigualdad y distribuciones de ingresos para las diferentes categorías a partir de los datos provinciales agregados sin alguna ponderación.
[13] Correspondiendo éstos a lo que en la clasificación censal serían los estratos rurales y los estratos intermedios, esto es poblaciones con menos de 5.000 habitantes y de entre 5.000 y 10.000, respectivamente
[14] Véase al respecto “Encuesta de Presupuestos Familiares. Desarrollo”, publicación del INE de 1964 con descripción metodológica de la encuesta y su diseño y J. B. Pena Trapero, 1964.
[15] Por ejemplo, Goerlich y Mas (2001) hablan de “factores de elevación” (elevation factors ) al tratar sobre este tipo de problemáticas en su estudio de las EPF de 1973-74, 1980-81 y 1990-91, aunque hemos considerado conveniente utilizar la terminología empleada por Atkinson, a nuestro juicio más gráfica y si se quiere más intuitivamente accesible, de “ponderar por (características de la) población” (population weighting).
[16] Esta última puede hallarse fácilmente a partir de una sencilla ecuación de primer grado; véase, a propósito, Cowell (2000).
[17] Von Fintel (2007), que concluye que realizar estimaciones a partir de las observaciones puntuales no genera resultados significativamente diferentes respecto a estimaciones realizadas tomando el punto medio de los intervalos.
[18] Con límite superior 1 (puesto que toda función acumulativa debe tender asintóticamente a 1, es decir debe llegar un punto en que toda la población haya quedado contada). Para estos cálculos se ha empleado el paquete SPSS.
[19] En nuestro caso, esta tiene la forma f(x)=–a(b^ln(x))ln(x)/((a(b^ln(x))+1)^2)x
[20] La que reza en la portada “Encuesta de presupuestos Familiares. I-Estimación de las características poblacionales; II-Consumo de productos alimenticios. III-Elasticidades demanda renta”.
[21] En el cuadro aquí presentado hemos sumado los hogares de 10 miembros y los de 11 o más; de este modo la información así obtenida puede combinarse, como más adelante se explica, con los datos del censo (que llegan solamente hasta 10 o más) para realizar estimaciones de la renta personal. también nos hemos limitado al segundo decimal de los porcentajes en la presentación, aunque para evitar distorsiones en las categorías con menor peso hemos utilizado como mínimo 8 decimales en los cálculos.
[22] Véase, al respecto, Aldás, Goerlich y Mas (2006) y los datos referidos a dicho trabajo en http://www.ivie.es/banco/desig.php
[23] Véase Cowell (2000), pg. 96-98.
[24] Tal es el caso de Aldás, Goerlich y Mas (2006) y de Ayala, Jurado y Pedraja (2005), para citar estudios sobre la desigualdad con la perspectiva territorial y focalizados en España para periodos posteriores al nuestro.
[25] Para el caso en que tengamos frecuencias y no observaciones, las fórmulas son: Atk(ε)=1-[∑infi(xi/μ)1-ε]1/(1-ε) si ε≠1 y 1-exp[∑in fi ln(xi/μ)ε] para ε=1.
[26] Alcaide, J., 2003, pg. 424-425.
[27] Varela, García y Moreiras Varela, 1971.
[28] En realidad, buena parte de la obra desglosa la aportación en nutrientes de cada uno de los 126 alimentos de la lista amplia de la EPF para las 12 regiones en que están clasificados los datos. Al final de la obra se recogen unas tablas provinciales en que se detallan las agregaciones de nutrientes para cada provincia. Puesto que en los datos de lo Encuesta no figura la información provincial desglosada relativa a los 126 alimentos, cabe suponer que esta estimación a) fue realizada a partir de los microdatos de la encuesta (aunque lo dudamos, porque de ser este el caso, dado el enorme volumen de trabajo que supondría, por lo menos habría sido dicho en algún lugar de la misma obra o, incluso, podría haberse realizado el desglose por alimento detallado a nivel provincial y no regional); b) fue realizada solamente a partir de los datos provinciales, realizando una estimación media de las aportaciones de nutrientes de las diferentes categorías agregadas de alimentos; c) fue realizada proyectando las categorías detalladas a nivel regional sobre los agregados de las mismas a nivel provincial (la opción más probable).
[29] Lo anterior es cierto en general excepto para los índices de Gini y para los índices de Atkinson con parámetro de aversión a la desigualdad ε=2.
[30] Cussó, 2001, pg.152-157.
[31] Incluye tomates, pimientos, coles y repollos, judías verdes, lechugas, alcachofas, acelgas, puerros, cebollas y cebolletas, guisantes verdes, espárragos, zanahorias, espinacas, coliflor y “otras verduras”.
[32] Alubias, garbanzos, lentejas y “otras legumbres secas”.
[33] Manzanas, peras, melocotón, albaricoque, guindas, cerezas, ciruelas, melones, uvas y “otras”.
[34] Sardina, boquerón, jurel, besugo, gallos, pescadilla, merluza, calamares, bacalao, atún y bonito, congrio, rape, mero y raya, palometa, otros pescados frescos, pescadilla, merluza y otros pescados congelados.
[35] Exceptuando, en el primer caso, el área astur-cantábrica (con puntas de consumo de alrededor de los 30 litros anuales) y, en el segundo, la gallega.
[36] Para transformar los quesos hemos utilizado un coeficiente de 1 a 10 para calcular el consumo equivalente de leche y hemos utilizado los coeficientes de la leche (1,806 gramos de calorías diarias por cada litro de consumo anual, 0,405 gramos de proteínas por cada litro de consumo anual y 0,0979 gramos de lípidos por cada litro de consumo anual); hemos utilizado los coeficientes medios del pescado[36] (1,56, 0,2639 y 0,0462 respectivamente); para los huevos (de los que solo disponemos del consumo anual en unidades) hemos supuesto 50 gr por unidad y un coeficiente de pérdida del 11% para deducir el peso de la cáscara
[37] Aunque quizás la mayor correlación entre ingresos y peso de las proteínas animales en la ingesta calórica total pueda llevar a engaño: de hecho las provincias de la mitad occidental del norte (que son también las más pobres del norte) tienen mayores niveles de consumo de proteínas animales pero también mayores niveles totales de ingesta de proteínas, por lo que el peso de las primeras se ve así artificialmente reducido.
[38] Puesto que el porcentaje de menores de 14 años está fuertemente correlacionado con el porcentaje de mayores de 60 años y, para evitar problemas de multicolinealidad, utilizaremos solamente la primera variable, interpretando en sentido contrario el efecto de la variable si el signo del parámetro estimado es negativo.
[39] Especialmente porque el consumo de pastas medio era en esos años de 4,5 Kg anuales per cápita, frente a un consumo de pan de 134,5 Kg que se llevaba, pues, la parte del león en las formas de consumo de los cereales.
ALCAIDE INCHAUSTI, A. y ALCAIDE INCHAUSTI, J. Distribución personal de la renta en España y en los países de la OCDE, Hacienda Pública Española, nº 47, p. 17-57, 1977.
ALCAIDE INCHAUSTI, A. y ALCAIDE INCHAUSTI, J. Distribución personal de la renta española en 1980, Hacienda Pública Española, nº 85, p. 485-509, 1984.
ALCAIDE INCHAUSTI, A. y ALCAIDE INCHAUSTI, J. Metodología para la estimación de la distribución personal de la renta en España en 1970, Hacienda Pública Española, nº 26, p. 55-63, 1974.
ALCAIDE INCHAUSTI, A. Elasticidades de demanda-renta de los consumidores españoles, Estadística Española, nº 39, p. 5-26, abril-junio 1968.
ALCAIDE INCHAUSTI, J. Evolución económica de las regiones y provincias españolas en el siglo XX. Bilbao: Fundación BBVA, 2003.
ALCAIDE INCHAUSTI, J. La distribución de la renta. In GARCÍA DELGADO, España, economía, 1991, p. 639-667.
ALDÁS MANZANO, J., GOERLICH GISBERT, F.J. y MAS IVARS, M. Gasto de las familias en las comunidades autónomas españolas. Pautas de consumo, desigualdad y convergencia, CIEF y Fundación Caixa Galicia, 2006 y los datos al respecto on line en http://www.ivie.es/banco/desig.php.
ATKINSON, A.B., y BOURGUIGNON, F., (eds.). Handbook of Income Distribution. Amsterdam: ed. North-Holland, 1999.
AYALA CAÑÓN, L., JURADO MÁLAGA, A. y PEDRAJA CHAPARRO, F. Desigualdad y bienestar en la distribución intraterritorial de la renta, 1973-2000, Papeles de Trabajo del Instituto de Estudios Fiscales, 2005.
AYUSO, J. Cinco años de migraciones interiores en España, Estadística Española, nº 30, enero-marzo 1966.
CANAVOS, G. Probabilidad y estadística. Aplicaciones y métodos, MacGraw-Hill, 1988.
CARPINTERO, O.El metabolismo de la economía española. Recursos naturales y huella ecológica (1955-2000). Madrid: Fundación César Manrique, 2005.
CHUNG, C. y LÓPEZ, E. A regional analysis of food consumption in Spain, Economic Letters, 26, p. 209-213, 1988.
COWELL, F.A. Measuring Inequality, 3rd edition, LSE Economic Series, Oxford University Press, 2000.
CUSSÓ, X. Alimentació, mortalitat i desenvolupament. Evolució i disparitats regionals a Espanya des de 1860”, Tesis Doctoral inédita, Universitat Autònoma de Barcelona, 2001.
GARCÍA ÁLVAREZ, M. La primera encuesta española sobre cuentas familiares, Estadística Española, nº 1, octubre-diciembre, p. 53-59, 1958.
GARCÍA DELGADO, J.L. España, economía. Madrid: Espasa Calpe, 1991.
GOERLICH, F. J. y MAS, M. Inequality in Spain 1973-91: contribution to a regional database, Review of Income and Wealth, series 47, number 3, September 2001.
HARRIS, M. Nuestra especie. Madrid: Alianza editorial, 2006, Séptima reimpresión.
I.N.E. Encuesta de Presupuestos Familiares (marzo 1964-marzo 1965). Resultados provisionales, nacionales y provinciales. Madrid: 1965.
I.N.E. Encuesta de Presupuestos Familiares (marzo 1964-marzo 1965). I. Estimación de las características poblacionales. II. Consumo de productos alimenticios. III. Elasticidades de demanda-renta”. Madrid: 1969.
I.N.E. Estadísticas de la población de España deducidas del padrón municipal de habitantes del año 1965, Madrid: 1969.
I.N.E. Censo de la población de España de 1970. Madrid: 1972.
MINISTERIO DE DEFENSA. Manual de Alimentación de las Fuerzas Armadas. Volumen II, Tablas de composición de los alimentos. Madrid: Ministerio de Defensa, 1983.
NICOLAU NOS, R. y PUJOL ANDREU, J. Nivells de vida: antics i nous problemes, Document de Treball 1-2003, Unitat d’Història Econòmica, UAB, descargable en http://www.h-economica.uab.es/cat/documents/llistat.htm.
NICOLAU NOS, R. y PUJOL ANDREU, J. Alimentació i nivells de vida: algunes reflexions sobre la transició nutricional a l’Europa Occidental, Document de Treball 2-2007, Unitat d’Història Econòmica, UAB, http://www.h-economica.uab.es/cat/documents/llistat.htm.
PENA TRAPERO, J.B. Encuesta de presupuestos familiares, Estadística Española, nº 24, julio-septiembre 1964.
PENA TRAPERO, J.B. Modelo econométrico para el estudio de la distribución personal de la renta en España, Estadística Española, nº 27, abril-junio 1965.
PNUD. Informe sobre Desarrollo Humano 1997. descargable en http://hdr.undp.org/en/reports/global.
PNUD. Informe sobre Desarrollo Humano 2007-2008. descargable en http://hdr.undp.org/en/reports/global.
RODRÍGUEZ ARTALEJO, F., BANEGAS, J.R., GRACIANI, M.A., HERNÁNDEZ VECINO, R. y REY CALERO, J. El consumo de alimentos y nutrientes en España en el período 1940-1988. Análisis de su consistencia con la dieta mediterránea, Medicina Clínica, vol. 106, nº 5, 1996.
SEN, A. La diseguaglianza. Un riesame critico. ed. Il Mulino, 2000.
VARELA MOSQUERA, G., GARCÍA RODRÍGUEZ, D. Y MOREIRAS-VARELA, O. La nutrición de los españoles. Diagnóstico y recomendaciones. Estudios del Instituto de Desarrollo Económico, Madrid: 1971.
VON FINTEL, D. Dealing with earnings bracket responses in household surveys. How sharp are midpoint imputations?, South African Journal of Economics, vol.75, 2, p. 293-312.
© Copyright Martinelli, 2009.
© Copyright Scripta Nova, 2009.
Ficha bibliográfica:
MARTINELLI LASHERAS, Pablo. Contribución al estudio de las desigualdades en la España de los '60: ingresos y alimnetación. Scripta Nova. Revista Electrónica de Geografía y Ciencias sociales. Barcelona: Universidad de Barcelona, 20 de noviembre de 2010, vol. XIII, nº 305. <http://www.ub.es/geocrit/sn/sn-305.htm>. [ISSN: 1138-9788].