
|
UNIVERSIDAD
DE BARCELONA ISSN: 0210-0754 Depósito Legal: B. 9.348-1976 Año XV. Número: 89 Septiembre de 1990 |
Peter Gould y Joseph Kabel
NOTAS SOBRE LOS AUTORES
Peter Gould es geógrafo y profesor de la Universidad estatal de Pensilvania (Filadelfia). Ha publicado en Geo Critica un ensayo de carácter teórico ("Pensamientos sobre la Geografía", Geocrítica nº 68, marzo de 1987) donde puede encontrarse una nota sobre su biografía intelectual.
En los últimos años ha desarrollado un amplio trabajo en el campo de los problemas ambientales y de la geografía médica y en particular sobre la difusión espacial del SIDA. Además de numerosas publicaciones especializadas, que se citan en la bibliografía del artículo que ahora presentamos, Peter Gould ha abordado la presentación al gran público de temas globales desde una perspectiva geográfica.
Entre sus obras más recientes de este carácter citamos:
- Fire in the rain: The
Democratic Consequences of Chernobyl, Cambridge, The Polity Press, 1990;
Baltimore, Johns Hopkins University Press, 1990
-
The New Plague: Geographic
Consequences of the AIDS Epidemic, en publicación.
Joseph Kabel colabora con Peter Gould en trabajos de cartografía temática aplicada a la epidemiología. Ha realizado, entre otros, los siguientes trabajos:
The Diffusión of AIDS, cinta de vídeo de 20 minutos hecha en colaboración con WPSX TV, University Park, PA 1989 (en colaboractón con P Gould y D. DiBiase).
Le SIDA: la carte animée comme rethorique cartographique appliquée, MappeMonde, 1,1990, págs. 21-26 (en colaboración con P. Gould y D. DiBiase).
La traducción del ingles ha sido realizada por Azucena Gozalo Ausín y Jesús A. González López.
LA EPIDEMIA DE SIDA DESDE UNA PERSPECTIVA GEOGRÁFICA
Peter Gould y Joseph Kabel
En este momento nos encontramos aún al principio de una pandemia global de SIDA, una enfermedad para la que no tenemos ni cura ni vacuna, sino solamente una medicación inadecuada que frena el curso de la enfermedad de modo temporal. Se trata de una enfermedad enormemente difícil de controlar, ya que el virus de inmunodeficiencia humana (VIH) es un “virus lento", cuya tipología sólo se conoce desde 1977, habiéndose identificado el VIH específicamente entre los años 1981 y 1982. El tiempo que media entre la infección y la transformación en SIDA es de diez años, sobreviniendo la muerte en un plazo medio de 27 meses. Hasta marzo de 1990 la Organización Mundial de la Salud (OMS) había informado sobre 237.110 casos de SIDA en todo el mundo, y había calculado en 5-10 millones los casos de infección por VIH(1). No cabe duda de que la cifra mencionada es una estimación drásticamente inferior a la realidad en ciertas partes del mundo, de modo particular en África, donde en algunas regiones tendríamos quizás que multiplicar ese valor por diez. En cuanto a la infección por VIH, hay pocos hechos consistentes en los que basar ningún tipo de estimación global. Son pocos los países (con la excepción al parecer de Cuba) que han llevado a cabo pruebas de VIH a nivel nacional, y además la infección varía de modo drástico de un grupo a otro y de región a región.
Mas que intentar presentar una “distribución geográfica del SIDA" como un estudio global, me gustaría centrarme en dos partes del mundo a escalas bastante diferentes; África, a escala continental, y Estados Unidos a escala nacional y regional. La primera nos permitirá calcular los posibles efectos de la pandemia a largo plazo cuando la mayoría de los sistemas de control no están disponibles o no son prácticos; la segunda nos ofrece una oportunidad de examinar con más detalle sus consecuencias geográficas en una parte del mundo donde los datos, aunque lejos de ser perfectos, son mucho más fiables. Es la disponibilidad de datos espaciotemporales razonablemente fiables, números acumulativos de casos de SIDA con coordenadas x, y (geográficas) y t (temporal) lo que permite al geógrafo modelar la difusión de la epidemia en el tiempo y el espacio, contribuyendo así de modo único a nuestro entendimiento científico, nuestra capacidad de intervenir en la epidemia y nuestra habilidad para planificar soluciones humanas para algunas de sus trágicas consecuencias. El modelado de la expansión geográfica del SIDA requiere enfoques nuevos, rara vez vistos en geografía (y al parecer desconocidos en epidemiología), por lo que ofrecemos aquí una extensa discusión introductoria esencialmente pedagógica, en forma de un apéndice matemático, que incluye un ejemplo elaborado por nosotros de filtración adaptativa espacial ("spatial adaptive fíltering"), el enfoque particular que hemos empleado para "predecir" el mapa siguiente.
I. La epidemia de SIDA en África
Aunque no podemos tener una certeza absoluta, hay bases muy fundadas para situar los orígenes de la epidemia de SIDA en África, donde hace unos cincuenta años habrían aparecido dos virus íntimamente relacionados, el VIH-I (África oriental) y el VIH-II (África occidental). Este cálculo se basa en los análisis de dos grupos de investigación de biología molecular, uno japonés y otro norteamericano, que trabajan de modo independiente en la estructura genética de los virus, empleando índices medios de mutación. Todas las evidencias apuntan a un origen africano. A modo de ejemplo, tenemos un modelo geográfico simple pero eficaz basado en las rutas aéreas que unen las 51 ciudades más importantes del mundo, que se ha usado para simular la expansión global del SIDA(2). El mapa final sólo se parece a nuestras actuales estimaciones de la epidemia cuando situamos el origen de la simulación en Nairobi. Además, los dos casos más tempranos identificados en Europa tienen fuertes “conexiones" africanas. El primero de ellos era un marino mercante noruego (y su mujer e hijo) que murieron a finales de los sesenta. Los médicos de Oslo, incapaces de determinar por qué sus sistemas inmunológicos se vinieron abajo con los síntomas hoy bien conocidos de SIDA, congelaron muestras de sangre y suero sanguíneo. Dos décadas más tarde fueron analizadas, resultando ser seropositivas. Este hombre tenía un largo historial de otras enfermedades de transmisión sexual contraídas en sus viajes por África(3). El otro caso fue una joven cirujana danesa que trabajó en los sesenta en un hospital rural de Zaire. Incapaz de diagnosticar su propia enfermedad, regresó a Copenhague, donde murió. Una revisión posterior de su historial médico detallado reveló la existencia de los síntomas clásicos de SIDA, con la casi absoluta certeza de que la transmisión del VIH-I se produjo por un “pinchazo" quirúrgico(4) En último lugar, la extensión e intensidad de la epidemia en África apuntan a la virtual certeza de sus orígenes africanos.
En África oriental, central y occidental la pandemia está teniendo ya consecuencias catastróficas, y esta trágica estimación se reconfirma con cada nuevo informe al respecto. A principios de 1989, la OMS me pidió que revisara 300 "informes" de seroprevalencia en Uganda, Tanzania, Ruanda y Zaire, en la esperanza de que los métodos de modelado geográfico que estábamos usando en Ohio pudieran ser aplicables a la situación africana. Desgraciadamente, se habían empleado enormes sumas de dinero y escasos recursos médicos en una serie de estudios fraccionados y carentes de coordinación, de los que la mayoría eran totalmente redundantes en un sentido teórico de información (es decir, no proporcionaban ideas nuevas), y ninguno proporcionaba las series espaciotemporales (x, y, t) necesarias como base para nuestros métodos de modelado. Se conocían estimaciones del índice de infección por VIH en la población general de Uganda sólo en dos puntos (x, y) y en dos tiempos (t) diferentes. No se puede decir que consiguiera una gran popularidad entre los de la unidad de SIDA de la OMS cuando les dije que los datos eran inútiles desde el punto de vista analítico. En general, los organismos burocráticos, ya sean locales, nacionales o internacionales, no están acostumbrados a escuchar la pura verdad(5).
En esa época (aproximadamente 1987-88), el 80-90% de las prostitutas y “chicas de alterne" de las principales ciudades eran seropositivas, y las estimaciones para los 18 meses transcurridos son mayores. Más del 30% de los camioneros daban positivo en ese momento,(pero los porcentajes para este grupo humano no dejan de crecer en toda la zona desde Somalia a Zimbabwe. Se sabe desde hace mucho que los camioneros son los mayores portadores (6). En 1988 unos médicos cubanos establecieron que el 33% del ejército de Uganda daba positivo, y los efectos de su indisciplinado comportamiento salvaje, de sus saqueos y violaciones en muchas regiones de Uganda y noroeste de Tanzania bajo el régimen de Idi Amin se están dejando notar hoy en día en proporciones aterradoras de SIDA. Más del 25% de las mujeres que llegan al principal hospital de Kampala para recibir cuidado prenatal están infectadas, y en los dos hospitales de misioneros el porcentaje de VIH de la gente que llegaba para todo tipo de cuidados médicos era del 66% (7). A lo largo de la costa noroeste del Lago Victoria se están evacuando áreas completas para escapar de la epidemia, aunque muchos de los que se trasladan están infectados, con lo que llevan la enfermedad a todas parles. Sólo en la provincia de Kasii, aproximadamente 10.000 niños se han quedado huérfanos a consecuencia de la muerte temprana de su padre, cifras que se han estado doblando en los últimos años. Hoy tenemos ya los primeros informes de que en ciertas regiones del área del Valle del Rift se pueden ver los efectos de la epidemia en fotografías de la tierra hechas por satélite. Algunos pueblos han sido abandonados, y los arbustos vuelven a aparecer allí donde la gente ha muerto o escapado de la región.
La expansión del VIH parece haber sido particularmente rápida donde el sistema de carreteras está más desarrollado. Malawi tendría así en la actualidad los niveles de infección más altos que se conocen, con porcentajes del 17% entre los adultos sexualmente activos de las zonas rurales y del 19% en las ciudades, pero los informes que poseemos se quedan probablemente muy por debajo de la realidad. Hace más de un año, hablé con un "observador con conocimientos médicos" que acababa de regresar de Zimbabwe(8), en una época en que el ministro de sanidad era un oficial del ejército, y el número de casos de SIDA presentado a la OMS había sido disminuido respecto a la realidad. El observador extranjero dijo “Se pueden ver evidencias de SIDA por todas partes". En un país tan al sur como Zimbabwe, los porcentajes de infección entre adultos que habían donado sangre por primera vez eran del 15%, mientras que en Lusaka, la capital de Zambia, los porcentajes entre los adultos analizados en el programa médico eran del 32%. Los porcentajes de Mozambique son difíciles de calcular a causa de la guerra civil, pero un muestreo aleatorio alrededor de Beira dio un 10% de infección, y un 24% entre los refugiados que regresaban a sus lugares de origen.
Un aspecto particularmente preocupante de la epidemia en África es que los mismos hospitales y programas médicos pueden ser importantes focos de infección. Las jeringuillas desechables son casi desconocidas en muchas zonas, y muchos hospitales o no tienen medios para la esterilización de las agujas o no los usan. El resultado es que muchos programas de inmunización infantil con financiación internacional están sumidos en el caos, no sólo porque el uso repetido de las jeringuillas extiende la infección entre los niños (causa también de un importante brote entre 35 niños en un hospital soviético), sino porque las vacunas e inoculaciones atenuadas pueden en realidad causar en un niño pequeño las enfermedades que pretendían evitar, si el sistema de inmunidad es ya inmunodeficiente por VIH. Las transfusiones de sangre son otra importante fuente de transmisión, ya que generalmente no se encuentra sangre almacenada en África, donde la mayoría de las transfusiones se llevan a cabo en condiciones de emergencia con donantes locales o familiares. En estas circunstancias es difícil hacer análisis del VIH, y en un importante hospital de Kinshasa los porcentajes de seropositividad eran de aproximadamente un 5%(9)
En África occidental los niveles de infección de VIII se están acercando rápidamente a los de África central y oriental, principalmente por el VIH-II, pero con una veloz ascensión del VIH-I. No es difícil entender porqué: cualquiera que tenga acceso a la World Airlines Guide (guía mundial de las líneas aéreas) y disponga de media hora puede hacer el plano de las capacidades de las líneas aéreas entre las ciudades africanas más importantes, quizás especialmente las que unen el África francófona. Abiyan, capital de Costa de Marfil, aparece como una gran araña en el medio de la tela, y no sorprende saber que se le ha llamado "la encrucijada sexual" de África. En general, sólo pueden permitirse viajar por avión o los muy ricos, o los altos cargos gubernamentales (y sus a menudo enormes séquitos) que tienen que asistir a congresos y que después tienen fines de semana de "descanso y relax" a cargo de los contribuyentes. El resultado es que un tercio de las muestras de sangre de personas infectadas por el VIH en Costa de Marfil dan positivo tanto a la variedad VIH-I como a la VIH-II. En Abiyán, el 60% de todos los pacientes en el hospital de la universidad eran portadores del VIH y el 10% de los donantes de sangre estaban infectados, así como el 10% de las mujeres bajo atención prenatal y la mitad de las prostitutas. Eso era hace algo más de un año (1989). Muy probablemente se tacharán de "exageradas" las especulaciones sobre los efectos últimos de la pandemia en África, pero debería recordarse que los expertos que lanzaron serios avisos hace cuatro o cinco años parecen haber tenido razón. En los primeros años se obstaculizaron los esfuerzos educativos por falta de recursos y a menudo por una clara hostilidad de los gobiernos, que entendían que se estaba “acusando” a África de la enfermedad. Aunque hoy se están haciendo esfuerzos educativos mucho más serios, siguen siendo insuficientes dada la magnitud de la empresa. Lo típico es que un Landrover llegue a un pueblecito, dos jóvenes burócratas de “la ciudad”, arenguen al pequeño grupo que se forma durante diez minutos, les pasen unos pocos folletos y sigan ruta. El impacto de una “educación" de este tipo es obviamente escaso, y la información sobre los preservativos de látex (la única barrera física efectiva contra a transmisión) resulta en esencia carente de significado. Muchos consideran que el impacto último en la sociedad y gobiernos africanos será verdaderamente catastrófico, y se oye con frecuencia hablar de la progresiva desaparición de la élite modernizada. Esto implica que las proporciones de infección por VIH tienden a ser altas entre los grupos mejor educados y urbanos, lo que quiere decir que nos encontraremos importantes incursiones de la enfermedad entre los profesionales médicos, maestros, ingenieros, administrativos, etc En un hospital de Zaire, la infección por VIH entre médicos y enfermeras era de un 20%, no a causa de tratar a enfermos de SIDA, sino por sus propias relaciones sexuales. No deja de ser angustioso el hecho de que las enfermeras jóvenes en África hayan sido consideradas durante mucho tiempo como de fácil acceso para unas relaciones sexuales esporádicas pero “seguras", ya que se asume que tienen el camino abierto para obtener penicilina y otras drogas antivenéreas. Desgraciadamente, estas drogas no tienen efecto alguno ante el VIH(10).
Ningún gobierno está ni puede estar preparado para enfrentarse a una crisis de estas magnitudes. He revisado varias solicitudes hechas por algunos gobiernos de África oriental y occidental a la OMS, en las que piden ayuda para obtener los más fundamentales instrumentos y recursos para enfrentarse a las fases iniciales de la pandemia. Son documentos que inspiran pena y compasión, que, sin pretenderlo, permiten al lector ocasional entender hasta qué punto son angustiosamente inadecuados los recursos médicos disponibles para afrontar tamaña amenaza y que dejan al lector en un estado de absoluta desesperanza. Algunas de las solicitudes (no olvidemos que se trata de solicitudes de una nación a un organismo internacional daban pistas detalladas punto por punto, que incluían papel y sobres y otro material de oficina como cintas de máquina de escribir y ”tres botes de Tipex" (un líquido de corrección para máquinas de escribir antiguas), cuando lo que se necesitaba era... y aquí es donde uno duda. ¿Qué podría frenar la expansión del VIH en un país africano pobre que quizás ya se encuentre en medio del desorden social, político y económico? ¿Un millón de jeringuillas desechables? ¿Seis millones de preservativos de látex?(11). En el mundo existe ya una escasez de látex en bruto, y ha crecido enormemente la demanda de productos como los preservativos, guantes quirúrgicos, etc.. con la consiguiente subida de los precios.
En muchos países del Primer Mundo los esfuerzos educacionales realizados parecen estar teniendo efecto, particularmente en las comunidades homosexuales que aguantaron lo más recio de la primera ola de la epidemia, y en países como Suecia, Noruega, Finlandia y Holanda, que cuentan con buenos programas de educación sexual en las escuelas. Desde 1985 ha sido técnicamente posible parar la expansión del VIH, y quizás estemos empezando a vislumbrar el impacto de nuestros esfuerzos en países con un avanzado sistema médico y educación eficaz. Estas condiciones no se dan en África, Ni siquiera se dan necesariamente en grado suficiente en algunos países con recursos, pero que no los ponen en práctica con la rapidez que debieran. Un ejemplo de estos últimos, que vamos a ver ahora, es Estados Unidos, un país que parece aprender a golpes.
II. La epidemia de SIDA en Estados Unidos
Estados Unidos está a la cabeza de todos los países del mundo capaces de ofrecer cálculos fiables de la extensión de la epidemia de SIDA, con 126.127 casos; 114.381 masculinos y 11.746 femeninos (marzo 1990). Del subgrupo masculino. el 66% de las infecciones se deben a contactos homosexuales, el 18% al uso de drogas intravenosas (IV) y el 8% a ambas formas de transmisión. En el subgrupo femenino, el 52% de las infecciones se deben al uso de drogas IV y el 31% a contactos heterosexuales, de los cuales el 73% lo eran con un usuario de drogas IV o con un hombre bisexual. Sin que sorprenda demasiado, parece haber una fuerte correspondencia con las infecciones por VIH de hace unos diez años, por lo que nos encontramos hoy con casos de SIDA que proceden de infecciones por VIH transmitidas a comienzos de los años ochenta, siendo algunas de ellas de mediados de esta década, ya que parece ser que los drogadictos se ven afectados algo más rápidamente.
La mayoría de los casos restantes se deben a transfusiones de sangre o a componentes de la sangre usados para tratar la hemofilia. Se necesitan aproximadamente 200 unidades individuales de sangre para hacer una sola inyección de Factor B, y aunque se compruebe cada una de ellas rigurosamente, puede haber aún una alta probabilidad de que aparezca el virus (12). En cuanto a las transfusiones de sangre, a comienzos de los ochenta la industria norteamericana de comercio de sangre (de carácter lucrativo) afirmó que el SIDA (VIH) no podía expandirse a través de los productos sanguíneos, y que en cualquier caso era demasiado caro comprobarlo. Da la casualidad de que yo sé que a las Fuerzas Armadas Americanas les cuesta 4,31 dólares (aproximadamente 400 pesetas) comprobar una muestra de sangre. Hoy hay 4.181 personas en Estados Unidos con SIDA avanzado por causa de productos sanguíneos infectados por el virus.
Si estamos viendo ahora más o menos os electos de la infección por VIH de hace 8 o l0 años, ¿qué podemos esperar a lo largo de la próxima década, hasta el año 2000 y en adelante? Es aquí donde nuestra falta de conocimiento sobre las proporciones de la infección por VIH en la población general, y el correspondiente comportamiento respecto a sexo y droga, dificultan en extremo la predicción con modelos epidemiológicos convencionales, ya se basen en la extrapolación estadística o en la dinámica de la transmisión descrita por conjuntos de ecuaciones diferenciales. Hace dos años (julio 1988), mientras asistía a la "Conferencia de la Casa Blanca" ("White House Conference") sobre el SIDA, se intentó hacer un estudio piloto en el cercano Washington DC, para comprobar los materiales y planteamientos que deberían usarse en un estudio nacional detallado de 20.000 familias. Provocó de inmediato gran antagonismo por parte de los políticos locales(13) y fue discretamente "pospuesto". Nadie ha vuelto a hablar del tema fuera de ciertos círculos epidemiológicos especializados.
En ausencia de un estudio nacional en conformidad con los principios aceptados del diseño experimental, sólo podemos calcular los índices de infección por VIH de modo fraccionado en grupos especiales, algunos de ellos en situaciones muy localizadas. Con respecto al VIH (como algo distinto de su conversión en SIDA) uno se pregunta a veces si Estados Unidos, o de hecho la mayoría de los países europeos, están en una situación mucho mejor que Uganda, aunque el SIDA sea una enfermedad de la que hay que informar por ley y los cálculos de la gente con SIDA sean razonablemente fiables hoy en día, incluso si los números calculados en los primeros años requieren métodos especiales(14).
La muestra mayor del mundo, con la excepción del estudio nacional de Cuba, es el resultado de las pruebas hechas a voluntarios de las fuerzas armadas norteamericanas en los últimos cinco años(15). Todo el que entra en el ejército sufre un riguroso examen médico anterior a su incorporación, y las pruebas de VIH forman ahora parte rutinaria del proceso(16). Hay en la actualidad más de dos millones de personas que han sido examinadas, la mayoría entre los 17 y los 23 años de edad.
Aunque el muestreo es enorme, no se ajusta a requerimientos puramente estadísticos, por lo que los especialistas en estadística convencionales tienden a denigrar el informe militar con el pretexto de que es casi con seguridad altamente autoselectivo. En otras palabras, los homosexuales, drogadictos y hemofílicos tienden a ver a los militares como antagónicos con su condición o comportamiento, por lo que se autoexcluyen del servicio militar voluntario. Por otra parte, podemos darle la vuelta al argumento, y decir que en general este estudio puede muy bien representar a la América joven, heterosexual y mayormente fuera de la drogadicción intravenosa. Si una suposición de este tipo tiene alguna validez, los índices de los condados (algo más de 3.300 condados en 50 estados) en 1988 estarían entre cero y diez por mil, con una media de alrededor de 3/1.000. Este es aproximadamente el mismo índice que dio un estudio nacional a gran escala entre estudiantes universitarios, y mucha gente ve estos porcentajes tan pequeños y "lejanos" que no se muestran impresionados, ni por consiguiente preocupados por las posibles implicaciones que pueden tener para ellos personalmente(17). No obstante, siempre que explico la difusión geográfica del SIDA, señalo a mis estudiantes que en la universidad de Penn State tenemos 37.000 estudiantes, lo que quiere decir que hay aproximadamente 110 infectados por el VIH, casi con seguridad sin tener ni idea de su infección, sexualmente activos y por consiguiente capaces de transmitir la enfermedad a otros(18). En general queda un extraño silencio de perplejidad después de haber dado estas cifras
Lo que nos lleva al importante problema de la educación, y mi empleo de la palabra “lejano" para referirme a cómo ven los jóvenes la epidemia tenía claras intenciones. Para mucha gente la epidemia es algo completamente remoto, “algo que les pasa a otros en otras partes", lo que refleja el “síndrome de inmortalidad” que presentan muchos jóvenes. Y sin embargo es precisamente el grupo de jóvenes de entre 16 y 26 años de la población que hemos tenido estos dos últimos años el que tiene mayor “riesgo" hoy en día, ahora que la enfermedad está saliendo de las comunidades homosexuales y de drogadictos, los grupos que sufrieron la fuerza inicial de la epidemia. No supone un gran consuelo para nosotros el que los principales participantes en el reciente Congreso Internacional del SIDA de San Francisco julio 1989) llegasen finalmente a la misma conclusión.
Pero los que se dedican a la educación sanitaria saben bien que educar puede ser extremadamente difícil. Saber que dar información no es suficiente, que debe haber algún tipo de "indicación para la acción", algo que haga a la persona inmediatamente consciente de la existencia de un peligro para su salud, haciéndolo personal, e induciendo así el grado de auto reflexión que genera un cambio real de comportamiento. En el caso de la comunidad homosexual de San Francisco, esa "indicación para la acción" fue ver cómo la mitad de tus amigos enferman de SIDA y mueren. En 1984, el índice de infección nueva era de un 19%; en 1988 y en 1989 era prácticamente cero, pero nuestra preocupación hoy es llegar a los jóvenes con programas de intervención educativa antes de que se den circunstancias tan trágicas como las mencionadas. Es difícil superar el "síndrome de inmortalidad". A partir de estudios a gran escala hechos en Ohio y Massachusetts sabemos que la mayoría de los jóvenes de instituto creen que "a mi no me puede pasar"(19) y en Pennsilvania el 70% de los adolescentes empezaron a tener relaciones sexuales antes de terminar sus estudios en el instituto (a los 17 ó 18 años), el 50% sin usar ningún tipo de sistema anticonceptivo, ni mucho menos la barrera del preservativo de látex. Un estudio longitudinal de tres años de los estudiantes de Penn State mostró un cambio gradual de su comportamiento protectivo, pero quedaba aún un 50% que no usaba ningún tipo de barrera de látex para relaciones sexuales esporádicas.
Y sin embargo sabemos que en muchas regiones metropolitanas el VIH está ya en la población joven. Estamos acostumbrados a calcular los índices "por mil", pero en Nueva York y Miami el porcentaje para los jóvenes de 15 ó 16 años es un uno por ciento, para los de 24 años un tres por ciento, y para los adolescentes huidos de sus casas un 78 por ciento, fundamentalmente a través de la prostitución. Tanto en la América rural como en la urbana, el "crack" (base de cocaína) y las olas de VIH parecen seguirse en sucesión. Así, en el Bronx (Nueva York), un investigador me dijo: "Nos estamos dejando comer desde dentro por un proceso de descomposición espaciotemporal" indicando que el deterioro socioeconómico iba seguido del abuso de drogas y un alto grado de infección por VIH(20). Más del 20% de las mujeres que habían ido a un hospital del Bronx para recibir atención prenatal estaban infectadas, aproximadamente la misma proporción que en Kampala, Uganda. La atención mayor de los medios de información está centrada ahora en el suroeste de Georgia, donde los incitadores a la droga se están trasladando hacia el norte a lo largo de las autopistas desde Florida, haciendo que se "enganchen al crack adolescentes en institutos rurales, los cuates harán cualquier cosa, incluyendo tener relaciones sexuales con traficantes infectados, para obtener una dosis extra. La ola de VIH sigue de cerca la ola de crack(21).
III. ¿Cuál es la situación geográfica de la epidemia?
Hemos visto que tanto en África como en Estados Unidos la pandemia de SIDA está teniendo ya consecuencias que sólo se pueden calificar de catastróficas Y sin embargo mucha gente sigue considerándola "remota", la intervención educativa temprana no parece muy efectiva y además es prácticamente inexistente la planificación a medio plazo de la asistencia médica especializada a gran escala. La pregunta es ¿porqué? No hay una respuesta única ni sencilla, y un estudio y exposición completos revelarían aspectos tales como el prejuicio político y burocrático, el ansia de poder de ciertos profesionales, la pura ignorancia y muchos otros igualmente lamentables aspectos de ha condición humana(22). No obstante, y sin dejar de reconocer la complejidad de una respuesta válida ala pregunta, estamos convencidos de que la causa más importante es el casi total olvido de las dimensiones geográficas de la epidemia. Lo cual no hace sino plantear otra pregunta, ¿por qué? ¿Por qué cuando la consciencia y el modelado geográficos y el análisis y presentaciones de otras enfermedades(23), nos encontramos un desierto baldío de comprensión a la hora de considerar la epidemia de SIDA en el terreno de la geografía?
Hay muchas respuestas parciales. Parte del problema es la angustiosa falta de educación geográfica en muchos programas escolares, que da como resultado una falta genera de conocimiento? Consciencia y sensibilidad hacia el terreno espacial o geográfico. En Estados Unidos, la mayoría de las personas "ilustradas" son analfabetos en geografía, y rara vez se plantean las dimensiones geográficas de la existencia humana Y si esto es verdad para la mayoría, es aún más angustiosamente evidente en el nivel profesional del epidemiólogo, incluso (¿O especialmente?) aquellos en posesión de grados doctorales obtenidos en instituciones prestigiosas. La mayoría de los epidemiólogos no han oído hablar jamás del "modelado espacial”, y en ningún momento de su vida profesional han tenido contacto con estos modos geográficos fundamentales de pensamiento y análisis. En su mayor parte expresan asombro al saber que fueron los geógrafos los primeros entro todas las ciencias en usar los métodos de simulación de Monte Carlo para estudiar procesos de difusión geográfica en los años cincuenta(24). La reacción inmediata, casi pavloviana, de los epidemiólogos hacia el modelado de la expansión de una enfermedad es buscar en la estantería sus conjuntos favoritos de ecuaciones diferenciales, para después desgranar números desde un punto de vista temporal, sin preguntarse jamás dónde podrían estar las víctimas potenciales de la enfermedad. Un distinguido matemático de la Conferencia de la Casa Blanca pensaba que modelado espacial quería decir correr de un lado a otro de Alabama a Wyoming con una ecuación diferencial bien agarrada en la manita.
Desgraciadamente, en lo que se refiere a la epidemia de SIDA estos planteamientos son casi inútiles, ya que no pueden ser parametrizados a partir de datos reales. Por lo que pude observar en el Congreso de la Casa Blanca, el planteamiento típico es dividir la población en grupos cada vez más específicos (haciendo ecuaciones cada vez mayores para que las resuelva el ordenador... ¡qué entretenido!), asumir después que los índices de transmisión entre grupos y dentro de un grupo se pueden calcular (¡los científicos conductistas se encargarán de ese desagradable trabajo empírico!), y finalmente extraer los coeficientes de transmisión a partir de los conjuntos de ecuaciones en forma de una matriz llamada jacobea, para encontrar un valor característico denominado primer valor propio (“first eigenvalue”)(25). Si resulta ser mayor que 1.0, sabemos que la epidemia se incrementará; si es menor de 1.0 la epidemia se extinguirá ¿O es que ya sabíamos esto desde antes? Es fácil imaginar lo que tendría que decir sobre tan profunda conclusión un médico que haya estado al cargo del cuidado de enfermos de SIDA en un hospital de San Francisco desde el principio de la epidemia! Los epidemiólogos tradicionales no parecen hacer mucho más que jugar con sus suposiciones, descubriendo, por ejemplo, que si aumentan los índices de transmisión, la epidemia irá más rápida como tiene que ser, lógicamente, a partir de los conjuntos, emparejados mecánicamente, de ecuaciones decimonónicas. No es fácil ver en qué manera se ha salvado una sola vida humana con estos planteamientos puramente temporales, o cómo se ha frenado una transmisión del virus.
Pero aparte del conservadurismo disciplinario tradicional, la visión limitada de los intelectuales y una general falta de curiosidad y conocimiento de otros posibles planteamientos, hay otro asunto que ha obstaculizado grandemente nuestra comprensión de la epidemia del SIDA en el campo de la geografía. Es el tema de "confidencialidad", la creencia de que desde una ética impecable el historial médico de un paciente sólo puede estar disponible para el personal médico con la cualificación adecuada que esté tratando al paciente en cuestión. Existe el temor, que puede ser real y legítimo, de que tan pronto como se dé algún tipo de coordenadas geográficas (x, y; latitud, longitud; dirección; distrito censal, etc.), se podrá identificar a un paciente de SIDA. Se teme una identificación de este tipo por razones de prejuicio contra los homosexuales y drogadictos, un miedo irracional a la transmisión fortuita y la naturaleza sexual de muchas transmisiones, más que por una fuerte creencia en el derecho a la intimidad del individuo. El resultado ha sido la emergencia de una controversia de carácter altamente emocional de la que ha desaparecido casi totalmente la voz de la razón. Hay una tradición fuerte, y éticamente impecable, entre los que pertenecen a la profesión médica de mantener la confidencialidad del paciente, a la que se han sumado muchas voces de las comunidades homosexuales, muchas de las cuales se han convertido en grupos políticamente organizados y poderosos en Estados Unidos. Se ha hecho muy difícil razonar con estos grupos ya que enseguida se le considera a uno "insensible", o se le acusa de rechazar a los homosexuales. Antes de continuar, quiero que quede claro que estoy totalmente de acuerdo con la protección de la intimidad del paciente, pero este asunto se ha llevado absurda y exageradamente lejos, tanto que se ven seriamente amenazadas nuestra comprensión de la epidemia, y nuestra capacidad para desarrollar una intervención educativa y para planificar de una manera humana. Lo que está en juego es un tema totalmente geográfico! que queda justamente en el terreno espacial en el que la mayoría de la gente tiene poca práctica en pensar.
Vamos a ver lo que esto conlleva.
Las dimensiones geográficas de la confidencialidad
En Estados Unidos los Centros para el Control de la Enfermedad (Centers for Disease Control, CDC) de Atlanta publican el número de casos de SIDA sólo a nivel estatal, arguyendo que los estados les obligan a hacerlo así en un sistema de gobierno federal A su vez algunas autoridades medicas estatales dicen que no pueden hacer públicos los datos de condado, código postal o zonas de censo por una norma de los CDC Es un antiguo mecanismo burocrático, probablemente de los tiempos de Babilonia, que se conoce hoy como “Catch22". En Estados Unidos, el Estado es un nivel de agregación geográfica analíticamente inútil. Es además ridículo desde el punto de vista científico, ya que Rhode Island (el más pequeño) cabe 250 veces en Texas. No obstante, la mitad de los Estados, generalmente aquellos donde la epidemia es particularmente seria publican los casos de SIDA a nivel de condado, y unos pocos a nivel de distrito postal. Hoy en día muchos grupos estatales de seguimiento del SIDA ponen incluso mapas de su estado con el número de víctimas de SIDA en cada condado en las tapas de sus informes mensuales o trimestrales de carácter completamente público(26). Nadie que mire esos mapas podría identificar a una sola persona. Y sin embargo la mitad de los estados todavía se niegan a sacar a la luz ni siquiera datos a nivel de los condados. Incluso en Pennsilvania, para un estudio de la universidad de Penn State, hizo falta La intervención de la Cámara de Representantes para convencer al Consejero de Sanidad de que diera salida a ciertos datos a nivel de condado de la unidad especial de SIDA.
Pero el asunto se vuelve aún más absurdo y dañino para la ciencia. En Los Ángeles tenemos grandes mapas (de 75 x 100 centímetros) que muestran los índices de SIDA por zonas censales(27), algunas de no más de tres o cuatro manzanas, y consiguientemente cinco o seis órdenes de magnitud espacial más pequeñas que el nivel estatal de California, la escala geográfica por debajo de la cual los CDC son reacios a hacer públicos los resultados. En otras palabras, los CDC sólo publican datos a nivel estatal, por ejemplo, para el estado de California, mientras que la unidad de vigilancia del SIDA de Los Ángeles publica información por zonas censales. Nadie que mire los sombreados en rojo, amarillo y verde podría, en manera alguna, identificar a nadie. Se ha representado también la epidemia en secuencias de mapas en el tiempo, que muestran la expansión geográfica diferencial en las poblaciones blancas, hispánicas y negras, usando puntos para cada caso que aparece aleatoriamente dentro de un distrito censal(28). Todos ellos los completaron, en cooperación con la unidad de seguimiento del SIDA en Los Ángeles, los estudiantes de primeros cursos de una universidad local con vistas a un proyecto cartográfico con intenciones sociales. No se ha dañado en ninguna ocasión la confidencialidad de ningún paciente. Un estudio reciente sobre la posibilidad de identificación geográfica, hecho a partir de datos microcensales en Italia, llegaba a la conclusión de que la probabilidad del descubrimiento de un individuo a partir de la clasificación cruzada era aproximadamente 10-11(29). Me baso en esto para afirmar que se ha exagerado en exceso el asunto de la "confidencialidad geográfica", tanto que se ha entorpecido grandemente nuestra capacidad de modelar la epidemia en el tiempo y el espacio. Para modelar, para predecir el siguiente mapa o mapas necesitamos series acumuladas espaciotemporales (x y, t) de pacientes de SIDA a una escala o nivel de agregación geográficos razonables. Sólo entonces podremos predecir las distribuciones futuras, y consiguientemente usarlas para fines humanos.
El SIDA en Pensilvania
Vamos a seguir el desarrollo del SIDA en el estado de Pensilvania (figura 3), un estado de un tamaño una o dos veces superior a Portugal, dominado por las dos concentraciones urbanas de Filadelfia en el sureste y Pittsburg en el oeste. Obsérvese que la secuencia de mapas no presenta las clásicas letras ni otras marcas cartográficas, ya que cada imagen ha sido tomada de una secuencia animada de mapas simulada en el ordenador(30) utilizada después en una presentación televisiva con fines educativos.
La animación cartográfica plantea toda una nueva serie de temas en comparación con los mapas impresos tradicionales, ya que existe la posibilidad del añadido de voz, la señalización con la mano, etc.(31) Existen muy pocos mapas que muestren los totales geográficos de la epidemia de SIDA en ninguna parte del mundo, y creemos que el primer ejemplo de este tipo fue la publicación de una secuencia temprana en Ohio en 1988 (¡a siete años del comienzo de la epidemia!)(32). No es que no se hubieran podido elaborar secuencias similares para España, Francia, ítala, etc., simplemente es que a nadie "se le ocurrió".
La secuencia de la difusión espacial ha sido representada como una "superficie" de SIDA contorneada, basada en los 67 centroides de condado. En esencia, se nos exige, por los requerimientos de la confidencialidad, mirar al desarrollo del SIDA a través de las "ventanas” espaciotemporales de los condados considerados como las unidades de agregación geográfica. Esta secuencia viene representada con un espectro, o "paleta” de color, particular que va del amarillo claro (valores bajos) a los rojos intensos (los valores más altos), pero aún queda mucho por experimentar hasta encontrar las secuencias de color más efectivas para la presentación animada. Es importante señalar que el intervalo entre los colores y los contornos es geométrico, cada cambio de color representa un incremento triple en los casos acumulados do SIDA.
Como muchas otra distribuciones humanas en el espacio geográfico, el SIDA produce fuertes puntos máximos exponenciales que son difíciles de captar de modo efectivo con el más común intervalo aritmético.
El primer caso de SIDA del que se tienen informes en Pensilvania se dio en 1984 en Pittsburg, en la parte occidental del estado, seguido de cinco casos más en Filadelfia y alrededores. Estos pocos casos durante los primeros tiempos de la epidemia plantean algunos ternas de importancia. Trataremos la secuencia resultante como si el SIDA se expandiera de manera totalmente clásica; es decir, con una difusión jerárquica, donde un proceso aparece fuertemente controlado por las relaciones entre las poblaciones y ciudades que configuran la jerarquía de lugar urbano o central, y una difusión por contagio espacial, donde vemos la difusión en el mapa, como una mancha de vino que se extiende sobre un mantel (33). Donde observamos un “salto" en el mapa, digamos por ejemplo de Pittsburg a Filadelfia, no sabemos si una persona infectada por el VIH transmitió en realidad el virus de esa manera, ya que nuestra visión está "filtrada" por la agregación de todos los informes individuales, y por tanto confidenciales, a nivel de condado. Sabemos que algunos de los más antiguos casos de que se tiene información en Pensilvania, Ohio y otros estados fueron el resultado de gente a la que se había diagnosticado la enfermedad en otra parte y que regresaban a morir a casa. Incluso hoy en día, la epidemia afecta principalmente al grupo de los de 20 a35 años de edad, probablemente el grupo más móvil geográficamente que haya conocido el mundo. Como resultado, el SIDA está "en todas partes" un 98% o más de los 3.300 condados dan hoy informes de infección por VIH, algo que desconoce la mayoría de la gente. Para muchos, la epidemia resulta algo literalmente "remoto" y "lejano", cuando está, de hecho, totalmente a su alrededor.
Para 1982 los puntos máximos de Pittsburg y Filadelfia ya han comenzado a elevarse, y podemos empezar a ver un efecto de "canal" con dos alineaciones al oeste y al norte de Filadelfia. Estas coinciden con la autopista más importante de Pensilvania (PennsyivaniaTurnpike) que va a Pittsburg y su extensión norte que parte de Filadelfia. El examen de muchas secuencias de mapas (Ohio, toda la costa oeste, etc.) permite ver claramente que la estructura del espacio geográfico humano guía fuertemente la difusión geográfica de la epidemia. Lo que no debería sorprender a los geógrafos: el VIH se transmite de persona a persona sin necesidad de un intermediario, por lo que podríamos esperar que el virus siga las grandes alineaciones de la interacción espacial humana, un área de la geografía humana donde "el pensamiento basado en el modelo de gravedad" ("gravity model thinking") juega un papel de natural importancia (ver el apéndice matemático).
En 1983 podemos ver que tanto la difusión por contagio espacial como la jerárquica tienen que ver en la expansión del SIDA: se da una dispersión hacia afuera de los epicentros regionales, y un salto hacia adelante de estas ondas hacia poblaciones y ciudades más pequeñas de Pensilvania. Para 1984, un cierto número de las que quedan fuera de los epicentros se han fundido, y si pudiéramos presentar una visión mucho más detallada de la geografía de Pensilvania veríamos también el comienzo de una tercera gran alineación. En 1985 podemos ver cómo las curvas isosidas ("iso AIDS contour lines") del área occidental se van acercando a la aún discontinua área oriental, dominada por el punto máximo de Filadelfia. Esta alineación es la carretera 220, una antigua ruta que une una serie de ciudades más pequeñas (Johnstown, Altoona, State College, Williamsport) a lo largo del históricamente famoso Frente de Alleghny, una alineación que se muestra aún más prominentemente en los mapas correspondientes a 1986 y 1987.
De hecho, el desarrollo secuencial de estos mapas de difusión, que termina en 1988 con 2.401 casos conocidos, es un proceso similar a mirar una placa fotográfica que se está revelando en la cámara oscura. Cada mapa parece salir de modo lógico del anterior, y es un ejercicio interesante dar a la gente un mapa en blanco del contorno de Pensilvania y dejar que predigan qué aspecto tendrá en 1988. La mayoría de la gente, incluso aquellos que carecen de preparación geográfica profesional, pueden dar estimaciones extremadamente buenas basándose exclusivamente en su intuición, previsiones que muestran un alto grado de correlación con el mapa real de 1988. Lo que nos lleva de nuevo a la cuestión de la predicción del siguiente mapa o mapas en la secuencia, y a cómo se pueden usar estas previsiones geográficas. Para combatir la epidemia de SIDA se requieren muchas perspectivas, muchas ayudas, muchas áreas de competencia y conocimiento, de la biología molecular, la virología, la medicina, la epidemiología, la educación, de los asistentes sociales... y de los geógrafos. Veamos cuál podría ser la contribución geográfica.
La predicción del mapa siguiente
Al observar la secuencia de mapas coloreados, y al tener enseguida la fuerte intuición de que uno mismo podría predecir sin mucho problema el mapa siguiente, está claro que hay un alto grado de orden espaciotemporal en la secuencia resultante. Al volver a las matemáticas y los ordenadores lo único que pretendemos es hacer computable y bien definido lo que ya sentimos como cierto a nivel puramente intuitivo. El problema fundamental es uno que es muy general en la ciencia, ya que muchos científicos trabajan con el espacio (x, y, y a veces z) y el tiempo (t). Y sin embargo sigue siendo cierto que a ninguno de nosotros, geógrafos, físicos, químicos, biólogos... se nos da demasiado bien buscar la estructura en esas series espaciotemporales (x, y, t). Se puede pensar en ellas o bien formando un cubo de datos, en nuestro caso cada uno de los valores numéricos de los casos acumulados de SIDA con un marcador posicional (x, y) y uno temporal (t), o bien poniendo los mapas de nuestra secuencia de difusión uno encima de otro. Lo que queremos explorar, describir y matematizar es la estructura espaciotemporal de esos cubos o montones, para poder comparar los mapas siguientes en el horizonte temporal.
Hemos utilizado tres planteamientos, dos de los cuales presentamos con más detalle en el apéndice matemático, el método de expansión y la filtración adaptativa espacial(34). No es necesario entrar en grandes detalles, pero la idea básica, como muchas de las ideas científicas con trascendencia, es relativamente simple. Los dos planteamientos estudian el modo en que una ecuación que relaciona una variable (digamos el número de gente con SIDA) con otras que la predicen (como los valores simples de población, los índices socioeconómicos, etc) puede cambiar o “vagar” en el espacio (x, y) y en el tiempo (t). Se puede calibrar una ecuación de expansión, o un filtro de adaptación espacial (generalmente una simple función lineal o cuadrática), a partir de conjuntos reales de datos que configuran una serie espaciotemporal, con lo que se pueden usar para computar los valores siguientes en un sitio en particular (x, y) cuando el tiempo haya avanzado a 1991,1992, y así sucesivamente.
Pero, ¿cuáles son las razones para hacer esto? ¿Mera curiosidad académica? En absoluto. Podemos dirigir estos mapas previstos hacia dos áreas de crucial importancia, la intervención educativa y la planificación médica, contribuyendo así directamente a salvar vidas ya atender a los afectados. Hemos descubierto que cuando las secuencias de mapas, incluyendo los mapas previstos, se preparan para la animación televisiva parecen conformar algunas de aquellas “indicaciones a la acción" que buscan los que se ocupan de la educación sanitaria. España, por ejemplo! presentaba 5.295 casos y el segundo índice más alto de Europa en marzo de 1990, comparable a los porcentajes de Burkina Faso y Dominica. No tenemos conocimiento personal de las proporciones e intensidad de la campaña educativa contra el SIDA en España, pero la educación es hoy por hoy nuestra única esperanza. ¿No les sería posible a los geógrafos españoles trabajar con sus colegas de la medicina, mostrarles las posibilidades de la cartografía animada y, en colaboración con la televisión nacional, producir una secuencia animada similar para España que se pudiera usar para la retransmisión pública, la educación en las escuelas y universidades; etc.?
En segundo lugar; es ya angustiosamente obvio en las regiones metropolitanas grandes de Estados Unidos que los sistemas de asistencia sanitaria están siendo utilizados más allá de sus límites. Tendremos que planificar nuevas formas de asistencia sanitaria (hospitales, hospicios, clínicas para pacientes no internados, etc.) que deberán ser accesibles para los afectados de SIDA, no basándose en la tesis positivista capitalista de la eficiencia medida exclusivamente en términos económicos, sino basándose en sentimientos humanos, de modo que las familias de los pacientes con SIDA puedan visitar a sus hijos, hijas, padres, madres, hermanas, hermanos y amigos. Dónde colocar tales instalaciones para complementar las sobrecargadas ya existentes se convierte en una importante cuestión en la panificación de la salud. Esta ha sido el área clásica de investigación geográfica en los ultimos 25 años, resuelta esencialmente con miras totalmente prácticas Tenemos hoy docenas de algoritmos computerizados para resolver todo tipo de variaciones del tema básico localización-asignación. He aquí otro terreno donde puede contribuir la perspectiva del geógrafo. Vencer el SIDA va a suponer esfuerzos largos y continuos en muchos frentes distintos. Pero los geógrafos tienen aquí una oportunidad literalmente vital de contribuir con sus conocimientos tanto a la ciencia como a la humanidad.
APÉNDICE METODOLÓGICO: LAS SERIES ESPACIO - TEMPORALES Y LA PREDICCIÓN DEL MAPA SIGUIENTE.
Como apuntamos en el texto principal, nos encontramos al comienzo de una pandemia global de una enfermedad con una tasa de mortalidad cercana al ciento por ciento, sin cura ni vacuna a la vista. Como geógrafos, tenemos la responsabilidad de usar nuestra perspectiva espacial :
1) para esclarecer la pandemia del VIH (y su conversión en SIDA) en las dimensiones espaciales de la existencia humana, y así superar la perspectiva temporal, tradicional y normalmente limitada, del epidemiólogo;
2) para facilitar a la televisión material cartográfico animado que sea visualmente efectivo, de manera que proporcione “indicaciones para la acción" a las campañas de intervención educativa y
3) para predecir futuras distribuciones geográficas de víctimas de SIDA que ayuden en la planificación de la ampliación de instalaciones sanitarias que desahoguen la ya saturada red existente (hospitales, hospicios, etc.). Todos estos cometidos, comprensión, educación y planificación requieren nuestra predicción del mapa o mapas siguientes.
La predicción de dicho mapa es un problema geográfico muy general, que requiere que computemos a partir de la información contenida en una serie espaciotemporal (x, y, t) las futuras distribuciones espaciales más probables. como geógrafos, esto lo hacemos de modo intuitivo continuamente. con una simple ojeada a la secuencia de mapas que muestran la difusión del SIDA en Ohio (figura 1) o en Pensilvania (figura 4) está claro que usted mismo podría predecir y dibujar la próxima “superficie del SIDA" en un mapa en blanco, probablemente con un alto rado de precisión.
En cierto sentido, el mapa se “revela" como una placa fotográfica en la cámara oscura: la imagen futura está de algún modo latente en la historia espacio-temporal del proceso de difusión en desarrollo. Las aproximaciones matemáticas que aquí se presentan sólo convierten en operacional y bien definida la intuición sobre la dinámica geográfica que todos compartimos en alguna medida.
Las operaciones matemáticas no deberían incomodarnos Es esencialmente la aritmética que aprenden los niños, las operaciones binarias de adición (+> sustracción (-), multiplicación (x) y división (/). Quizás sea un alivio el que hoy en día todas las matemáticas computables sean aritméticamente triviales. Da igual la forma simbólica o algebraica que presenten, con todos sus subíndices y superíndices, si las operaciones son realmente computables (es decir, son prácticas y útiles, no simplemente un ejemplo de ostentación histriónica), deben reducirse a la aritmética de un niño de diez años para que el “idiota de alta velocidad", el ordenador digital, pueda realizar su trabajo.
Parámetros de variación espacial
Aunque este apéndice metodológico se va a centrar en el muy poderoso enfoque de la filtración adaptativa espacial (“spatial adaptive filtering", SAF), señalando las fuertes analogías existentes con las redes neuronales, con la visión artificial (robótica) y con la identificación de configuraciones, es importante situar la SAF en un contexto geográfico y conceptual más amplio.
A riesgo de resultar repetitivo, empecemos con una manera clásica de plantear casi cualquier problema de di fusión geográfica, refiriéndonos nuevamente al ejemplo concreto del SIDA en Ohio (figura 1).
Figura 1

En la terminología clásica, es obvio que son dos los tipos de difusión jerárquica, ya que al VIH (y su subsecuente diagnosis de SIDA) asciende a través de la jerarquía urbana, fuertemente controlada por las relaciones entre grandes centros urbanos definidos por la interacción espacial humana. En segundo lugar, hay también una fuerte evidencia de difusión por contagio espacial, ya que la enfermedad se extiende como una mancha de vino sobre un mantel desde los epicentros regionales más importantes, rellenando el mapa a medida que se filtra en las áreas rurales.
Podemos ser más explícitos en nuestro planteamiento. Después de todo, el VIH se transmite de persona a persona sin necesidad de un intermediario vivo, de moto que las grandes alineaciones de interacción espacial humana deberían reflejar flujos importantes de transmisión. Hemos llegado, claramente, a una forma del modelo de gravedad, en el que la interacción es una función directa del número de personas, y una función inversa de la distancia, coste o tiempo que les separa. Usemos por tanto una idea tan aparentemente simple como la de la aplicación (una transformación) en su sentido matemático literal, es decir como una regla que lleva un conjunto de elementos (el conjunto inicial) en una aplicación biyectiva (una transformación) a otro conjunto (conjunto final). Esto nos permite literalmente transformar el mapa convencional de espacio geográfico en un espacio multidimensional de interacción humana (o SIDA) (figura 2). Un matemático lo expresaría así:
Figura 2
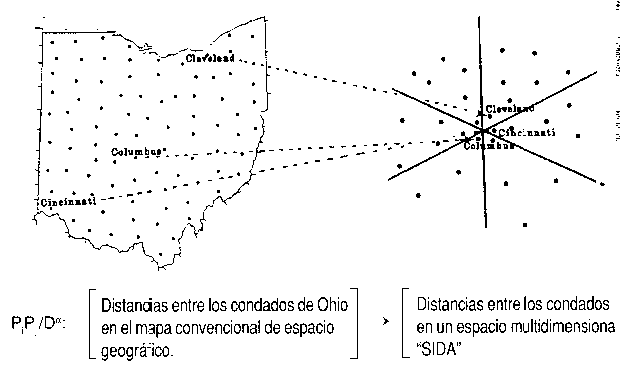
Si hacemos las distancias en el espacio SIDA inversamente proporcionales a la transformación del modelo de gravedad, las grandes ciudades, con sus grandes poblaciones. aparecerán más juntas en el centro del espacio SIDA, mientras que los condados rurales, menos densamente poblados. aparecerán en la periferia de la nube multidimensional de puntos (aunque estarán en el cuadrante cercano a su epicentro regional en el espacio geográfico tradicional). Las relaciones centro-periferia son importantes en todas las escalas geográficas, y es fácil visualizar lo que una transformación de este tipo haría al mapa convencional de España.
Podemos ahora hinchar una burbuja multidimensional centrada en Cleveland (el primer Centro que diagnosticó el SIDA), y dejarle “capturar” puntos de condados al expandirse, limitando así el proceso a una difusión por contagio espacial en el espacio SIDA transformado de modo apropiado. A medida que se expande la burbuja, y "transmite" el SIDA a otros condados, estos empiezan a su vez sus propias burbujas de expansión... y así sucesivamente. Al definir un valor umbral de SIDA >3, esperábamos inicialmente reproducir el orden de la infección, y de hecho tuvimos un éxito moderado (=0,64). El efecto de a, el exponente o fracción de distancia en el denominador de la transformación del modelo gravitatorio, es claramente crucial. De hecho, cuando es alto (a± 1,00), y el efecto de la distancia fuerte (el espacio es viscoso o "pegajoso", y la distancia retarda la expansión del SIDA), la epidemia está controlada por fuertes relaciones reflexivas, y le resulta difícil salir de la esquina nororiental del estado que rodea e epicentro inicial de Clevand (figura 2).
Y a la inversa, cuando es bajo (0,5), y transformamos el orden simulado de la dirección ahora en el mapa convencional, la epidemia salta de Cleveland a Columbus y de ahí a Cincinnati etc., y se extiende a los condados cercanos, reproduciendo con bastante fidelidad el proceso real.
Podemos buscar variaciones combinatorias a partir de aquí, ponderando las “distancias” con el tiempo, coste o condiciones de la ruta (medidas bajas para las carreteras de cuatro carriles y altas para caminos de grava. etc.). pero refinamientos de este tipo no deberían alejar nuestro pensamiento del concepto básico de transformar el mapa convencional en otros espacios más apropiados. La idea fundamental de que ciudades alejadas en el espacio geográfico tradicional aparecen muy juntas en un espacio apropiado de “interacción" aparecerá de nuevo cuando lleguemos a la filtración adaptativa espacial.
El segundo enfoque metodológico también ilustra conceptos geográficos generales y de gran importancia. Estos plantean la cuestión de la manera en que una relación particular puede con el tiempo variar en el espacio geográfico poniendo así tiempo y espacio explícitamente juntos, lo que permite a los geógrafos una aproximación a las series espacio temporales con los instrumentos analíticos apropiados. Entendemos por series espacio-temporales simplemente los valores de datos (como por ejemplo el número de víctimas de SIDA) que aparecen ligados a las coordenadas x, y (geográficas) y t (temporal) Podemos visualizar una serie de este tipo como un cubo de datos en x, y y t, o como un montón de mapas (como los que aparecen en la figura 3) apilados uno encima de otro.
Figura 3
Si bien podríamos estudiar este problema como una simple superficie de tendencias, haciendo del tiempo de llegada del SIDA (T) una función polinómica 1ineal de segundo grado o más, de las coordenadas geográficas (X e Y), este acercamiento se suele frustrar por los altos picos exponenciales en la superficie, puntos muy marcados de población urbana de víctimas de SIDA que no se acomodan muy bien a simples tendencias regionales o geográficas. Un matemático diría que estas superficies puntiagudas muestran “mal comportamiento", y nosotros estaríamos de acuerdo! En lugar de eso, empleamos el método de expansión de la manera siguiente. Pnmero hacemos del SIDA una función cúbica del tiempo:
SIDA= a0 + a1t + a2t2 + a3t3
No se trata de una elección caprichosa: Hay evidencia de que la epidemia crece como una función cúbica, y queremos además que quepa la posibilidad de una ralentización del SIDA, por lo que necesitamos un polinomio simple que se pueda “curvar dos veces", remedando así la curva logística o en forma de “s" de la teoría de difusión tradicional.
La cuestión es ahora si una relación de este tipo se mantiene en el espacio geográfico, y cómo lo hace. ¿Es constante? ¿O acaso cambia o se mueve? esta relación particular en el espacio geográfico, modificándose quizás con alguna otra variable apropiada cuya locación geográfica podemos especificar con facilidad. Técnicamente esto es como decir que los parámetros de nuestra ecuación cúbica en el tiempo a0, a1, a2, a3 pueden cambiar de modo regular con otra variable en el espacio geográfico Dado que el SIDA es una enfermedad humana transmitida de persona a persona, parece razonable observar si la densidad de población podría afectar a los parámetros temporales (¿a mayor densidad mayor probabilidad de interacción y transmisión'?). Hagamos pues explícitamente de estos parámetros funciones de segundo grado de la densidad de población, con lo que nos queda.
a0 = b00
+b01D+b02D2
a1 = b10
+b11D+b12D2
a2 =b20
+b21D+b22D2
a3 =b30
+b31D+b32D2
Ahora todo lo que tenemos que hacer es sustituir estos valores en nuestra ecuación temporal, lo que nos dará una voluminosa pero muy precisa expresión terminal tanto en el tiempo como en el espacio o al menos en una variable geográfica cuya situación espacial podemos especificar con facilidad Tenemos por tanto:
SIDA= b00 +b01D+b02D2 + b10 +b11D+b12D2 +
b20 +b21D+b22D2+
b30 +b31D+b32D2
y el SIDA es ahora una función del tiempo que puede variar o “moverse" en el espacio geográfico con los cambios en la densidad de población. Es de notar, conceptualmente, que tenemos un proceso espacial muy general cuya expresión específica está condicionada por las particularidades del lugar. De este modo dos antiguos conceptos geográficos, espacio y lugar, que tradicionalmente han marcado perspectivas en ocasiones bastante antagónicas en la geografía, aparecen juntos en un maridaje metodológico armonioso.
Después de las normales estimaciones de los mínimos cuadrados de los parámetros, el ajuste de tales modelos de expansión para la epidemia de SIDA es bastante alto (normalmente alrededor de r -0,90) y puesto que la densidad de población (D) permanece relativamente estable con el paso de los años, podemos sustituir por tiempos futuros (T) para predecir el siguiente o los siguientes mapas de SIDA. Nótese, sin embargo, que estamos confrontando el problema geográfico general de la exploración de la estructura de una serie espacio-temporal, intentando extraer toda la información posible para computar el futuro a partir de nuestra experiencia del pasado. Desde un punto de vista ético, por supuesto. estamos haciendo esto para intentar que nuestras predicciones no se cumplan. En un sentido computacional hemos visto el futuro en las dimensiones fundamentales de espacio y tiempo de la existencia humana, y no nos gusta lo que vemos. Si estas predicciones se pueden usar en secuencias cartográficas animadas para la televisión educativa, y para llevar a la gente (particularmente adolescentes y adultos jóvenes) a que consideren el SIDA como un riesgo para la salud directo y personal, entonces nuestro mayor éxito seria ver fracasar nuestras predicciones. Dicho esto. y creemos que es importante decirlo, sigue en pie el problema general de la predicción del siguiente mapa.
Para calibrar la expresión terminal final de la ecuación de expansión usamos mínimos cuadrados ordinarios a veces con unas pocas restricciones añadidas, y utilizando un método de reducción para eliminar la potencial colinealidad degradante. Pero, en cierto modo, estamos echándolo todo en el mismo saco cuando calibramos los parámetros en un conjunto de datos específicos. En otras palabras, no importa cuál sea la estructura espacial en un punto u otro o si es fuerte o débil, de todos modos encaja en el proceso do calibración. Pero podía ocurrir que en algún área y en un momento determinado, hubiera habido un grado muy alto de estructura espacial (implicando un alto grado de previsibilidad espacial), mientras que en otro área no hubiera habido virtualmente ninguna estructura espacial, sino sólo el equivalente geográfico del “ruido blanco" o valores aleatorios (no implicando ninguna previsibilidad espacial). Lo que realmente necesitamos es un enfoque metodológico más refinado, un pequeño “sabueso" funcional que podamos soltar en el espacio geográfico para que rebusque la estructura espacial local y nos diga cuándo la ha encontrado. En áreas donde haya emergido un alto grado de estructura espacial en el curso de la epidemia de SIDA, los parámetros de nuestro sabueso se alejarán del cero significativamente, y ladrará con fuerza, diciéndonos ¡Mira! ¡Aquí, en esta región, podemos hacer buenas predicciones!" Y a la inversa, donde no haya estructura espacial disponible, donde no haya información espacial presente en el mapa, nuestro sabueso pasará de largo silencosamente para explorar algún otro lugar. Hemos llegado a la filtración adaptativa espacial y al rastreo paramétrico (“parametric tracking”) en el tiempo.
Filtración adaptativa espacial
La filtración adaptativa espacial es una forma específicamente geográfica de una amplia clase de modelos caracterizados por la habilidad de sus parámetros de alterarse o adaptarse en diversos dominios de estudio tradicionalmente en el tiempo. En el ámbito del tiempo, al que perversamente confinan su pensamiento los epidemiólogos, intentamos encontrar estructura en una serie temporal y luego usarla para predecir los valores temporales en el futuro. Son formas comunes el ajuste exponencial ("exponential smoothing"). los modelos de medios dinámicos autorregresivos (“autoregressive moving average models"), los filtros de Kalman y los filtros de adaptación. Una expresión general sería:
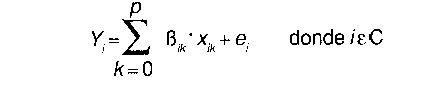
Específicamente:
|
SIDA en Condado i |
Parámetro k para el condado i |
Variable independiente para el condado i |
Un factor de error |
Una serie de “cortes” temporales o una serie de “condados” |
En nuestra investigación sobre el SIDA usamos la siguiente ecuación, en la que POP significa población:
SIDAi - b0+ b1 (POP) + b2 (POP))2
aunque para nuestro ejemplo, manipulado para un uso esencialmente pedagógico, no usaremos el término cuadrático para evitar un exceso de aritmética.
Este es nuestro “filtro espacial", y nos gustaría adaptar sus parámetros b0, b1 y b2 a las condiciones locales de una región en un período de tiempo determinado. Hay que recordar que en la filtración adaptativa espacial mantenemos el tiempo constante, pero tratando de hacer que el filtro (aquí una ecuación de segundo grado) se adapte usando la estructura espacial local, es decir, los valores alrededor del condado i, o quizás contiguos a él. Se podría preguntar cómo entra el tiempo en la predicción del siguiente mapa. Lo hará, pero dejaremos esta pregunta de lado por el momento.
En un filtro de adaptación espacial necesitamos tener alguna manera de forzar o corregir los parámetros del condado i de modo que produzcan una predicción que converja en el valor conocido, o en el verdadero. Esto significa:
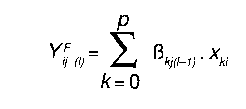
|
predicción de SlDA [YFij (I)] en la iteración (I) en el condado i a partir de un conjunto de condados que lo rodean (contiguos) |
ß0+ ß1 (POP) + ß2 (POP)2 Todos los parámetros son para los condados contiguos de la iteración anterior (I-1) |
Al comenzar a usar la filtración adaptativa espacial a menudo encontramos contuso el proceso iterativo. Por ello consideramos importante ponerlo de manifiesto con un ejemplo elaborado por nosotros. A estas alturas. tenemos un conjunto de predicciones computadas para el condado cada una de ellas producida por os parámetros de los filtros de adaptación espacial que caracterizan el conjunto circundante de condados contiguos. Pediremos al lector un poco de paciencia por ahora, ya que dentro de poco resolveremos las operaciones aritméticas de las dos primeras iteraciones. La filtración adaptativa espacial (SAF) es en esencia muy 5 mple, y está llena de conceptos e implicaciones geográficas, pero hay mucho a “tener en cuenta", al mismo tiempo, y cuando se emplea por primera vez parece mucho más difícil de lo que es realmente. Las computaciones son extremadamente repetitivas, pero esto es exactamente lo que se les da bien a los ordenadores, y ya veremos cómo lleva a los nuevos y rapidísimos ordenadores paralelos (aunque estos requieren unas técnicas de programación especiales, y no son necesarios para usar la SAF).
Volviendo a nuestro ejemplo... tenemos un conjunto de predicciones (personas con SIDA) para el condado basadas en los parámetros de los SAFs de los condados circundantes, generalmente contiguos. Usamos estos valores previstos o predichos para computar un conjunto de parámetros nuevo o actualizado para el condado i, empleando lo que es, en esencia, un pequeño bucle de realimentación negativa, que podemos expresar así:
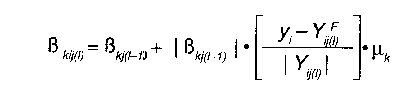
O, en la lengua de Cervantes mejor que en la de Galileo:

Mejor que soltar ahora un montón de ecuaciones algebraicas será recurrir directamente a un pequeño ejemplo. Supongamos que tenemos una región pequeña dividida en cinco condados A, B, C, D y E. Para el ordenador, podríamos describir fácilmente sus relaciones de contigüidad con una matriz de contigüidad 0,1 que reflejara la misma información que el gráfico.
Supongamos que en un momento dado cualquiera las poblaciones y has víctimas de SIDA son como sigue:
| Condado | Población | Víctimas de SIDA |
| A | 6 | 3 |
| B | 4 | 3 |
| C | 14 | 11 |
| D | 10 | 9 |
| E | 18 | 17 |
Para acometer la búsqueda de los mejores parámetros para el filtro espacial de cada condado tenemos que empezar con una estimación aproximada cuyos parámetros puedan variar y adaptarse localmente para dar predicciones cada vez mejores. Generalmente empezamos con una estimación global, usando todos os condados y relacionando los casos de SIDA con la población, o que nos dará los valores paramétricos iniciales a través de los mínimos cuadrados. De este modo, sólo por, la primera iteracion, cada condado tiene un filtro que es igual a todos los demás. Para nuestros propósitos usaremos:
SIDA = -2 + l (POP)
Obsérvese, una vez más, que no incluimos el término cuadrático para simplificar las cosas.
Si usamos esta ecuación global inicial para el filtro de cada condado, podemos estimar el número de gente con SIDA a partir de la población de un condado, comparar ese cálculo aprnxtmativo con el número real y de este modo computar el error o desviación del modo siguiente:
| Condado | Víctimas reales de SIDA | Víctimas previstas de SIDA | Desviación |
| A | 3 | 4 | -1 |
| B | 3 | 2 | +1 |
| C | 11 | 12 | -1 |
| D | 9 | 8 | +1 |
| E | 17 | 16 | +1 |
Podemos usar como indice de error total o bien la suma de los valores absolutos de las desvaciones, o la suma de los cuadrados (en este caso en particular ambas coinciden).
Suma de los valores absolutos de las desviaciones = 5
Suma de los cuadrados de las desviaciones = 5
Lo primero que tenemos que nacer es usar los filtros de cada uno de los condados j contiguos para hacer una estimación del SIDA en el condado i. Recordemos que, en esta primora iteración, el filtro de todos los condados es el mismo, SIDA = -2 + l (POP), no obstante lo cual tendremos que computar cada uno dolos pasos de proceso, aunque resulte algo repetitivo y tedioso. Nuestra intenctón es llevar al lector al punto en que él mismo pueda programar el software apropiado para su propio ordenador local
Empezamos con el condado A, que tiene como condados contiguos D y E. Así, usando la población del condado A, con los parámetros ß0 y ß1 de D y E tenemos:
SIDA(A<-D) = -2 + 1(6) = 4
SlDA(A<-E) = -2 + 1(6) =
Dado que todos los parámetros de los filtros de los condados son iguales (ß0 = -2, ß1= 1) al comienzo de la primera iteración, el proceso da la sensación de simplista, pero hemos de recordar que las dos previsiones para A están usando los parámetros de D y E respectivamente.
Ahora tenemos que ajustar o adaptar los parámetros del condado A, ß0 primero y después ß1, para obtener una estimación mejor, basada en los contiguos D y E. Aquí es donde aparece la pequeña epresíón de la realimentaoión negativa:
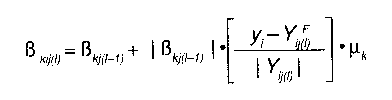
Una vez más, vamos a ajustar el parámetro kº (k = 0) del condado i (i = A) a partir del condado j (j = D y E) en la primera iteración I = 1). Así
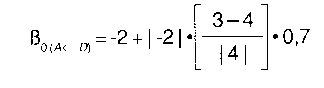
Detengámonos ahora a tomar en consideración un par de cosas. Primero, qué pasa con ese factor amortiguador µ0 = 0,7? ¿Cómo lo hemos encontrado? Obviamente el valor particurar de µ0 que estará entre 0 y 1 alterará o "amortiguará" el ritmo a que la realimentación negativa adapta el parámetro ß0. No tenemos ningún modo a priori de determinar cuál será este valor, por lo que en realidad realizamos una búsqueda combinatoria, o secuencial, probando todas las combinaciones de

y así sucesivamente
En este caso probaríamos nueve valores de µ0 combinados con nueve valores de µ0, es decir, 81 posibilidades, escogiendo la combinación que redujera la desviación total al final de una serie completa de iteraciones. En el caso de nuestro filtro cuadrático. esto significa que realizamos el problema completo 9 x 9 x 9 = 729 veces. La filtración adaptativa espacial necesita un ordenador potente y rápido, o quizás un ordenador personal al que se pueda dejar trabajando solo durante una semana. Para Pensilvania, con 67 condados, ocho años, un filtro cuadrático y una búsqueda secuencial de 729 combinaciones posibles de µs el problema entero llevó aproximadamente 30 segundos en una unidad informática principal de grandes dimensiones que trabajaba secuencialmente. Hay que observar que si los parámetros de los filtros espaciales no varían de un lugar a otro (es decir. si la relación entre SIDA y población es la misma en todas partes), los factores amortiguadores µk serán todos cero. En otras palabras, no es necesario ningún ajuste con realimentación negativa. En el sencillo ejemplo que estamos utilizando aquí, asumimos por el momento que hemos llegado a los valores particulares µ0 = 0,7 y µ9 = 0,l.
En segundo lugar, y en este primer ejemplo.
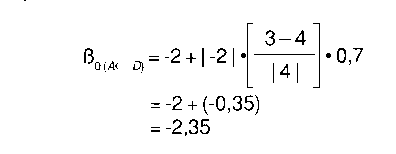
El valor previsto de cuatro personas con SÍDA era demasiado alto comparado con el valor real de tres, por lo que rebajamos el nuevo valor de ß0 para que el valor previsto se aproxime al real. Ovbiamente el ritmo al que las previsiones convergen con los valores reales dependerá de (1) los parámetros de los filtros en los condados contiguos y (2) el factor amortiguador µk, pero ya discutiremos más tarde la cuestión de la convergencia en detalle.
Volviendo a nuestro ejemplo, tenemos ahora que ajustar el ß0 del condado A para que permita la influencia de E. Sólo en esta primera iteración será el mismo.

Promediamos estos dos valores ajustados de ß0 del condado A basados en D y E, con lo que al final de la iteración l tenemos:
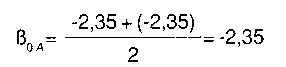
Ahora hacemos exactamente lo mismo para ß1. Por ejemplo,
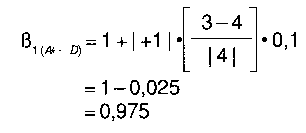
y

que dan un promedio
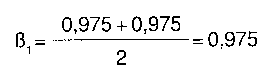
Obsénvese. una vez más, que como nuestra predicción de 4 era demasiado alta el proceso de realimentación negativa amortiguada ha reducido la estimación de ß1. Así, ahora, al final de la primera iteración, el filtro del condado A tiene los parámetros siguientes:
SIDAA -2,35 +0,975 (POP)
En otras palabras, se ha ajustado o adaptado de alguna manera a sus propias condiciones locales en la región.
Antes de continuar, queremos llevar su atención hacia un problema computacional pero también completamente geográfico. En el terreno puramente intuitivo, si la "superficie" de SIDA es bastante uniforme (un paisaje humano "liso'!), el tipo de superfice que un matemático describiría como "de buen comportamiento", podríamos esperar que los parámetros de los filtros espaciales en los condados cercanos o contiguos predijeran los casos de SIDA de un condado en particular bastante bien. En general, las cosas próximas en el espacio geográfico tienden a ser bastante similares. Esto sería el equivalente en un análisis de una serie temporal, a usar valores que cambian de modo uniforme en el pasado para adaptar una estimación de un filtro a un valor conocido en el presente. Sin embargo, si una superficie de SIDA es muy irregular (un pico exponencial de SIDA alto en una ciudad está al lado de un condado rural de baja densidad), los parámetros del filtro para la "punta" urbana no predecirán muy bien las víctimas SIDA en el condado rural. Esto significa que en nuestra realimentación negativa la diferencia entre el número real de víctimas de SIDA (YF) y el valor de predicción (YFij(I)) será grande y puede que corrija o adapte por exceso los valores de ß. Retomaremos y resolveremos este problema más adelante con mayor detalle, pero una solución simple es decir que "si el término completo de realimentación negativa excede, digamos, 0,5, entonces se ha de utlizar en su lugaro 0,5 (o algún otro término arbitrario menor)". En este ejemplo no hemos usado una regla de este tipo deliberadamente, ya que queremos plantear la cuestión de la convergencia de modo más explícito nás adelante (ver el final de la iteración 2).
Ahora hacemos exactamente lo mismo para los condadosB,C, D y E. Simplemente como dos ejemplos de trabajo más, y adaptando primero el ß1 del condado C a partirde los condados contiguos B. D y E, tenemos:

y, todavía en esta primera iteración,
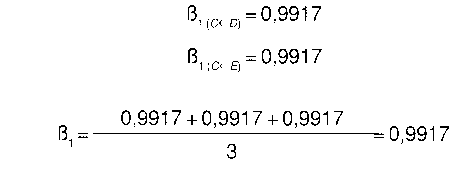
Sólo a modo de segundo ejemplo, bastante arbitrario adaptaremos el ß0 del condado Da partir de A, B, C, y E, con lo que tendremos:

y lo mismo para ß0(D<--B), ß0(D<--C) y ß0(D<--E) Lo que da un promedio de
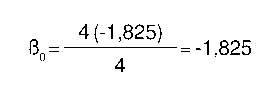
Obsérvese que en oste caso el valor de prodicción era menor que el real, con lo que la realimentación negativa elevó el valor de ß0.
Con estos ejemplos delante, queda como tarea para el lector computar todos los otros valores de los parámetros tras la primera iteración. Esto se puede hacer con una calculadora de bolsillo, y aunque es un poco tedioso, sí parece una buena manera de meterse en profundidad en el proceso de la filtración adaptativa espacial. Cuando haya acabado, puede resumir todos los parámetros adaptados en una tabla como ésta:
Parámetros tras la iteración 1
| Condado | ß0 | ß1 | Expectativas de SIDA | Desviación (Real-Esperada) |
| A | -2,3500 | 0,9750 | 3,5000 | 3-3,5000= -0,5000 |
| B | -1,3000 | 1,0500 | 2,9000 | 3-2,9000= +0,1000 |
| C | -2,1167 | 0,9917 | 11,7671 | 11-11,7671= -7611 |
| D | -1,8250 | 8,3000 | 8,3000 | 9-8,3000= +0,7000 |
| E | -1,9125 | 16,2009 | 16,2009 | 17-16,2009= +0,7991 |
Desviación absoluta = 2,8662 (antes 5)
Desviación al cuadrado = 1,9770 (antes 5)
Obsérvese que, como resultado de haber permitido que los parámetros de nuestros filtros espaciales se adaptaran localmente, estos producen ahora estimaciones más cercanas a los valores reales, produciendo así las desviaciones absolutas y al cuadrado. Hasta ahora, el proceso de iteración parece haberse do todo un éxito.
Queremos hacer notar, de pasada, que tras un análisis completo usando la filtración adaptativa espacial, el trazado de los ß0s, ßs, y ß2s para cada condado en tres mapas puede dar como resultado unos descubrimientos sugerentes. En tanto en cuanto los parámetros son distintos de cero, los mapas nos dicen dónde hay estructura espacial simple lineal y no lineal. Esto se puede interpretar como las regiones del mapa en que se pueden hacer predicciones de gran precisón, e, igualmente, las regiones donde podemos esperar predicciones de poco valor. Hacer mapas de este tipo durante una serie de años nos permite ver dónde emerge primero la estructura espacial, y después cómo se fortalece con el tiempo.
Volvemos ahora a nuestro ejempio, empezando ya con la segunda iteración. Debemos tener más cuidado al trabajar en esta segunda fase, ya que ahora cada condado tiene su propio conjunto de parámetros como resultado do haber adaptado el conjunto global, o inicial a las condiciones locales.
Empezamos con el condado A, contiguo a D y E, usando los parámetro de D y E con la población del condado A para predecir los casos de SIDA de A. Así:
SIDA (A-D)= 1,8250 + 1,0125 (6)
D's ß0 D's ß1 (A's Población)
= 4,2500
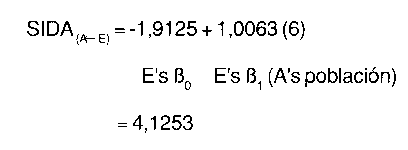
Y sustituyendo por estas dos diferentes estimaciones de SIDA en el condado A, basadas en los parámetros actuales del filtro espacial en D y E tenemos
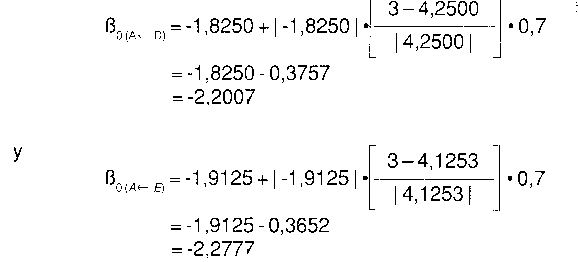
Y para obtener nuestra nueva estimación del ß1 del condado A tomamos la media de las dos estimaciones basadas en D y E, es decir:

Ahora hacemos exactamente lo mismo para el S del condado A:

Y tomando la media, como hemos hecho anteriormente

Con lo que ahora los parámetros del condado A, tras la segunda iteración, dan un filtro adaptativo espacial de:
SIDAA = - 2,2392 + 0,9808 (POP)
Una vez mas, el lector está en condiciones de computar con una calculadora de bolsillo los parámetros de los otros filtros espaciales para los condados B, C, D y E. Como vimos anteriormente, ésto no sólo es el mejor modo que conocemos de llegar a una comprensión de la filtración adaptativa espacial que no sea meramente formal, sino también de llegar a sentir de un modo cercano y práctico lo que ocurre en realidad. Es la diferencia existente entre el conocimiento proposicional (el que se aprende símpemente con los libros) y el conocimiento tácito (que sólo se puede obtener haciendo cosas, como si se tratara do un aprendiz). Cuando haya acabado los cómputos para los otros condados, podemos elaborar otra tabla al final de la segunda iteración que quedaría así:
Parámetros tras la iteración 2
|
Condado |
ß0 |
ß1 |
Expectativas de SIDA |
Desviación (Real-Esperada) |
|
A |
-2,2392 |
0,9808 |
3,6456 |
-0,6456 |
|
B |
-1,2879 |
1,0506 |
2,9145 |
+0,0855 |
|
C |
-1,8231 |
1,0097 |
12,3127 |
-1,3127 |
|
D |
-1,7440 |
1,0180 |
8,4360 |
+0,5640 |
|
E |
-1,9770 |
1,0008 |
16,1670 |
+0,8330 |
Desviación absoluta = 3,4408 (antes 2,8662)
Desviación al cuadrado = 3,1593 (antes 1,9770)
Pero obsérvese lo que ha ocurrido. Como resultado de la segunda iteración, las desviaciones en realidad han aumentado, lo que significa que, para el "sistema" como un todo, los parámetrosde nuestros filtros de adaptación espacial son peores do lo que eran anteriormente.
Antes de que cunda el pánico, cayendo en la desesperación de los antiguos pitagóricos al descubrir los números irracionales, deberíamos aclarar que hemos elaborado deliberadamente un ejemplo como éste con fines pedagógicos, porque plantea una serie de importantes cuestiones técnicas y geográficas. La primera es el tema de la convergencia, y si nuestro proceso iterativo convergerá uniforme y eficientemente al conjunto de parámetros para todos nuestros filtros que minimizarán sistemáticamente las desviaciones, las diferencias entre los valores deSIDA y los estimados (esperados). Obviamente, la convergencia no es necesariamente uniforme: nuestro ejemplo deja ver claramente que tratar de encontrar el mejor conjunto de parámetros puede llevarnos por un camino accidentado. En general, no obstante, el proceso de realimentación negativa garantizará una tendencia de convergencia en torno a a cual las iteraciones individuales pueden quedar un poco por encima o por debajo.
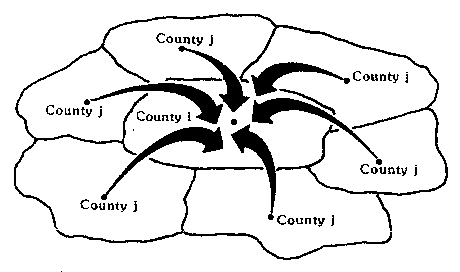
¿De qué depende la oonvergencia al mejor conjunto de parámetros? De dos cosas: el conjunto de factores amortiguadores µkl que se encuentran a través de la búsqueda combinatoria secuencial y el comportamiento (en el sentido matemático) de la superficie de población (o de SIDA) Obsérvese que tras la segunda iteración las desviaciones individuales de los condados que más contribuyen a los factores de error generales son las de los condados D y E. Justamente los condados con mayor población y más alto número de víctimas de SIDA. No son exactamente las "puntas" exponenciales que a menudo vemos en las superficies de geografía humana, pero son relativamente grandes comparados con los condados "rurales" adyacentes, A y B. Esto quiere decir que los parámetros del, digamos, "condado urbano" E, al final de la iteración 1, pueden no ser muy buenos indicadores del "condado rural" A y viceversa. De hecho, si el lector revisa cuidadosamente sus computaciones condado a condado, y compara las iteraciones 1 y 2, verá que hay a veces una considerable compensación por exceso. En cierto sentido, un condado "rural" y otro urbano que sean contiguos pueden hacer "saltar las estimaciones de los parámetros hacia atrás y hacia adelante, produciendo así el "·camino accidentado" en el proceso de convergencia. Por supuesto, algunos de los "altibajos" serán amortiguados por el conjunto de factores amortiguadores µk más apropiado, en un modo muy similar a como unos buenos amortiguadores en un coche atenúan el efecto de los baches en una mala carretera Sin embargo, esto plantea una vez más la cuestión de cuáles son exactamente los mejores valores que podemos usar.
Sería casi imposible responder a esto con una calculadora de bolsillo porque tendríamos que acometer la búsqueda combinatoria secuencial de 81 posibies valores de µk a mano. De hecho hemos introducido el problema en un ordenador, descubriendo que los valores µ0= 0,9 y µ1=0,8 producen una convergencia bastante uniforme, con lo que tras 13 iteraciones la desviación absoluta se reduce a 1,028, con los parámetros siguientes:
Parámetros que producen el mínimo error
(µ0 + 0.9, µ1 = 0.8)
|
Condado |
ß0 |
ß1 |
Expectativas de SIDA |
Desviación (Real-Esperada)
|
|
A |
-1, 870 |
0,723 |
2,5 |
-0,53 |
|
B |
-1,229 |
1,131 |
3,3 |
-0,29 |
|
C |
-1,581 |
0,904 |
11,1 |
-0,08 |
|
D |
-1,359 |
1,043 |
9,1 |
-0,08 |
|
E |
-1,384 |
1,024 |
17,1 |
-0,05 |
| Desviación absoluta |= 1,03
Desviación al cuadrado = 0,38
Obsérvese, simplementecomo un dato aparte, que estos factores amortiguadores están lejos del cero, lo que indica que un alto grado de estructura espacial está presente incluso en este pequeño ejemplo pedagógico.
Pero hemos de confesar que al extraer estas estimaciones con un ordenador, hemos hecho también algo más que tiene en cuenta el "comportamiento" de la superficie de población, el segundo factor que recordemos, puede afectar el proceso de convergencia. Antes, cuando estábamos realizando las operaciones aritméticas de la primera y segunda iteraciones, computamos las estimaciones revisadas de un parámetro para el condado a partir del conjunto de condados contiguos j, para promediarlas después. El proceso promediador ordinario que seguimos ponderaba todas las estimaciones de los condados contiguos por igual, aunque podemos ver que algunos de los condados (esencialmente aquellos bastante similares al condado j en este punto del proceso iterativo) nos ayudan a obtener mejores estimaciones revisadas en la iteración sugiente, mientras que otros (aquellos no similares al condado i) "inyectan" sus bastante pobres estimaciones en el proceso promediador. ¿Por qué no usar entonces esta nformación para mejorar nuestra estimación media final? Todo lo que hay que hacer es ponderar cada término o estimación en nuestro proceso promediador inversamente a la cantidad de error a que induce. De este modo las estimaciones buenas a partir de algunos de los condados j tendrán mucho peso, mientras que las malas tendrán poco.
Ilustraremos esto punto asumiendo que hemos llegado a la iteración 13 en nuestro proceso de convergencia. con µ0 = 0,9 y µ1= 0,8. y que vamos a calcular los parámetros de filtro del condado C a partir de los condados contiguos B, D y E. Como hemos hecho anteriormente, usamos los parámetros (obtenidos en la iteración 12 anterior) de B, D y E con la población de C para calcular el SIDA de C:
SIDA0 B = 1,2407 + 1,1401 (14)
= 14,7207 (Real = 11;Desviación = -3,7270)
SIDA0 D = -1,3808 + 1,0463 (14)
= 13,2674 (Real = 11; Desviación = -2,2674)
SIDA0 E = -1,4100 + 1,0259 (14)
= 12,9526 (Real = 11; Desviación = -1,9526)
Como se puede ver, en esta iteración en particular la estimacion de SIDA en C a partir del condado contiguo B produce el mayor error o desviación (-3,7207). seguido de D (-2,2674) y luego de E (-1,9526). Cuando computemos por fin los parámetros nuevos para el filtro de C como un promedio de todas las estimaciones obtenidas de B, D y E. ¿Como podremos ponderar las tres estimaciones inversamente a estas desviaciones? Computamos primero el porcentaje con que contribuye cada una como sigue
|
-3,7207 |
0,4686 |
|
-2,2674 |
0,2855 |
|
-1,9526 |
0,2459 |
|
|
|
y después calculamos la media ponderada inversa:
|
1/0,4686 = 2,1340 |
0,220 medida para B |
|
1/0,2855 = 3,5026 |
0,361 medida para D |
|
1/0,2459 = 4,0667 |
0,419 medida para E |
|
|
simplemente a modo de ejemplo, comuptaremos el ß0 del condado C como sigue:
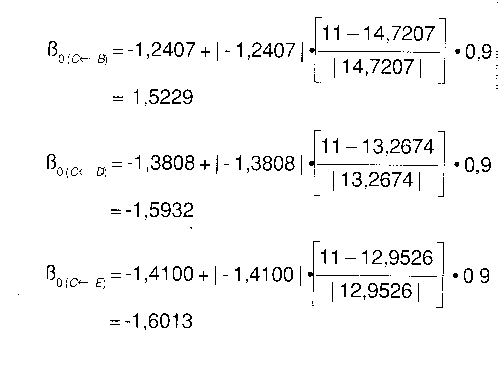
Ahora, si promediáramos estos valores de la manera habitual tendríamos simplemente:
|
-1,5229-1,5932-1,6013 = 1,5725 ___________________________ 3 |
Pero con nuestros coeficientes de ponderación inversa, la nueva estimación del ß0 de C es:
(-1,5229 x 220) +(-1,5932 x 361) + (-1,6013 x 419) = 1,5810
lo que está en concordancia con el valor que hemos reflejado en la tabla anterior.
Cuando se presentan todas estas computaciones, la filtración adaptativa espacial parece muy complicada y pesada. Do hecho, la idea básica, como muchas de las ideas de la ciencia es bastante simple. Dejamos que nuestros filtros espaciales se adapten a las condiciones locales para producir la desviación más baja, sólo l,03 en nuestro ejemplo final, comparado con el 5,00 con el que empezamos. Esto representa una mejora del 79%, lo que ofrece buenos augurios para nuestro objetivo de predicción final. Sin embargo, esto plantea ora vez la cuestión del tiempo. Pero antes de que lleguemos al aspecto "temporal" de las series espacio-temporales, todavía nos quedan dos importantes cuestiones "espaciales", una técnica y otra totalmente geográfica.
La primera, la técnica, conlleva el tema de una "regla de parada". Cuando estamos llevando a cabo nuestra búsqueda secuencial entre el conjunto de factores amortiguadores µ ¿cuántas iteraciones habremos de usar antes de decidir terminar una ejecución en particular?. Tonemos un cierto número de posíbilidades. Ninguna de ellas es enteramente satisfactoria para el más purista de los matemáticos, pero que resultan suficientemente útiles en términos aplicados y prácticos.
Hemos descubiento que si computamos el error absoluto medio, o:
|
Test
(1) =
______________________ N |
al final de cada iteracion entonces tendremos una buena regla de parada cuando
|
|Test (I-1) - Test (I)| <0,01 |
En segundo lugar, está el problema de cuál de los conjuntos de condados j contribuye a la revisión de un condado i concreto en estudio. A partir de nuestro pequeño ejemplo, está claro que sólo los condados j inmediatamente contiguos al condado i influyen en la revisión de los parámetros en la primera iteración. Pero obsérvese que en la segunda iteración, los parametros de estos condados contiguos han sido revisados por todos sus condados contiguos,(incluyendo, claro está, el condado j) en la iteración anterior, con lo que en cierto sentido los condados que se encuentran a "una distancia de dos contiguidades" están haciendo su contribución.. y así sucesivamente para cada iteración subsiguiente. Sin embargo, si la influencia de un condado j en el condado i es amortiguada por µ en la primera iteración, la intluencia de la contigüidad estará amortiguada dos veces por µ. µ o µ2 en la segunda... y así sucesviamente, produciendo un efecto de disminución exponencial en el espacio geográfico estructurado por la relación de contiguidad.
El efecto de contigüidad plantea una de las cuestiones de naturaleza puramente geográfica más importantes. Es simplemente: ¿qué cuenta en realidad como contigüidad? ¿será contigüidad en el espacio un espacio SIDA o de "interacción humana” convenientemente transformado? Recordemos que pudimos usar un planteamiento del modelo gravitatorio como una transformación, llevando el mapa convencional de Ohio a un espacio multidimensional en el que las grandes ciudades estarían juntas en el cero, y las áreas rurales serían empujadas a la periferia de la nube rmultidimensional de puntos que representa a cada condado. ¿Quizás Cleveland, Columbus y Cincinnati están en realidad próximas, es decir, son en cierto modo contiguas"? ¿Quizás Pensilvana.Filadelfia y Pittsburg están puerta con puerta? ¿Quizás en España Madrid es vecina de Barcelona, Sevilla. Valladolid y Zaragoza?
¿Qué implicaría esto para la filtración adaptativa espacial? Si definimos la matriz de contigüidad a partir de una distancia de separación en el espacio SIDA transformado. los parámetros de. digamos Filadelfia pueden calcularse muy bien a partir de los de Pittsburg y otras grandes ciudades. En España, por ejemplo, podríamos calcular los parámetros de Sevilla a partir de los de Madrid Esto podría reflejar exactamente las rlpaciones y las interacciones en geografía humana captadas por la transformación del modelo gravitatorio. De este modo, la estructura subyacente de interacción humana, necesaria para defender la existen cia del tráfico de VFH y su transmisión mesogeográfica entra ahora de modo explícito en la descripción del problema y en las computaciones de los filtros de adaptación espacial.
Pero podemos ir todavía más lejos, gracias al ordenador y el poder de búsqueda que ahora nos confiere. Conceptualmente, podemos pensar en transformar el espacio, buscando así la matriz de contigüidad más apropiada que reduzca la desviacion global. Pero en la práctica no es necesario. En lugar de especificar a priori la matriz de contigüidad, ya sea en el espacio geográfico convencional o en un espacio SIDA o de interacción transformado, podemos limitarnos a pedir al ordenador que examine todos los condados y después ordenar aquellos cuyos parámetros dan las mejores estimaciones de SIDA en el condado i en estudio. El conjunto de condados j que ocupan un puesto elevado serán aquellos más similares al condado i por su estructura espacial, una semejanza estructural reflejada en los parámetros que dan buenas predicciones de SIDA en el condado i. De este modo, los condados j más similares al condado i deberían ayudarnos a revisar de modo eficiente los parámetros que varían y se adaptan espacialmente. Obsérvese que e conjunto de, digamos, los cinco "mejores" condados no tiene por qué ser el mismo en cada iteración, aunque podría resultar sugerente interpretar esbs conjuntos de condados j para cada condado cuando hayamos encontrado por fin las mejores estimaciones que minimicen ladesviación absoluta. ¿Qué nos revelarían acerca de la geografía humana de la región vista desde la perspectiva particular de la epidemia de SlDA? ¿Serían secciones de estructuras de homosexuatidad y de drogadicción intravenosa, "paisajes de interacción" invisibles que quedarían al descubierto con estas sonsibles metodologías geográficas? De modo similar,estos mejores "conjuntos" finales pueden no ser los mismos de un año a otro, ya que la dinámica espacial" del proceso de difusión reestructura el espacio en que se difunde el SIDA. Una vez más, esto trae a colación el asunto de! tiempo, y debemos en este punto tratarlo do modo expplicito haciendo notar que la filtración adaptativa espacial tiene mucho que ver con la geogratía.
Rastreo paramétrico
En su primer contacto con la filtración adaptativa espacial la gente puedo pensar que quizas los geógrafos se hayan vuelto locos. "Por qué, se preguntan quieren que los parámetros de sus filtros espaciales se adapten para dar buenas estimaciones del numero de víctimas de SIDA cuando ya saben el número real de éstas? ¿Por qué intentar calcular algo que ya se sabe?. De hecho. ese pequeño bucle do realimentación negativa suyo exige que se sepa el número real antes de empezar ¿Cómo pueden afirmar que están haciendo la predicción del próximo mapa y los subsiguientes? ¿Cómo entra el tiempo en todo esto? ¿No será la pescadilla que se muerde la cola? Y claro está, a estas alturas la sospecha de que estamos locos tiene que aparecer, ya que hemos utilzado un solo plano temporal, un mapa, en nuestras series espacio temporales, y hemos permitido que nuestros filtros espaciales (o sabuesos funcionales) adapten sus parámetros para reflejar solamente la estructura espacial. El tiempo, de hecho, se ha mantenido constante. Pero supongamos ahora que tomamos todos los cortes tempora es en nuestras series espacio-temporales (s y, t) y ejecutamos la filtración adaptativa espacial en cada uno de los mapas Ahora podemos preguntar para cada condado ¿Muestran los parámetros de los filtros espaciales alguna tendencia o regularidad en el tiempo?.' En otras palabras. ¿podemos rastrear los parámetros de los filtros espaciales en el tiempo y ver si los ß0, ß1 y ß2 de un condado muestran un comportamiento uniformo, regular y consecuentemente previsible? Después de todo esto es lo que podíamos esperar si simplemente mirásemos una secuencia de mapas que muestren la difusión de SIDA en el tiempo Como hicimos notar anteriormente, el mero hecho de que podamos hacer una buena conjetura sobre el mapa siguiente basándonos sólo en la intuición significa que tenemos fuertes expectativas sobre la regularidad del cambio espacial en el tiempo. Es precisamonte este cambio geográfico regular en el mapa lo que se debería reflejar en el cambio paramétrico uniforme de nuestros filtros de adaptación.
Para dejar claro este punto en nuestro pensamiento. probemos a considerar lo contrario. Supongamos que los parámetros de nuestros filtros de adaptación espacial no cambiarán uniformemente en el tiempo (lo que implicaría por ejemplo que ß0, ß1 y ß2 no serían simples funciones de t, sino que más bien saltarán en un modo complejo, incuso caótico. Esto ocurriría en un proceso que fuera totalmente aleatorio en el tiempo y el espacio. Los parámetros do un mapa adaptados espacialmente en un tiempo t no tendrían relación alguna con aquellos del mapa en t + 1, t + 2, etc. No habría ningún orden ni estructura en nuestra serie espacio temporal, y por tanto no habría ninguna posibilidad de predecir lo que pudiera ocurrir en el futuro. Es difícil imaginar qué tipo do fenómenos podrían ser caracterizados por una serie así.
¿O quizás no?. Tomemos en consideración un problema de la geografía física, ya que la prediccion del mapa siguiente es un problema muy general, no confinado a fenómenos humanos. Supongamos que quisiéramos predecir el grosor y extensión del hielo ártico por las obvias implicaciones que puede tener para la Tierra, el albedo, su capacidad energética, el clima, etc. Sabemos que ha habido abundantes mediciones al cabo de muchos años del grosor del hielo, formando una serie espacio-temporal. La filtración adaptativa espacial y el rastreo paramétrico podrían examinar el grado de predictabilidad de un lugar a otro en todo el casquete polar ártico En ciertas regiones el grosor del hielo podría predecirse con una precisión considerable mientras que en otras áreas podría ser imprevisible. Pero incluso esta información merecería nuestro interés. Por ejemplo, tenemos inmensas espirales y remolinos de agua tropical templada surgiendo de la Corriente del Golfo aparentemente al azar es decir, de un modo caótico o imprevisible. Estos haces de energía fluyen en dirección norte hasta las regiones árticas y traen como consecuencia la extensión y grosor de hielo a lo largo de los bordes. Si estas dos variables (extensión y grosor) no se pueden predecir los parámetros de los fítros espaciales en estas regiones mostrarán también un comportamiento aleatorio en el tiempo, indicando que nuestro conocimiento geográfico en un momento dado no nos ayudará a predecir una distribución geográfica en otro momento. De hecho, podríamos incluso pensar en elaborar un mapa hipsométrico de "isopredictores", quizás con curvas altas en el centro del casquete polar ártico y bajas en los bordes. O quizás no ... ¿Quién sabe? Gradualmente nos vamos dando cuenta de que hay fenómenos caóticos en todas partes del mundo físico, lo que mplica que en ciertas escalas geográficas y temporales no tenemos ninguna posibilidad de predecir nada. Incluso los planetas, esas maravillas de precisión en la mecánica celeste de Isaac Newton, son caóticos, y consiguientemente imprevisibles, a lo largo de escalas temporales largas. Todo lo que podemos hacer es observar los sistemas físicos y humanos e intentar predecir las configuraciones en el espacio (geografía) y en el tiempo (historia) como mejor nos permitan nuestros conocimientos científicos. En este esfuerzo general, la filtración adaptativa espacial tendrá que desempeñar un pequeño, poro quizás importante papel.
Relaciones con otras investigaciones científicas
Algunas ideas que se ven en último término como fundamentales aparecen a menudo con muy distintas apariencias más o menos al mismo tiempo. La filtración adaptativa espacia presenta importantes analogías con algunos problemas bastante similares de la visiión artficial (robótica) que intenta inferir un mundo tridimensional a partir de una imagen bidimensional. De hecho, la imagen bidimensional por si sola no contiene suficente información como para hacer inferencias precisas. Se necesita algo más, algún tipo de "instrucciones" que están a menudo relacionadas con el hecho de que las cosas próximas entro sí tienden a parecerse más que las cosas alejadas -¡una idea de naturaleza enteramente geográfica!.
Tanto en la filtración adaptativa espacial como en la visión artificial surgen problemas de identificación de configuraciones. Por ejemplo, cuando realizamos una búsqueda secuencial del conjunto mejor (óptimo) de factores amortiguadores (µk) estamos buscando en realidad la mejor configuración que minimiza la desvación. De un modo similar cuando nos encontramos con un pico de población o de casos de SIDA muy elevado, tenemos que reconocer un "salto" en nuestra superficie, lo que es otra forma de identificación de configuraciones Nuestra filtración adaptativa espacial debe tener algún modo de superar estos problemas con las discontinuiades añadiendo características especiales (como la ponderacion inversa de las estimaciones de condados adyacentes o la búsqueda del mejor subconjunto de condados predictores), en un modo muy similar a como la visión artificial debe añadir unos requisitos técnicos extra entre la simple grabación de una imagen y su interpretacrón final.
La geografía tiene muchas perspectivas, cada una de ellas capaz de iluminar algún aspecto de nuestro maravilloso y complejo mundo fisico y humano. Aquí, al adoptar la perspectiva espacial, la perspectiva que engloba la dinámica, configuración, y estructura espaciales, y al centrarla en el problema tan general de la predicción del mapa siguiente, de la siguiente configuración espacial, vemos como los geógrafos piden ayuda a otros estudiosos que trabajan en epidemiología, intetigencia artificial y visión robótica, y quizás en otros muchos campos que se entfrentan a problemas similares. Los tiempos de la demarcación de fronteras disciplinarias se han acabado, los días en que nos preguntábamos "¿Pero esto es geografía?" han pasado. Nuestra existencia humana en el tiempo y en el espacio, no separados, sino siempre juntos, significa que se requiere tanto la perspectiva geográfica como la histórica si lo que realmente nos importa es llegar a comprender. De manera bastante poco común, la filtración adaptativa espacial y el rastreo paramétrico son geografía e historia combinadas, son enfoques que nos permiten hacer predicciones con fines totalmente humanos.
Notas
1. "World Health
Global Statistics", AIDS, 4, 1 990, págs. 605 610.
2. Rvachev, L y Longiní, I.
“A Mathematical model for the global spread of influenza”, Mathematical
Sciences, 75 1985 pág. 322. Diseñado originalmente para la gripe, el modelo se
adaptó para al VIH, Flahault, J. y Valleron, A.: “The role of air transport in
the global spread of HIV infection”, Ms. París, 1989 pág. 15.
3. FrÆland, S., et al: `HIV-I infection in Norwegian Family before 197O', The Lancet, 8598,1988, págs. 1344-45.
4. Recogido en Shilts R.: And the Band played on (Nueva York: St. Martin's Press,1987) una “historia temprana de la epidemia de SIDA (sobre todo en Estados Unidos), y quizás uno de los mejores ejemplos de reportaje periodístico da asta siglo.
5. Gould, P.: The
Geographer at Work (London: Routledge, 1985), en particular las páginas
l84-185.
6. Hooper, E.: AIDS
epidemíc moves south through Africa, New Scientist 1724, 1990, pág. 22.
7. Múller, O., et al. «The
presentation of adult HIV-1 in Kampala hospitals, AIOS, 4,1990, págs 601-602.
8. El experto en geografía, entrenado durante toda su vida para documentar las declaraciones que se le hacen, se enfrenta aqui con un dilerna ético que sienten muy directamente los mejores periodistas En el trabajo humano, es éticamente responsable proteger a los informantes expertos que ponen su confianza en ti y piden que no se revele su identidad. Sólo la confianza y el juicio personal pueden contar aquí, como en cualquier otra área de la ciencia.
9. Jäger H et al:
“Prevention of transfusion associated HIV transmission in Kinshasa. Zaire: HIV
Screening is not enough”, AIDS, 4,1990, págs. 571-74.
10. Parte de este material
ha aparecido en Gould, P.: «Modelling the AIDS epidemic for educational
intervention”, en R. Ulack (ed.), AIDS and The Social Sciences (Lexington,KY:
University of Kentucky Press, 1990); y en Boundaries and barriers in
relation to the diffusion of AIDS, en D. Seiner. c. Jaeger y M. Nauser (eds.):
Person, Society, Environment: Fragments of Anti-Fraqmentary Views of the World
(Zurich: ETH, 1990).
11. ¿El suministro de un día en un país del tamaño de Nigeria?
12. Por ejemplo, si la probabilidad da identificar el VIH es de 0,999 y Se usan 200 unidades de sangre, el l-(0,999)200=0,18 o un 18 por cierto de posibilidad de contagio.
13. Washington, DC es predominantemente negro, y el estudio piloto propuesto fue interpretado por los políticos locales como una búsqueda de “chivos expiatorios”, pese al hecho de que el 25 por ciento de todos los casos da SIDA y el 35 por ciento de los usuarios de drogas intravenosas infectados con SIDA son negros en proporciones mucho mayores que el porcentaje en el total de la población.
14. Por ejemplo, los métodos
usados por Brookmeyer, R. Y Gail, M: Minimum size of the acquired
immunodeficiency syndrome (AIDS) epidemia in the United States, The Lancet. 6
de diciembre, l986 págs 1320-23; y Gail, M. and Brookmayer, H.:Methods for
Projecting course of acquired inmunodeficiency syndrome epidemic, Journal of
the National Cancer Institute. 80, 1988, págs. 909-911
15. Ver, por ejemplo, Gardner, L. y Brundage, J. Immunodeficiency virus infection epidemic in the United States. Annals of American Geographers, 79,1989, págs. 25-43.
16. En mi opinión, las fuerzas armadas de Estados Unidos se han comportado de un modo totalmente ético cor respecto a esta cuestión. Todos los miembros de las fuerzas armadas estadounidenses se someten a un test anual para detectar el VIH, y no se destina ninguna persona infectada fuera de los límites nacionales de Estados Unidos.
17. Keeling, R.: HIV in
American university populations. Conferencia en el Ritenour Health Center, Penn
State University, Marzo, 1989.
18. Gould, P. An open
letter to the Penn State Community. Penn State Research, 10, 1989, págs. 4-5.
19. Flora, J yThorenson,
R.: “Reducing the risk of AIDS in adolescents”. American Psychologist, 43, 1988,
gas, págs 965-970; Moeller, T. y Bachman, O. “Assessment of adolescents
at risk for HIV infection”. MedicalAspects of Human Sexuality 1988, pags.
20-32. Strunin, L y Hingson, R. Acquired immunodeficiency syndrome and
adolescentst knowledge, beliefs, attitudes and behavior”. Pediatrics, 79,1987,
págs. 825-28. Shafer, M. “High risk behavior during
adolescence", en Shinazi, R. y Nahmias, A. (eds). AIDS in Children,
Adolescents and Heterosexual Adults (Nueva York, Elsevier, 1988), págs. 329-34.
20. Wallace A. A synergism of plagues: ‘planned shrirkage contagious housing destruction and AIDS in the Bronx', Environmental Research,47,I988, págs 1-33; Wallace, R: “Implications of approximate linear growth in time of US and New York City AIDS cases: travelling waves of HIV infection on a low dimensional sociogeographic' Network’ (próxima publicación):Wallace, A. “Things fall apart: The AIDS epidemie in the Bronx', trabajo que será presentado en la reunión a la reunión anual de la American Association for the Advancement of Science, Washington, DC, Febrero1991.
21. Información verbal y personal de dos periodistas de una importante revista informativa semanal y una cadena nacional de televisión, Mayo y junio de 1990.
22. Todo ello será tratado en profundidad en Gould, P. The New Plague:
Geographic Consequences of theAIDS Epidemic (en preparación) el segundo liber
geographicus pro bono público de una serie que examina temas globales desde
una perspectiva geográfica. El
primero fue Fire in the Rain: The Democratic Consequences of Cernobyl
(Cambridge, The Polity Press, 1990; Baltimore: Johns Hopkins University Press,
1990).
23. En lengua inglesa, las investigaciones geográficas clásicas se remontan a John Graunt: Natural aud Panca Observauans Made Upon the Bills of Mortality (London: Thomas Roycroft, 1662), y continúan en el siglo XIX con el trabajo del Dr. John Snow sobre el cólera. Hoy hay una rica tradición de investigación y análisis en geografía médica.
24. Hagerstrard, T:
Innovation Diffusion as a Spatial Process(Chicago: University of Chicago Press, 1969)
25. Gould, P: “The geographic interpretation of eigen values", Transactions of the Institute of British Geographers, Invierno, 1967, págs. 53-86.
26. Por ejemplo, Illinois, California, Oregon, Washington y muchos otros.
27. Bowen, W. “AIDS in LA”, mapa publicado por el Departamento de Geografía,
California State
University, Northridge, 1989.
28. Bowen, W. "AIDS in LA 1983-89” mapa publicado por el Departamento de Geografía, California State University Northridge 1990.
29. Openshaw, S. Wymer, C.
Skinner, C. y Sforzi, F. “Empírical study of confidentiality risks in the
release of micro census data” (Newcastle Upon Tyne Center for urban and
regional Development studies 1989) mss. pag 10.
30. Gould, P. DiBiase, D. y Kabel, J. “The Diffusion of AIDS”, una cinta de video de 20 minutos hecha en colaboración con WPSX-TV University Park PA, 1989.
31. Gould, P. DiBiase, D. y Kabel, J. “Le SIDA: la carte animée comme
rhétorique cartographique appliquée",
Mappe-Monde 1, 190, p. 21-26.
32. Gould, P, Gorr, W. y
Casetti, E. Understanding and Predicting the AIDS Epidemic in Geographic Space
(University Park, PA: The Penn State-Carnegie Mellon Ohio State Consortium, 1988).
33 Aber, R., Adams,J.
yGould, P. Spatial Organization: The Geographer's View of the World
(Englewood Cliffs, NJ, Prentice Hall, 1971).
34 Casetti, E. “The dual expansion method: an application to evaluating the effects of population growth or development” IEFF Transactions on Systems; Many and Cybernetics, SMC-16, 1986, págs. 29-39; Foster; S. y Gorr, W. Forecasting the geographic distribution of primary core physicians: an application of spatial adaptive fíltering”, Proceedings of the Sixteenth Annual Pittsburg conference on Modelling and Simulation, abril, 1985, págs. 91-98. Foster, S. y Gorr, W. “ An adaptive filter for estimating spatial varying parameters: an application to modelling police hours spent in response to calls for service”. Management Service, 32, 1986 págs. 878-899.
© Copyright Peter
Gould y Joseph Kabel 1990
© Copyright Geocrítica, 1976

 1,0000
1,0000