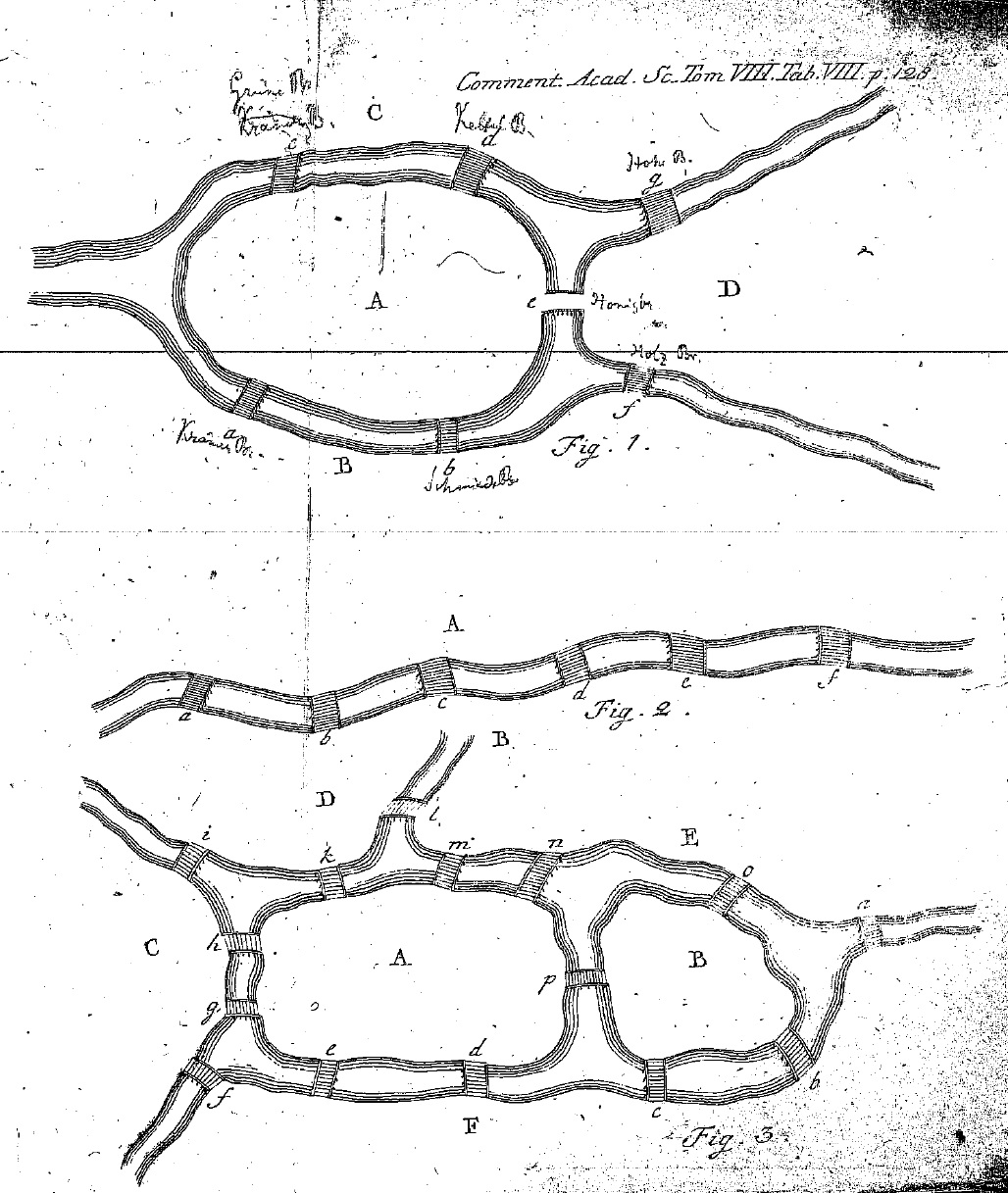
It is well known that mathematics are essencial for cartography. Less known the contribution of this last one to the mathematic development.  

An interesting example is the postulation of the Graph theory made by Leonhard Euler in 1735, when he faced to the problem of the seven bridges of Königsberg (currently Kaliningrad): how visit every district of the city without crossing more than once each bridge and coming back to the starting point. 

Inhabitants of the Prussian city debated this as an entertainment during their Sunday walks. Euler, however, was interested in the problem because he observed similarities to the theory called geometry situs, introduced by Leibnitz. From debating the problem, a general theory was developed. It was the first application of what today is known as topology: show that it can not be crossed each bridge once. 

See in My Mappy Place. It is well developed in Mathematical Association of America.

Illustrarion is from the original work of Euler: Solutio problematis ad geometriam situs pertinentis (1735).