És ben sabut que les matemàtiques són essencials per a la cartografia. Menys conegudes són les aportacions dels mapes al desenvolupament matemàtic.

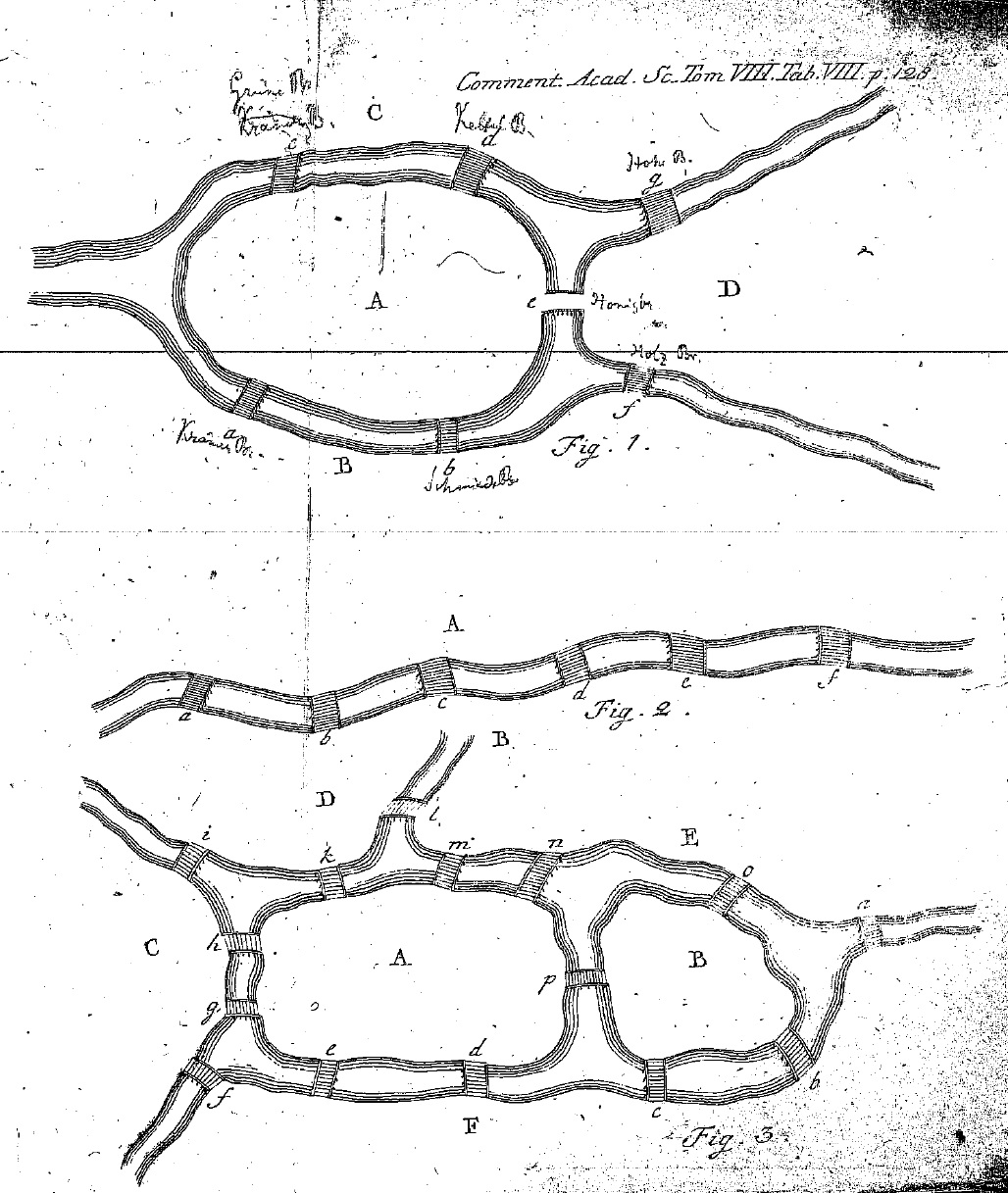
Un exemple interessant és el de la postulació de la teoria dels grafs que va fer Leonhard Euler al 1735, quan es va encarar amb el problema dels set ponts de Königsberg (actualment Kaliningrad): com visitar tots els districtes de la ciutat amb una passejada sense creuar més d’un cop cap dels ponts i tornant al punt inicial.

Els habitants de la ciutat prussiana ho discutien com un entreteniment durant les seves passejades dominicals. Euler, però, s’hi va interesar perquè hi va veure certes similituds amb la teoria anomenada geometria situs introduïda per Leibnitz. A partir de discutir el problema concret en va desenvolupar la teoria general. Va ser la primera aplicació práctica del que avui es coneix com la topologia: demostrar que no es podien creuar tots els ponts tan sols passant-hi una sola vegada.

Vist a My Mappy Place. Està ben desenvolupat al blog de la Mathematical Association of America.

La il·lustració és del treball original d’Euler: Solutio problematis ad geometriam situs pertinentis (1735).