Es bien sabido que las matemáticas son esenciales para la cartografía. Menos conocidas son las aportaciones de los mapas al desarrollo matemático. 

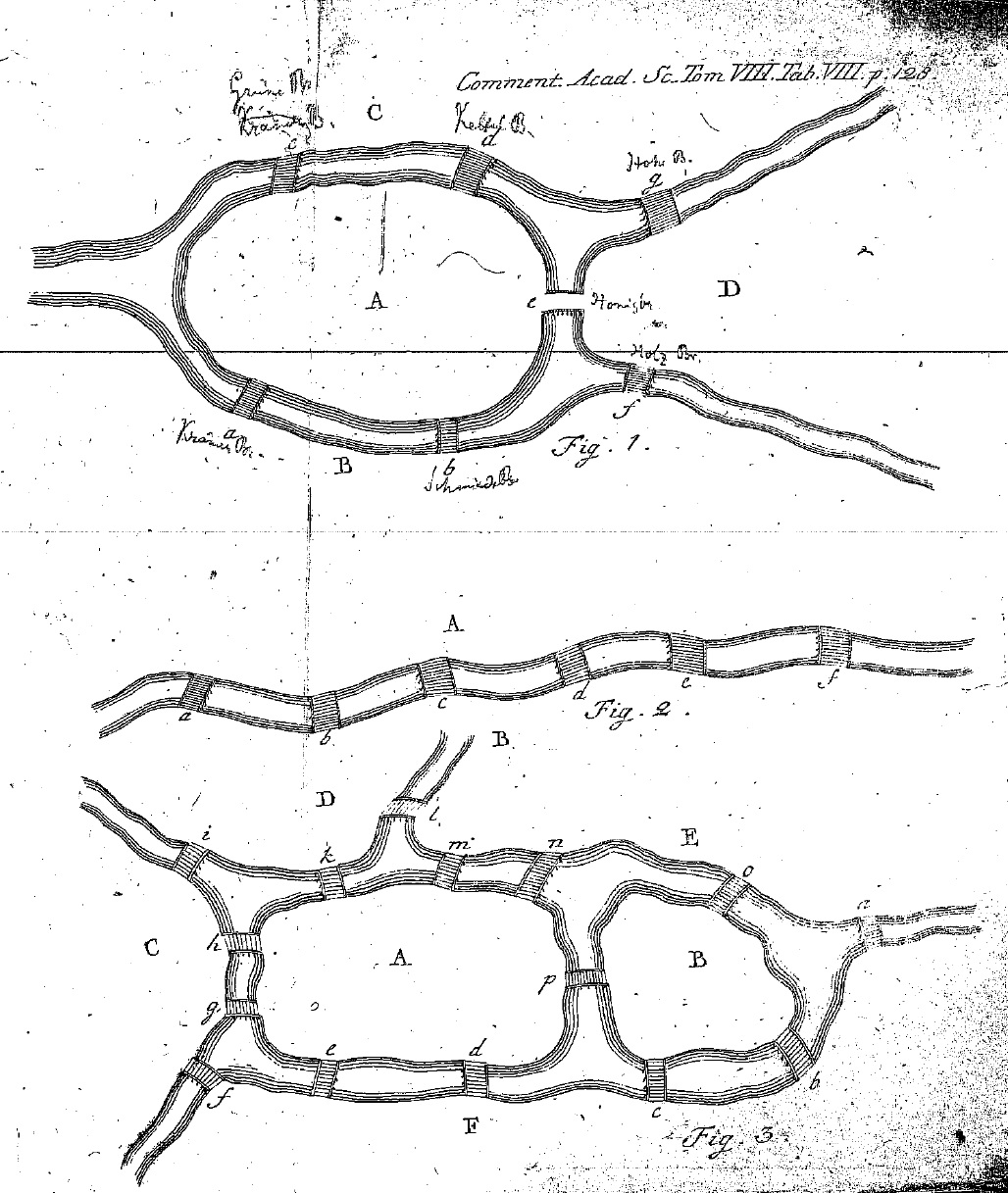
Un ejemplo interesante es el de la postulación de la teoría de los grafos que la hizo Leonhard Euler en 1735, cuando se enfrentó al problema de los siete puentes de Königsberg (actualmente Kaliningrad): como visitar todos los distritos de la ciudad con una paseo sin cruzar más de una vez los puentes y volviendo al punto inicial. 

Los habitantes de la ciudad prusiana lo discutían como un entretenimiento durante sus paseos dominicales. Euler, sin embargo, se interesó porque observó ciertas similitudes con la teoría llamada geometría situs introducida por Leibnitz. A partir de discutir el problema concreto, se desarrolló la teoría general. Fue la primera aplicación práctica de lo que hoy se conoce como topología: demostrar que no se podían cruzar todos los puentes tan sólo pasando una sola vez.  

Visto en My Mappy Place. Está bien desarrollado en el blog de la Mathematical Association of America.

La ilustración es del trabajo original de Euler: Solutio problematis ad geometriam situs pertinentis (1735).