  |
PROPORCIÓN POBLACIONAL 
En poblaciones dicotómicas con una proporción de éxitos
el estimador puntual del parámetro es la proporción muestral
de éxitos, p, que coincide con la media de la muestra cuando se
codifica como 1 la característica que se considera como éxito y 0 la
que se considera no éxito. A partir de un tamaño muestral
moderadamente grande el estadístico p tiene una distribución
aproximadamente normal. El intervalo de confianza para la proporción
poblacional está centrado en la proporción muestral; siendo sus
límites superior e inferior 
donde z
/2 es el valor crítico correspondiente al grado de
confianza 1- de la distribución normal tipificada y 
es el error típico de la proporción.
Para obtener el intervalo de confianza y contrastar hipótesis sobre la
proporción una alternativa consiste en tratar a la proporción como la media poblacional de una variable dicotómica codificada como se
ha descrito anteriormente (éxito=1, no éxito=0) y la secuencia es:
- Para el intervalo de confianza:
Analizar
Estadísticos Descriptivos
Explorar
- Para contrastar la hipótesis nula
Analizar
Comparar medias
Prueba T para una muestra
Utilizando este criterio los resultados numéricos no coinciden exactamente con los que se obtendrían aplicando la expresión del error típico de la proporción; no obstante la discrepancia es despreciable si el número de observaciones es suficientemente grande.
Otras alternativas para realizar este contraste son de naturaleza no paramétrica.
La prueba binomial prueba binomial analiza variables dicotómicas
y compara las frecuencias observadas en cada categoría con las que
cabría esperar según una distribución binomial de parámetro especificado en la hipótesis nula. El nivel de significación
crítico de esta prueba indica la probabilidad de obtener una
discrepancia igual o superior a la observada a partir de la muestra si la
distribución es la postulada por la hipótesis nula.
El nivel de significación crítico (bilateral) de este contraste debe interpretarse como:
el número de éxitos en la muestra.
Cuando n es suficientemente grande se calcula esta probabilidad aproximando la distribución binomial a la normal con corrección de continuidad.
La secuencia para realizar este contraste es:
Analizar
Pruebas no paramétrica
Binomial
Se especifica la variable en Contrastar variables. Se indica la proporción postulada en la hipótesis nula en Contrastar proporción. Si la variable es dicotómica se mantiene activada la opción Obtener de los datos. Si la variable no es dicotómica en Punto de corte se indica el valor de corte de forma que los inferiores o iguales se agrupan en la primera categoría y el resto en la otra.
El botón Opciones permite obtener estadísticos de resumen y
modificar el tratamiento de los valores missing.
PRUEBA CHI-CUADRADO
Otra alternativa de naturaleza no paramétrica se basa en el valor del
estadístico Chi-cuadrado. Esta prueba compara la frecuencia observada
para cada categoría (Oi) con la frecuencia teórica o esperada (Ei) bajo el supuesto de que la proporción de éxitos es la
postulada por la hipótesis nula. Para una muestra de tamaño n
la frecuencia esperada se calcula: 
para los éxitos y 
para los no éxitos. El estadístico de prueba
Chi-cuadrado se define 
y presenta una distribución Chi-cuadrado con 1 grado de libertad.
La secuencia es:
Analizar
Pruebas no paramétricas
Chi-cuadrado
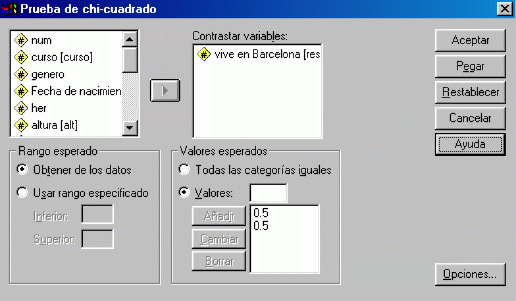
En el cuadro de diálogo se indica, en la casilla Contrastar
variables la variable sobre la que se realiza el contraste; obsérvese
que en Rango esperado está activada la opción Obtener
de los datos, que toma tantas categorías como valores distintos
presenta la variable. Si la hipótesis nula es 
los
valores esperados serán Todas las categorías iguales, en
cualquier otro caso se pueden introducir los valores (frecuencias esperadas
absolutas o relativas) con la opción Valores.
EJEMPLO
Con los datos de la encuesta Enctran.sav estimar la proporción de alumnos que viven en Barcelona mediante un intervalo de confianza del 90% y contrastar la hipótesis de que son mayoría.
El primer paso es comprobar si la variable Resid está correctamente
codificada, es decir, presenta valor 1 cuando el alumno es residente en
Barcelona y 0 en otro caso. En la base de datos se ve que la
codificación de la variable Resid no es la adecuada, por lo tanto, en
primer lugar habrá que recodificar la variable. La secuencia es Transformar > Recodificar > En la misma variable. En el cuadro de diálogo se selecciona la variable Resid y se definen los Valores antiguos y nuevos asignando al valor antiguo 2 el
valor nuevo 0. En el editor de datos se puede etiquetar el valor 0
como 'no' haciendo doble clic sobre el título de la variable Resid.
- Una aproximación del intervalo de confianza se obtiene con la secuencia Analizar > Estadísticos descriptivos > Explorar. En el cuadro de diálogo se selecciona como variable dependiente la variable Resid y en Estadísticos se modifica el grado de confianza fijándolo en el 90%. Los resultados que se obtienen al aceptar son:
Como se observa la media igual a 0,61 indica que el 61% de los elementos de
la muestra residen en Barcelona. A partir de esta estimación puntual de y de la estimación de su error típico se obtiene el intervalo
de confianza al 90% cuyo límites inferior y superior son 0,54 y 0,69,
respectivamente.
- Para contrastar las hipótesis
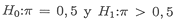considerando la proporción como media la secuencia es Analizar > Comparar medias > Prueba
T para una muestra. Se selecciona la variable Resid y se indica como
Valor de prueba 0,5, los resultados del contraste se recogen en el
siguiente cuadro:
Como el contraste es a una sola cola el nivel de significación
crítico es la mitad de 0,014, es decir, 0,007. Para niveles de
significación superiores a 0,007 se rechaza la hipótesis nula.
Así pues, para los niveles de significación habituales se acepta que
la mayoría de alumnos viven en Barcelona (>0,5).
- Utilizando la prueba binomial para contrastar las hipótesis 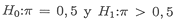la secuencia es Analizar > Pruebas no
paramétricas > Binomial.
Si la hipótesis nula es cierta, el número de residentes observado
(70) proviene de una población binomial de parámetros n=114 y =0,5 y por tanto con valor esperado 57. En tal caso:
Por lo tanto,
= 0,0095 que es el nivel de significación crítico del contraste a cola superior, en consecuencia se rechaza la hipótesis nula.
- Para contrastar las hipótesis 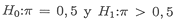aplicando la prueba Chi-cuadrado la secuencia es Analizar >
Pruebas no paramétricas > Chi-cuadrado.
Como el nivel de significación asintótico es 0,015 la hipótesis nula no se rechaza para los niveles de significación inferiores al 1,5 %.
|
|